面向物流提升裝備的桁架式立柱剛強度分析

薄澎濤，李 瑋，沈 婕

（1.西南林業大學 機械與交通學院，云南 昆明 650224；2.西南油氣田分公司 通信與信息技術中心重慶總站，四川 成都 610066）

0 引言

堆垛機是物流運輸中運載貨物的重要設備，立柱作為該設備的“承重墻”有著不可或缺的地位。堆垛機有單立柱和雙立柱兩種結構，其結構組成如圖1所示，現階段堆垛機的立柱形式普遍為封閉的腔體，中間穿插有帶孔的隔板。立柱的封閉腔體由金屬板材焊接而成，制造的形式決定了其有著安裝和拆卸不易、維修困難以及結構笨重的缺點。針對上述問題，本文提出了一種新型的桁架式立柱結構，相比于傳統的立柱結構，桁架結構具有凈空間值高、承受集中載荷效率高、空間擴展性強、設計靈活、易于組裝等優點[1]。在擁有這些優點的同時，桁架式立柱也要滿足剛度和強度的要求，因此，分析桁架式立柱剛強度對保證其安全性及動力學性能具有非常重要的作用。

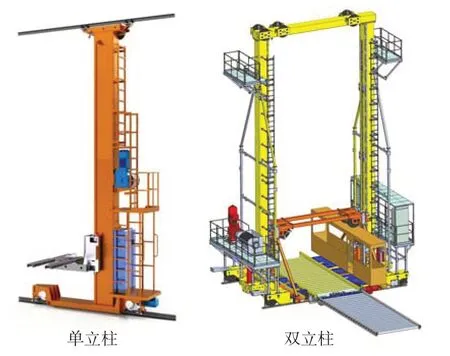
圖1 堆垛機

通過有限元分析研究桁架類的結構是一種較為普遍的方法。王春喜，等[2]針對穩定平臺測試實驗臺架，利用MSC軟件完成了桁架結構的建模和靜、動態特性的分析計算，驗證了該結構的輕微震動不影響設備的正常功能。陶友海[3]以黑木溝大橋為例，利用兩種軟件對掛籃進行數值模擬，分析了不同荷載下的剛強度，并對比了兩種軟件的適用性，得出了ABAQUS軟件更為合理的結論。文鐵軍，等[4]對桁架結構的通廊分析了風荷載作用于通廊的應力，并提出針對桁架類結構的設計建議。文獻[5-7]針對單立柱、雙立柱堆垛機的立柱和橫梁進行了力學模型的建立和剛強度分析,根據分析結果判斷了危險部位，通過給立柱加筋板，在立柱腹板兩側開孔，以及改變立柱的界面尺寸等3種設計，通過實驗的方式，對堆垛機結構進行了優化。上述文獻多是通過軟件作為有限元分析的手段和工具對桁架類結構進行分析，而在沒有有限元仿真軟件時如何通過理論計算驗證桁架類結構的剛強度并未過多涉及。

本文采用NASTRAN對桁架式立柱進行剛強度的有限元分析，驗證了其在幾種荷載作用下的撓度大小以及應力分布是否符合結構和材料的極限屈服強度。并基于經典小變形彎曲梁理論，探究在沒有有限元仿真軟件的情況下，為估算桁架式立柱結構承受荷載是否符合工程要求提供了相應的計算方法。

1 桁架式立柱的幾何模型

桁架式立柱由底板、頂板、立柱、拉桿以及前后彎折板等連接主體結構的零件組成。圖2所示，為桁架式立柱詳細的三維模型和各零件的位置關系，由于該模型的高度尺寸較大，中間的模型每層都相同，因此，為了更好地表達零件的細節，相同的模型只展示一部分。除立柱部分的材料采用了6063鋁型材外，其余部分均采用Q235B鋼材。

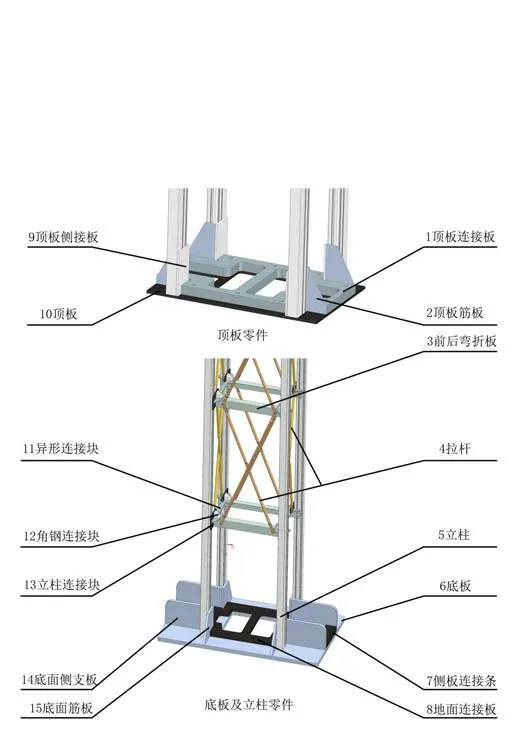
圖2 桁架式立柱零件圖

2 桁架式立柱有限元分析

有限元分析是一種計算數值的方法，用于確定物理系統的各種物理量，如位移、應力等。它主要基于有限元方法理論和數值解算技術，對復雜的物理現象進行精確的計算求解。有限元分析法在工程學領域應用廣泛，可以用于分析和優化各種工程結構、機械裝置和材料性質等。

2.1 模型簡化處理

有限元分析的簡化模型是指通過去除一些細節或者簡化復雜結構等方式，將原有的模型簡化而得到模型。簡化模型的目的是降低計算的復雜度和成本，同時要保證模型的準確性和可靠性。一般而言，在模型簡化并建立有限元模型時，應遵循等效剛度原則，即簡化后的模型和原模型在剛度上應基本保持一致[8]。也就是說，去掉模型中不顯著的項，通過減少項數使模型更容易使用，或者是減少模型的復雜度，使模型更容易計算。考慮到桁架立柱模型的上下底板為固定約束與載荷施加部位，該部位的模型圓角和小孔對剛強度分析幾乎沒有影響，因此，分析前在NASTRAN中對桁架式立柱模型進行簡化處理。

2.2 網格劃分

有限元分析的網格劃分是將連續的物理對象或區域離散化為一系列離散元素的過程。網格劃分是有限元分析中最重要的步驟之一，它直接影響到有限元分析的結果精度和計算效率，網格的劃分是有限元模型建立的基本要求。1D單元用于描述兩個節點之間直線或曲線結構的剛度，主要應用于梁、桁架、加強筋、網格連接等結構，表1列出了NASTRAN中部分1D單元的類型和用途。

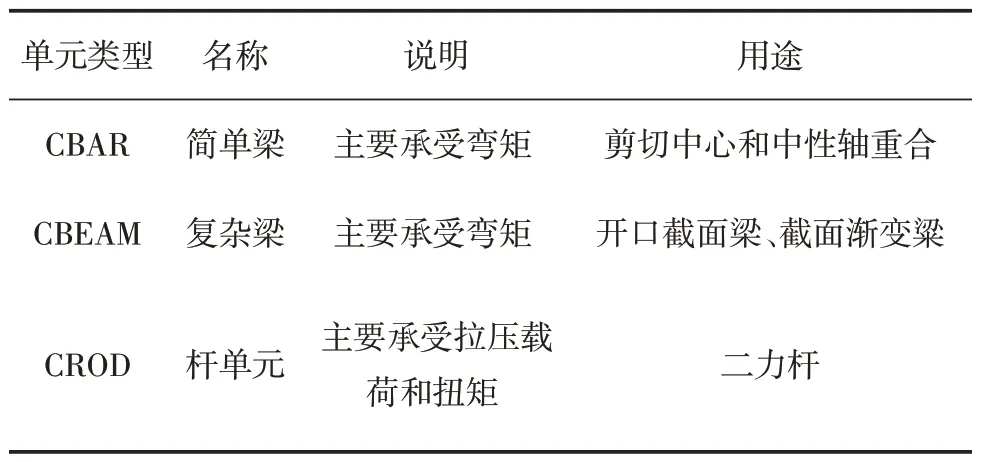
表1 1D單元的類型

模型立柱部分截面的剪切中心不與中性軸重合，因此采用復雜梁單元的CBEAM單元，在梁截面管理器中定義立柱截面。拉桿的截面需要根據不同的拉桿位置定義不同的截面，拉桿的兩端、中間部位、完整拉桿截面以及賦予3種截面的單根拉桿如圖3所示。

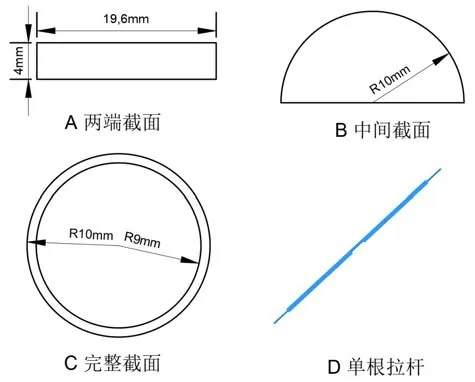
圖3 拉桿不同部位截面圖

2D單元也稱面單元，用于表示相對于其他維度單元厚度較小的一種結構。在桁架式立柱的前后彎折板、異形連接板和立柱連接塊3個零件部位，其模型的厚度遠小于長度和寬度，因此，將這三種零件抽取中面，并定義其厚度和材料，采用2D單元進行網格劃分來代替3D實體網格劃分，以減少后期網格數量和計算量[9]。除上述模型外，其余模型采用3D單元進行劃分，桁架式立柱模型零件均為規則的幾何模型，所以在劃分網格時，使用性能完善的自適應劃分網格,即系統根據模型的具體情況決定單元的大小進行網格劃分[10]。

劃分網格的過程中需要定義單元材料，表2為所用到的兩種材料的物理屬性。

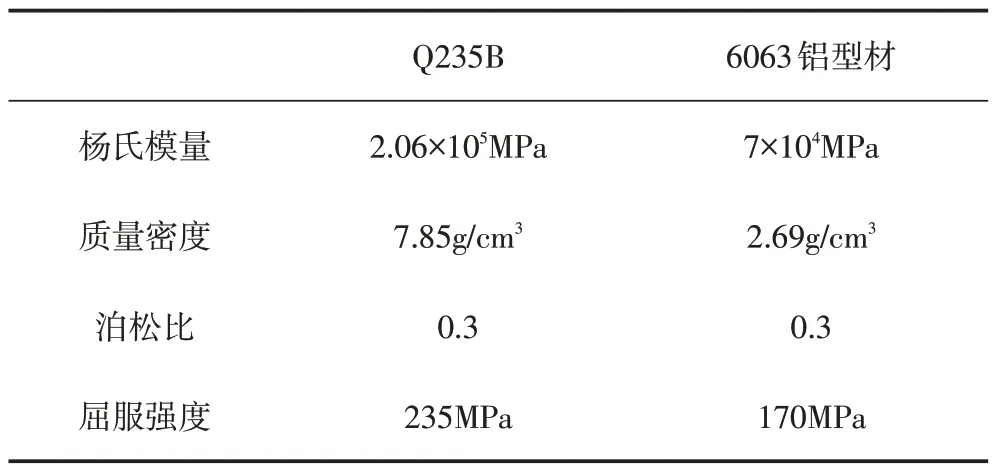
表2 材料物理屬性表

建立好的整體有限元模型如圖4所示，共產生了409 379 個單元和518 096 個節點，其中，1D 單元共有22 396 個，2D 單元共有106 055 個，3D 單元共有106 584個。通過單元質量的檢查，大部分單元的雅可比、寬高比、錐度、實體翹曲和邊點夾角等單元屬性都符合要求。桁架式立柱的高度有近2×104mm，模型中間重復的部分并沒有全部展示，并附上部分單元的細節局部放大圖。

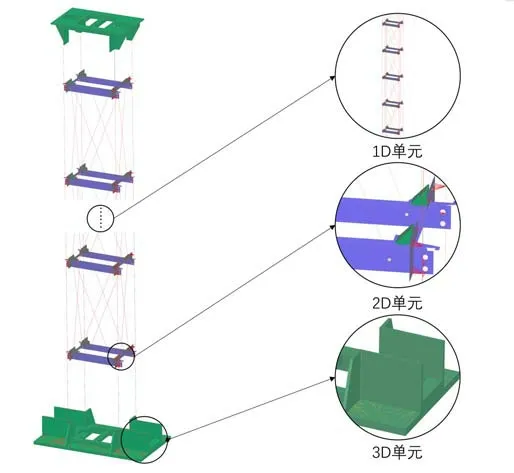
圖4 網格劃分結果和細節圖

2.3 連接關系和邊界條件

完成網格劃分后，各個零部件之間還需建立對應的連接關系，上下底板的零部件之間和立柱與底板之間為焊接，采用1D連接中的面-面方式即可實現零部件之間的焊接，需要注意的是立柱的1D連接所選擇的連接節點應全部處于立柱截面的形狀區域。桁架式立柱中間部分的連接主要以螺栓連接為主，由于立柱部分采用的是1D單元劃分的網格，立柱與中間零件的連接采用1D單元的節點與零件孔進行連接。螺栓孔之間采用RBE2單元蛛網連接。定義螺栓的連接中需要建立點到點、點到邊等節點連接，這些節點的選擇先后決定了其屬性為獨立節點還是依附節點，假設兩個孔之間的點到邊連接圓心點為獨立節點，孔邊節點為依附節點，而兩個圓心點在建立連接時則會產生圓心點既是獨立節點，也是依附節點的矛盾，如圖5所示，這就發生了節點的屬性沖突。若要解決這種沖突，須在解算方案的模型數據參數中將AUTOMPC更改為允許，這樣NASTRAN會根據模型情況自動判斷節點的獨立依附關系。

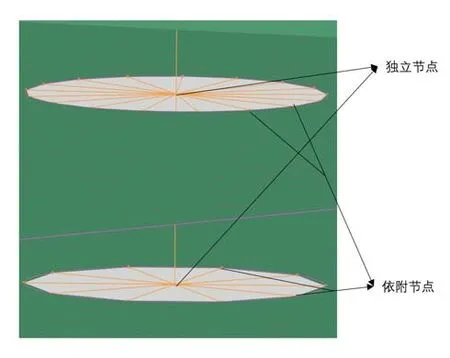
圖5 獨立節點和依附節點

完成有限元模型的建立后，根據桁架式立柱的實際工作需求定義邊界條件，創建包含4種工況的解算方案，表3為邊界條件施加的詳細情況。

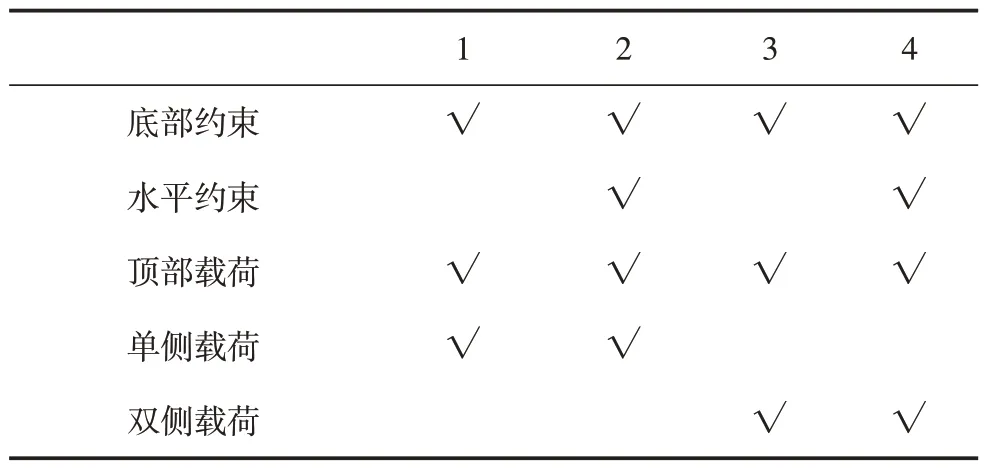
表3 邊界條件

圖6所示為4種工況的設定圖例：

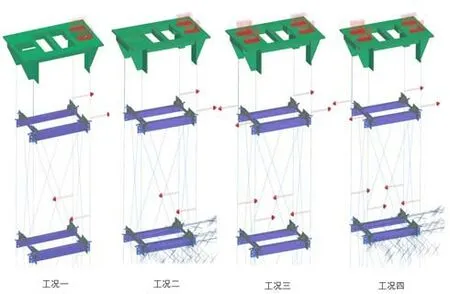
圖6 工況預設圖

工況一：固定立柱底部，頂部兩個130mm×49mm的長方形范圍內施加4 740N的力，方向豎直向下，在立柱內側距頂部600mm、1 400mm的位置施加一對方向相反的3 087N的力。

工況二：在工況一的基礎上，每間隔一組橫梁施加一個水平約束。

工況三：在工況一的基礎上，在對側對稱施加相同大小的力。

工況四：在工況三的基礎上，按照工況二對橫梁進行固定。

2.4 有限元分析結果

依據上述4種工況定義解算方案中的邊界條件并求解，得到4種工況下的應力云圖，如圖7所示。

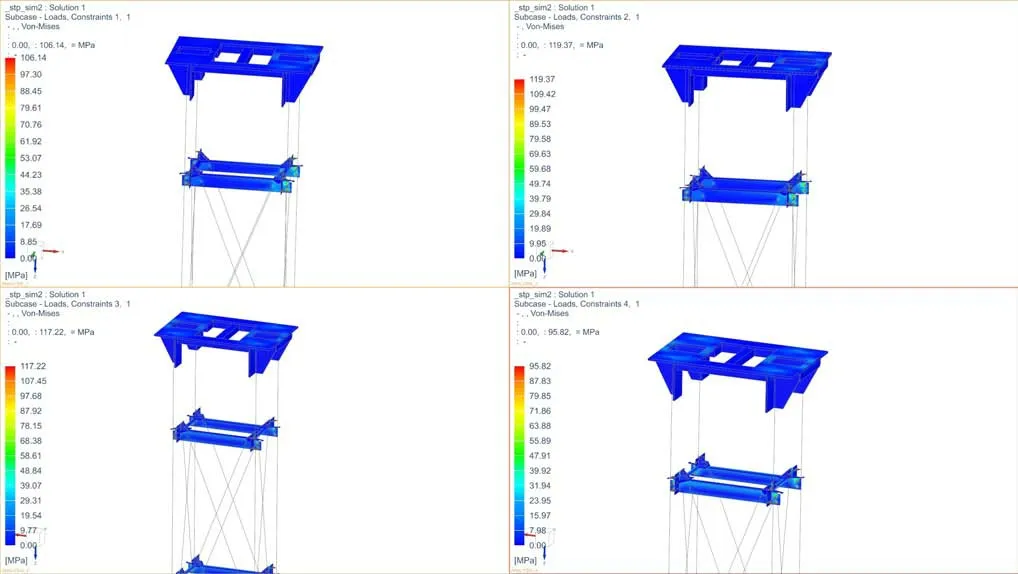
圖7 4種工況下的應力云圖

立柱部分的應力均取應力最大值，依據圣維南原理，如果把物體局部邊界上的力系，使用分布不同但靜力等效（主矢相等繞任一點的主矩也相等）的力系來代替，則這種等效處理使得物體的應力分布僅在作用區域附近有顯著影響，而在遠離作用區域的地方所受到的影響很小，可以忽略不計[11]。因此，為得到正確的應力值，立柱截面取一半高度的位置，即l=9 821mm。立柱截面的應力云圖如圖8所示。

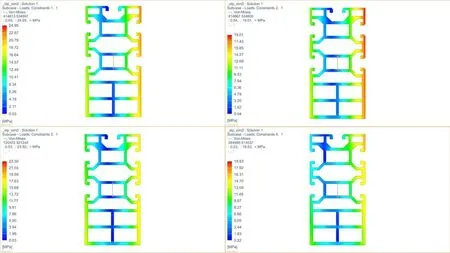
圖8 4種工況下立柱截面的應力云圖

4種工況下桁架式立柱所產生的最大應力都小于兩種材料的許用應力，滿足實際工作中的使用要求，表4為4種工況下的應力對比情況。

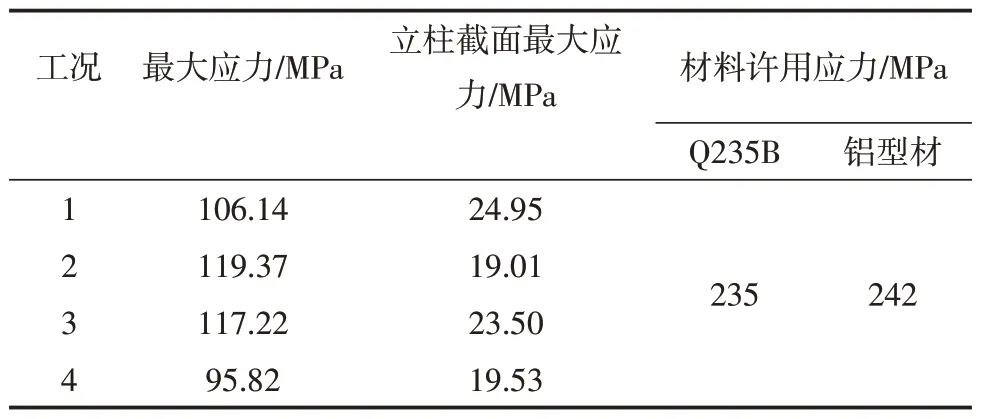
表4 四種工況應力對比

3 基于經典小變形彎曲梁的計算

3.1 整體截面抗彎剛度的確定

慣性矩是一個幾何量，通常被用作描述截面抵抗彎曲的性質。桁架式立柱的立柱截面為復雜截面，若要計算整體的撓度就需要計算桁架式立柱整體截面的慣性矩，4根立柱的截面一致，在得出單個復雜截面的慣性矩后，可以通過移軸定理得出4個截面關于整體模型中性軸的慣性矩。

整體立柱模型截面形狀及尺寸關系如圖9所示。

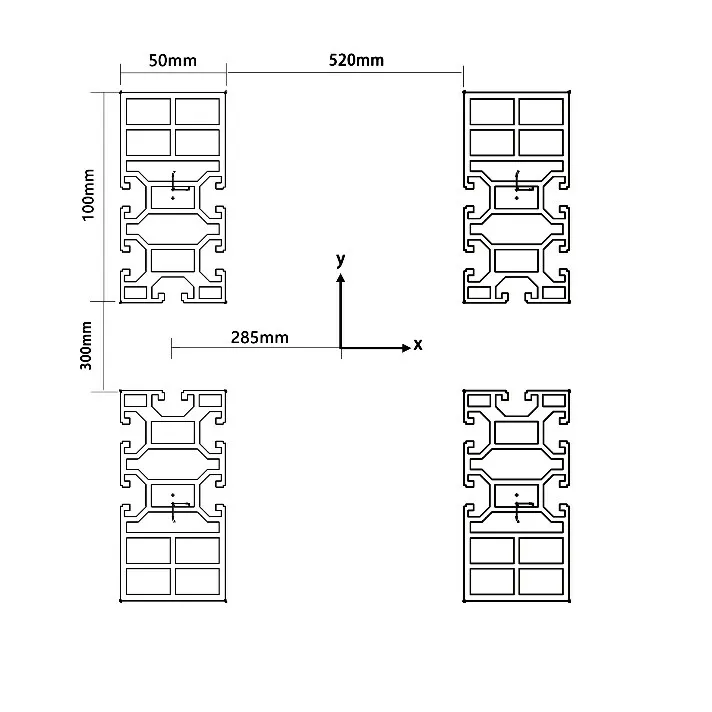
圖9 整體截面圖

由于立柱截面的形狀復雜，其面積計算起來較為復雜，因此，可以通過軟件直接得出此截面的面積及慣性矩Iyc，本文直接采用軟件內所給出的準確數據。

在得到單一截面對其中性軸的慣性矩之后，通過平行軸定理計算出每個截面對整體模型中性軸的慣性矩。查閱相關資料得到平行軸定理公式：

其中：Iy：截面對整體中性軸的慣性矩；

Iyc：截面對自身中性軸的慣性矩；

a：截面中性軸到整體中性軸的距離；

A：立柱復雜截面的面積。

代入數據可得：

Iy=4.47×105+2852×1 666.45=1.36×108mm4

則模型總的慣性矩為：

I總=4×Iy=5.44×108mm4

材料的楊氏模量E 在表2 中已給出，E=7×104MPa，桁架式立柱的整體抗彎剛度為：

EI總=7×104×5.44×108=3.8×1013MPa·mm4

3.2 桁架式立柱的撓度與應力

3.2.1 最大撓度。撓度是在受力或非均勻溫度變化時，桿件軸線在垂直于軸線方向的線位移或板殼中面在垂直于中面方向的線位移。本文所述的桁架式立柱的立柱部分為一等截面體，即EI為一定值。根據作用于立柱上的邊界條件，可以將桁架式立柱看作為一端固定，另一端施加荷載的懸臂梁，如圖10所示。

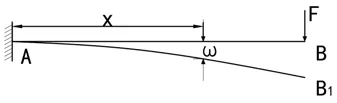
圖10 桁架式立柱等效圖

上述懸臂梁的彎矩與曲率關系為：

曲率又可表示為：

這里略去了式（3）曲率表達式中分母的高階項，因此，該理論只適用于小變形彎曲梁，聯立式（2）和式（3），得到撓曲線近似微分方程為：

對上式進行兩次積分，得：

其中x處的彎矩方程為：

由于A處施加了固定約束，在A截面處，桁架式立柱的撓度為0，代入式（5）中得到C=0，D=0。因此，桁架式立柱的撓曲線方程為：

桁架式立柱在力的施加處取得撓度的最大值，即x=l=19 642mm。將桁架式立柱的各項數據帶入式（7）中即可計算出端點B處的最大撓度fmax的值為：

3.2.2 最大應力。通過查閱相關資料[12]得到立柱彎曲正應力求解公式為：

將數據代入式（8）中得到立柱截面的應力為：

4 分析結果對比

在桁架式立柱頂端的側面施加一大小為3 000N的橫向力，底面施加固定約束，忽略重力，模擬懸臂梁理論計算模型，得到仿真計算結果。有限元仿真的撓度和應力結果如圖11所示。

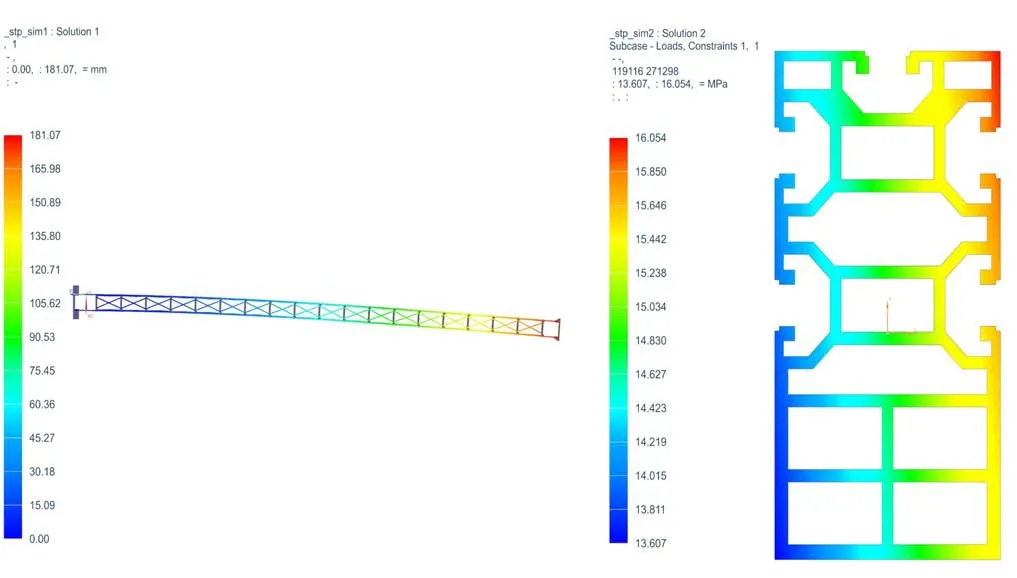
圖11 仿真結果

在頂端3 000N 橫向力的作用下，桁架式立柱最大的撓度為181.07mm，相較于理論計算結果199.42mm 有9.20%的誤差。立柱中間位置截面的應力理論值為16.79MPa，與仿真應力結果16.05MPa 相比有4.4%的誤差。

在上述理論計算過程中，并未考慮桁架式立柱的拉桿部分，拉桿部分的存在會增大桁架式立柱整體的抗彎剛度，這也是理論計算結果比仿真結果大的原因。若將拉桿截面的慣性矩為2 700.98mm4，代入式（1）計算得到拉桿截面對整體中性軸的慣性矩為：

Iy=2 700.98+2662×59.69=4.2×106mm4

拉桿的楊氏模量為E=2.06×105MPa，則拉桿部分總的抗彎剛度為：

4EIy=4×2.06×105×4.2×106=3.46×1012mm4·MPa

將其代入式（5）和式（6）中得到桁架式立柱的最大撓度和中間截面的應力分別為：

對比結果見表5。

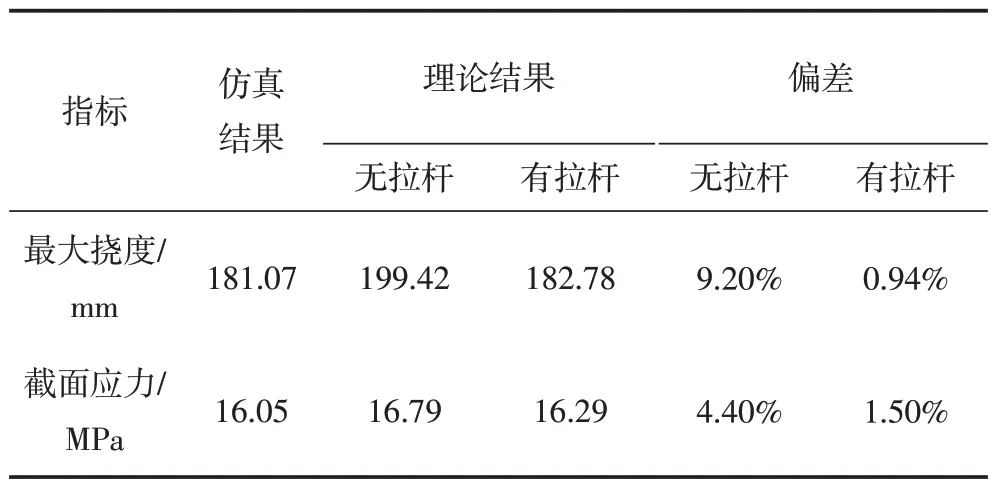
表5 理論與仿真結果對比表

綜上，在實際工程應用中，此類桁架式結構可以按照上述理論方法簡單驗證其在承受荷載時產生的變形是否符合工程需求，這為未能采用有限元仿真軟件時提供了一種行之有效的理論計算方法。

5 結語

本文主要以堆垛機為例，分析了物流提升裝備傳統立柱結構存在的一些問題，針對這些問題，提出了一種新型的桁架式結構。采用有限元分析方法，對桁架式立柱的整體結構進行了靜力學上的剛強度分析。在得到最大撓度和立柱截面應力的仿真數據后，基于經典小變形彎曲梁理論闡述了一種理論上的計算方法。在對比兩種方法得出的結果后，加入桁架的拉桿結構對整體剛度的影響，互相驗證了兩種方法的可行性，為桁架式立柱后續的設計與優化提供了參考。本文采用的研究方法對于其他類似產品部件的有限元分析也具有較好的借鑒意義。