基于創(chuàng)新型人才培養(yǎng)的“隨機過程”課程教學改革與實踐

孔慧華，史 娜，宋 妮，王 鵬

（中北大學數(shù)學學院 山西 太原 030051）

數(shù)學學科知識是各領域創(chuàng)新人才知識結(jié)構的重要組成部分。“隨機過程”作為一門研究隨時間變化的隨機現(xiàn)象統(tǒng)計規(guī)律性的數(shù)學學科，目前已在通信、控制、經(jīng)濟和管理等領域得到廣泛應用[1]。“隨機過程”課程的開設，有助于提高研究生的思維創(chuàng)造力、理論推導力以及研究和解決實際問題的能力。由于該課程的內(nèi)容知識抽象、理論性強，因此對數(shù)理基礎知識稍微薄弱的工科學生而言，將會出現(xiàn)無法把握該課程的基本理論知識與技能的問題，從而導致學生失去學習熱情。為了滿足我國創(chuàng)新型人才培養(yǎng)的需求，需要改變傳統(tǒng)的教師單向傳授、學生被動掌握的教學方法，建立促進學生全面發(fā)展、加強學生創(chuàng)新意識、增強學生創(chuàng)新實踐能力的新的教學方法。

如何通過“隨機過程”課程的教學激發(fā)研究生的創(chuàng)新意識、加強學生的創(chuàng)新應用能力，同時提高學生的學習效率，是“隨機過程”課程改革應該進行深思和研究的問題。下面將從三方面進行探討和分析。

1 激發(fā)學生的學習興趣、培養(yǎng)學生的創(chuàng)新意識

1.1 改革理論教學內(nèi)容

為了弱化“隨機過程”課程基礎理論性強和抽象難懂的特點，教師可在教學過程中介紹隨機過程的發(fā)展演變歷史、里程碑式的重大發(fā)現(xiàn)和與其相關的著名科學家的事跡。授課過程中可以引入隨機過程的奠基人柯爾莫哥洛夫的“隨機”人生，講解愛因斯坦、維納、萊維等人對布朗運動的開創(chuàng)性工作等。對于隨機過程中的重要概念——平穩(wěn)隨機過程、各態(tài)歷經(jīng)性、功率譜密度等，介紹它們的發(fā)展歷程、學術意義和應用價值。同時，可以根據(jù)不同背景學生的專業(yè)和培養(yǎng)要求，將隨機過程的課程內(nèi)容與各專業(yè)知識（經(jīng)管、信息、控制）相結(jié)合。

1.2 問題導向式教學模式

為了充分調(diào)動學生對課程學習的興趣，培養(yǎng)發(fā)展他們的實踐創(chuàng)新能力，可在課堂教學活動中，針對一些重要概念與理論，由教師提出問題并引導學生進行思考，最后讓學生探索這些概念與方法。例如講授平穩(wěn)過程各態(tài)歷經(jīng)性概念時，由教師提出問題“如何通過試驗近似求得平穩(wěn)過程的數(shù)學期望值呢？”引導學生思考“一種自然的方法是通過多次試驗得到多個樣本函數(shù)，用某個確定時間的試驗平均值去近似數(shù)學期望值。這需要多個樣本函數(shù)，然而，在工程技術中測量得到多個樣本函數(shù)往往很難。”繼續(xù)引導學生思考其他解決方案“充分考慮到平穩(wěn)過程的統(tǒng)計特性不隨時間推移而改變，那么能否通過一個樣本函數(shù)近似計算平穩(wěn)過程的數(shù)學期望和相關函數(shù)呢？”從而引出各態(tài)歷經(jīng)性概念。

問題導向式教學方式改變了“以講為主”的課堂形式，將學生的被動認知轉(zhuǎn)變?yōu)樽灾鲗W習，調(diào)動了學生的積極性和主動性，使他們在思考中獨立找到解決問題的研究方法。因此，在“隨機過程”課程中，教師根據(jù)講授內(nèi)容的特點，精心設計問題，可以激發(fā)學生對課程的學習興趣，有利于創(chuàng)新意識的培養(yǎng)。

2 理論與實際相結(jié)合，提高學生的創(chuàng)新實踐能力

2.1 課堂案例教學：理論聯(lián)系實際的橋梁

研究生學習數(shù)學的最終目的是使用數(shù)學，為了能夠使學生體會到運用所學理論知識解決具體問題的樂趣，提高其對理論的認識，教師在講述完隨機過程的重要概念和定理之后，通過案例教學將理論與實際聯(lián)系起來。如，在講解完馬爾科夫鏈的遍歷性定理和平穩(wěn)分布之后，為了提升學生對抽象理論的理解能力，提出下面的商品占有率問題。

案例：市場上甲、乙、丙三種型號的某品牌電風扇在四月份銷量相同。五月份甲型號保持原有客戶的60%，分別獲得乙、丙型號客戶的15%和30%；乙型號保持原有客戶的70%，各自獲得甲、丙型號客戶的10%和20%；丙型號保持原有客戶的50%，分別獲得甲、乙型號客戶的30%和15%。求五月份各型號電風扇的市場占有率及穩(wěn)定狀態(tài)時的市場占有率。

分析探討：由于占有率具有無后效性，故這三種型號的電風扇在各個月份的占有率構成了一個馬爾科夫鏈。由題目可知四月份各型號電風扇的占有率為1/3，同時獲取該馬氏鏈的一步轉(zhuǎn)移概率矩陣，從而得到五月份各型號電風扇的占有率。又由于這個有限狀態(tài)的馬爾科夫鏈滿足遍歷性定理，因此它的極限分布，即穩(wěn)定狀態(tài)時的占有率是存在的。

所以五月份各型號電風扇的占有率為

因為在一步轉(zhuǎn)移概率矩陣中，所有 =甲、乙、丙，故此馬氏鏈具有遍歷性。由遍歷性定理可知馬氏鏈的極限分布滿足

所以這三種型號電風扇的穩(wěn)定狀態(tài)占有率為（0.359，0.327，0.314）。

通過對該問題的分析探討和求解，學生對馬爾科夫鏈的一步轉(zhuǎn)移概率矩陣、遍歷性、平穩(wěn)分布等概念和定理有了更深刻的認識。諸如此類的案例還有很多，如在講授布朗運動過程時，可以介紹2021年諾貝爾物理學獎獲得者德國科學家哈塞爾曼的研究工作，他基于布朗運動理論，建立了隨機氣候?qū)W模型，并給出了尋求影響氣候主因的最優(yōu)指紋方法，從而能夠分辨出人類活動和自然界局部改變對氣候這一復雜系統(tǒng)的影響，真正實現(xiàn)學以致用。

“隨機過程”的案例教學作為理論與實踐的橋梁，可以讓學生感受到應用隨機過程理論知識處理現(xiàn)實問題的樂趣，深化對概念的認識，更好地服務于應用創(chuàng)新。

2.2 Matlab仿真教學：提高科學計算能力的重要手段

由于“隨機過程”課程的基本概念比較抽象，使用Matlab軟件模擬泊松過程、布朗運動和隨機游動等，可以使學生更易于掌握隨機過程的樣本函數(shù)、狀態(tài)這一類抽象性的基本概念，也能夠更有效地幫助他們對隨機過程教學中涉及的基本概念與理論建立起感性的理解，進而提高教學效果。下面以泊松過程為例給出其模擬過程。

設Xn服從參數(shù)為的指數(shù)分布，表示第n次和第n+1次事件發(fā)生的時間間隔，記

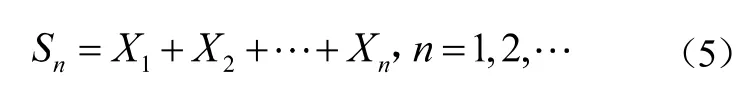
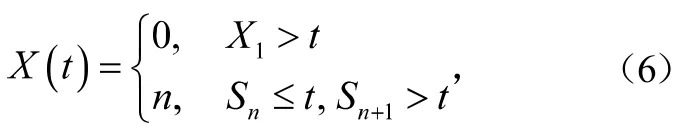
繪制（Sn，n）曲線即可獲得泊松過程的一次實現(xiàn)，如圖1所示。

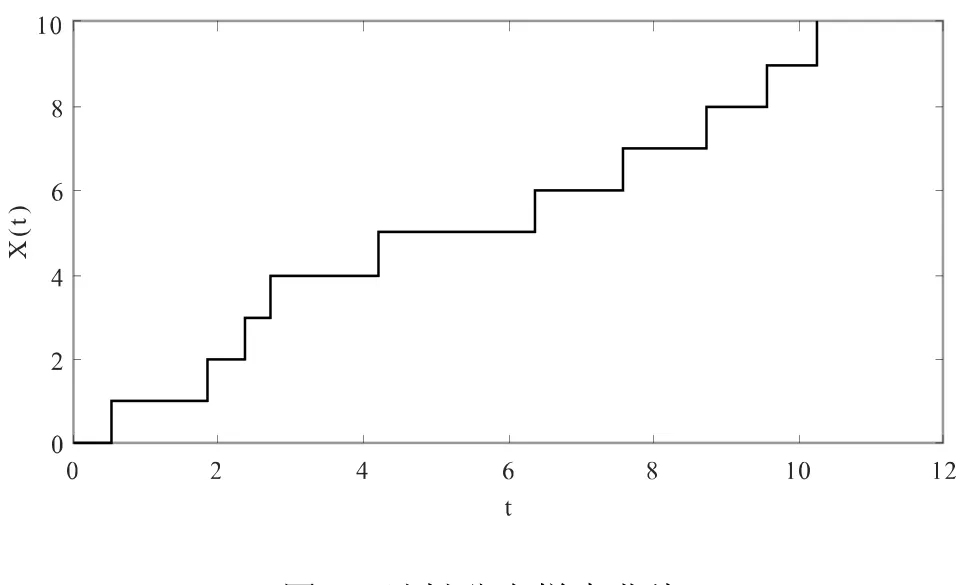
圖1 泊松分布樣本曲線

借助Matlab軟件編寫簡單的程序，抽象難懂的知識也可以轉(zhuǎn)換成簡單直觀的圖像，更生動易懂[2]。同時，利用Matlab軟件還可以解決隨機過程中很多問題復雜計算的求解，減少手工計算，增強學生基本的算法編寫能力，使其感受課程的趣味與應用價值。

2.3 教學與科研相結(jié)合，開展實踐性教學

教學和科研的完美結(jié)合是人才培養(yǎng)的重要手段和發(fā)展趨勢。因此，在介紹每類隨機過程的形成背景、定義原理和研究方法之后，根據(jù)教學內(nèi)容科學合理選取相關課題，為學生進行科學研究提供思路，引導其逐步走上科研道路。如，在學習完平穩(wěn)時間序列線性模型及預測后，可以讓學生對股票的價格、城市的電力、房價或者GDP進行預測。要解決這些問題，學生首先需要獲取相關數(shù)據(jù)，建立模型，利用Matlab軟件對模型進行求解，最終獲取相關模型并得到預測數(shù)據(jù)。通過對相關科研課題的研究不僅能夠幫助學生加深對基礎知識的認識與理解，而且學生還能學會如何應用相關隨機過程知識分析實際問題并提供解決方案，同時也讓學生體會到Matlab軟件強大的計算能力。教學和科研相結(jié)合，可以從整體上全方位提升教學效果，最終達到培養(yǎng)學生科研能力和創(chuàng)新能力的目的。

3 提高學生的學習效率

3.1 促進教學科研型師資隊伍的培養(yǎng)

要想達到高水平的研究生教育，就需要有一支高水平的師資隊伍。授課教師在研究生的創(chuàng)新能力培養(yǎng)方面發(fā)揮著極其關鍵的作用。就“隨機過程”這門課程來說，要求任課教師具有較高的學科素養(yǎng)和科研水平，能夠形象地、淺顯易懂地將抽象的數(shù)學課程講解清楚，這勢必會引起學生對該課程的濃厚興趣[3]。因此，任課教師要不斷了解學科發(fā)展前沿，將最新科學研究成果轉(zhuǎn)化成課堂案例，為課堂教學不斷引入新理論、新方法。

3.2 利用網(wǎng)絡平臺，實現(xiàn)分層次教學

計算機信息技術與互聯(lián)網(wǎng)的廣泛應用，給課程教學帶來了前所未有的變化，利用網(wǎng)絡平臺學習通、云班課等介紹課程及相關領域的基本情況、教學信息等，并且為不同層次的學生準備了不同的輔助教學內(nèi)容。

A層次：著重提高課堂質(zhì)量，牢固掌握所學知識。針對這部分同學，將授課的視頻、PPT課件和實際案例放在平臺上，供學生課后復習。同時在網(wǎng)上設立測試系統(tǒng)，并提供課程的相關試題。

B層次：具有良好的數(shù)學基礎，并且有志于從事科學研究和技術開發(fā)。針對這部分學生，在完成基本教學的基礎上，進一步拓寬、加深某些數(shù)學內(nèi)容，使學生能深入地掌握理論知識和數(shù)學思維。同時將與課程密切相關的論文與科研課題放在平臺上，供學生閱讀及深層次思考。

線上平臺是傳統(tǒng)線下教學的有效補充方式，通過線上線下的有機結(jié)合，可以引導學生由表面學習到深度學習。最終目的是增強學生主動學習的意識，養(yǎng)成自主學習的習慣，加強學生學習的深度和有效性。

4 結(jié)論

論文提出的以培養(yǎng)學生創(chuàng)新能力為目的的“隨機過程”課程的教學模式改革與實踐，能夠充分調(diào)動學生的學習興趣，深化學生對抽象理論的認識，提高學生理論聯(lián)系實際的綜合能力，有助于改變傳統(tǒng)教學中“重基礎理論、輕實際應用”的教學現(xiàn)狀，以適應教育部對學生進行創(chuàng)新型、應用型人才培養(yǎng)的需要。