升力式航天器太陽同步凍結回歸軌道保持策略

金宇帆 王 壯 閆曉東

西北工業大學航天學院，西安 710072

0 引言

面對時敏目標的觀測需求，超低軌道飛行器具備快速發射入軌、高機動特性、更高分辨率的優勢[1]。太陽同步凍結回歸軌道，可以實現針對特定區域的對地觀測任務時，飛行器經過同一星下點光照特性和軌道高度相同，且經過一個回歸周期后星下點軌跡重復，能顯著提高觀測效果。根據上述優勢，需要設計一種近地點位于超低軌道高度甚至臨近空間的太陽同步凍結回歸軌道。

對于太陽同步凍結回歸軌道的設計與軌道保持策略的研究較少。文獻[2]中提出了基于切向單脈沖的最低燃耗軌道面內保持策略，策略有效使衛星星座跟蹤并捕獲太陽同步凍結軌道。文獻[3]中針對人工太陽同步軌道設計方法進行了研究，提出了利用施加連續推力調整升交點赤經實現太陽同步軌道的方法，能夠滿足太陽同步軌道的要求。文獻[4]中通過分析太陽同步回歸軌道的軌道根數和星下點經度/緯度的關系，推導了一組軌道根數的修正公式，結合迭代修正，得到一組嚴格回歸的軌道根數。該軌道能夠重訪空間目標點，具有較高的回歸精度。

運行于超低軌道的飛行器，受地球非球形引力和大氣阻力攝動影響，其軌道高度會迅速衰減，為了延長飛行器在軌飛行壽命，需要研究有效的軌道保持方法。文獻[5]針對低軌星座在軌運行的高精度構型保持問題,提出了一種基于極限環的高精度相位保持方法，設定參考軌道，經數值仿真驗證，相位保持方法能夠在衛星定軌數據精度不高、數據采樣間隔較大的情況下,實現低軌星座系統的高精度相位保持。文獻[6]采用以軌道根數為基礎的控制方法，針對超低軌道飛行器使用離子推進器保持軌道進行仿真，驗證了離子推進器對超低軌道飛行器高精度軌道保持的有效性。可見現有研究主要聚焦于應用化學推力或電推力實施軌道保持控制，一般將氣動力作為阻力攝動，沒有考慮氣動升力對于軌道保持的作用。事實上，對于具有一定升阻比的升力式航天器而言，氣動升力可在近地點位于臨近空間的太陽同步凍結回歸軌道保持過程中發揮重要作用，這也將是本文研究的方向。

氣動力輔助變軌技術(AOT)是由London在1962年提出的概念[7]。姬聰云針對微小衛星氣動力輔助變軌過程，研究分析了在變軌過程中不同的近地點高度對優化效果的影響[8]，結果表明，氣動力變軌節省燃料能力隨近地點高度的降低而變強，但飛行器所受的過載、駐點熱流和動壓也越大。左光研究了類X-37B飛行器的氣動力輔助異面變軌性能，計算了變軌所需的燃料消耗量和軌道傾角改變量，并與采用沖量變軌方式的燃料消耗量進行了比較[9]，結果表明氣動力輔助變軌節省燃料的能力會隨著軌道傾角改變量增大而變強。可見目前針對氣動力輔助變軌技術的研究集中在以燃料最省為目的的軌跡優化問題，未針對利用氣動力輔助變軌技術實現例如太陽同步軌道或凍結軌道等特殊軌道的方法研究，而本文將針對這些問題進行研究分析。

軌道優化理論方面的研究興起于20世紀三、四十年代，主要應用于航天器設計優化領域。遲進梓等針對連續小推力航天器軌道轉移制導問題，將衛星變軌過程轉化為兩點邊值問題，并引入混合遺傳算法，結果表明該方法對小推力航天器變軌過程具有良好的優化效果[10]。張亞鋒等研究了Gauss偽譜法在有限推力軌道轉移優化問題中的應用，選取能量最優為性能指標，計算了同面和異面軌道轉移過程，驗證了Gauss偽譜法對于軌道轉移優化問題的適用性[11]。本文也將借助Gauss偽譜法求解多段連續軌跡優化問題。

1 軌道保持問題模型

1.1 軌道保持動力學模型

為了分析飛行器稀薄大氣環境飛行狀態，需要建立飛行器稀薄大氣動力學模型。在建模過程中進行如下假設：

(1)飛行器被視為重心不變的質點；

(2)地球為扁球體，僅考慮J2帶諧項影響；

(3)大氣隨地球一起旋轉，相對地球保持靜止；

(4)在機動過程中側滑角不存在，僅依靠攻角與 傾側角改變氣動升力方向。

經推導整理建立如下飛行器位置坐標系下動力學微分方程組：

(1)

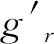
(2)

式中：α表示飛行器攻角，D和L分別表示飛行器所受氣動阻力和升力，計算公式如下：

(3)

式中：ρ表示大氣密度，CD和CL分別表示飛行器阻力系數和升力系數，Vr表示飛行器相對大氣速度，計算公式如下：

(4)

式(1)中gωe、g′r只考慮J2項時計算公式如下：

(5)

式中：J2=1.08263×10-3，μ為地球引力常數，Re為地球半徑。

在真空環境中飛行時，飛行器不受氣動力影響，依靠發動機推力調整軌道參數，將控制量設定為發動機推力大小和方向，對式(1)中部分方程進行調整：

(6)

式中：ux為本體系X軸控制分量，uy為本體系Y軸控制分量，uz為本體系Z軸控制分量，up為控制量平方和。

1.2 軌道要素與狀態量轉換關系

在研究過程中，需要在軌道要素數據與位置坐標系下狀態數據間進行變換，由位置坐標系下運動狀態計算軌道要素變換關系如下：

(7)

式中：a表示半長軸，r表示位置矢量，e表示偏心率矢量，Ω表示升交點赤經，i表示軌道傾角，ω表示近地點幅角，f表示真近點角，軌道根數示意圖如圖1所示。

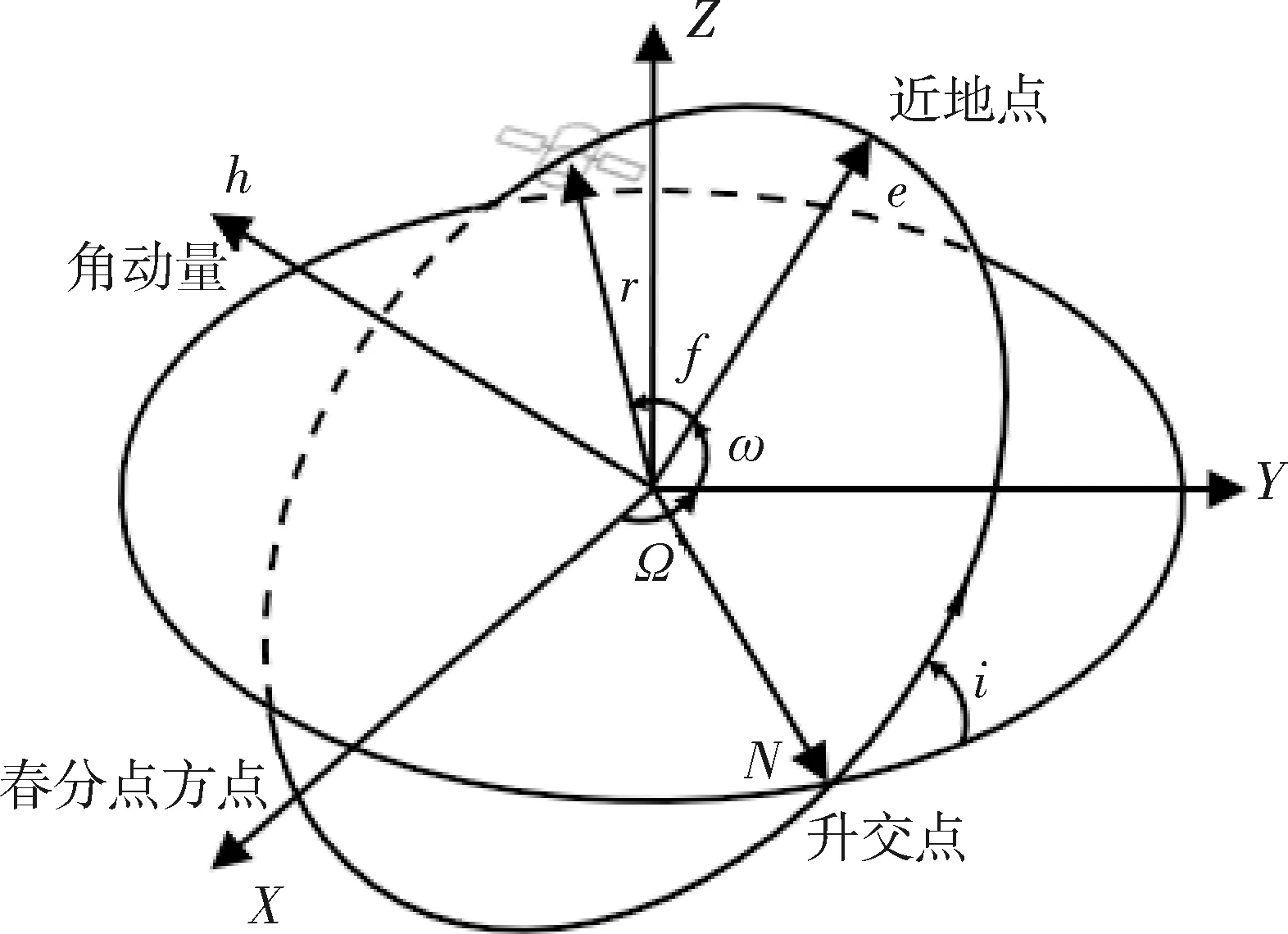
圖1 經典軌道根數示意圖

2 太陽同步凍結回歸軌道參數設計

飛行器位于太陽同步凍結回歸軌道時，在間隔回歸周期時間飛行至相同地區上空時太陽對地光照情況及飛行器對地觀測高度與上一回歸周期一致，在應對特定區域觀察任務時，設定合理的軌道參數，將軌道的近地點置于大氣層內，降低觀測高度，可以極大地提高飛行器對地偵察的觀測效果。

設計近地點經過大氣層的太陽同步凍結回歸軌道，需要綜合考慮地球自轉、地球非球形引力攝動及大氣攝動的影響，其中大氣攝動作為實現太陽同步凍結回歸軌道的控制量之一，在初始軌道參數設計中不予考慮，暫時忽略。

(8)

式中：TΩ為軌道周期，計算公式為：

(9)

回歸軌道滿足：

NΔθ=D×2π

(10)

式中：N為軌道回歸周期運行圈數，D為回歸周期。

對于地面時敏目標觀測任務，應盡可能縮短回歸周期，結合超低軌道飛行環境，設定飛行器回歸周期為1d，飛行器的軌道周期為1.5h，飛行器飛行16圈后完成回歸，由軌道周期計算公式(9)可以得到飛行器的軌道半長軸為6652.645km，設定軌道近地點高度為70km，則軌道遠地點高度為479km。

考慮太陽同步軌道設計要求。平太陽沿著赤道作周年視運動，經365.24422個平太陽日再次經過春分點，則平太陽在赤道上移動角速度為360/365.2422=0.9856(°)/d，則每個軌道周期移動角度為0.9856°/16=0.0616°。

在只考慮地球扁率J2項影響時，升交點赤經變化率[12]為：

(11)

由回歸軌道設定的軌道參數可以推導得到軌道傾角為96.5732°。

考慮凍結軌道設計要求。只考慮地球扁率J2項影響時，近地點輻角變化率為：

(12)

令近地點輻角變化率為0，可以推導得到軌道傾角為63.43°或116.57°。

綜合太陽同步軌道和凍結軌道受地球扁率J2項影響時的軌道傾角要求，為了節省軌道調整所需燃料，取兩者軌道傾角要求的中間值108°作為軌道傾角初值。

設某一區域為觀測區域，考慮近地點輻角受地球非球形引力攝動影響，存在沿逆行軌道運行方向后退的現象，設定軌道初始近地點輻角為50°，升交點赤經為280°，從遠地點開始飛行，則飛行器軌道初始參數設定如表1所示。

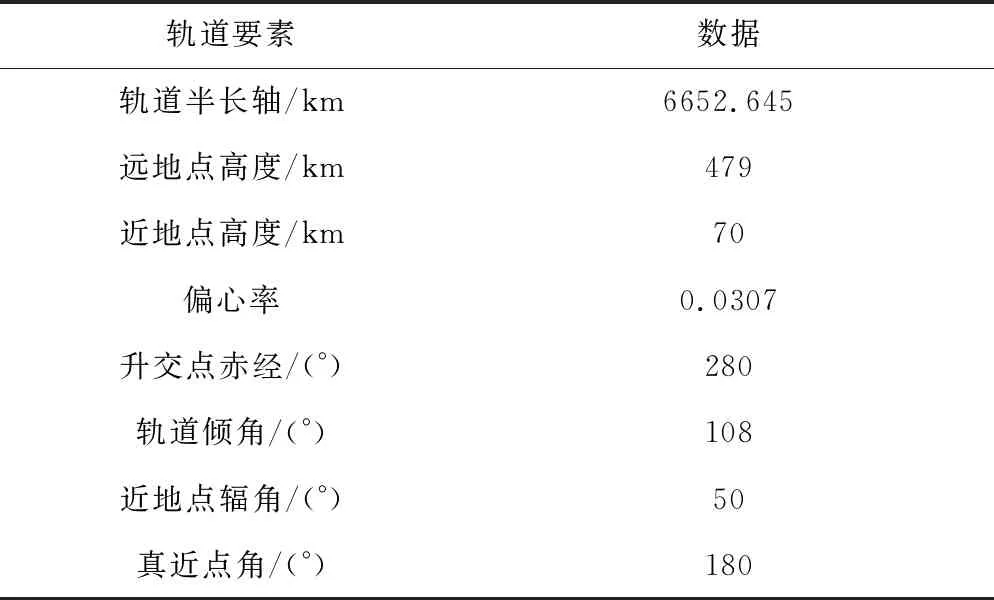
表1 軌道參數初值設定

3 太陽同步凍結回歸軌道保持策略和優化模型

3.1 太陽同步凍結回歸軌道保持策略

按照所設計的軌道參數，太陽同步凍結回歸軌道主要受地球非球形引力攝動和大氣攝動影響，軌道保持策略主要圍繞2方面設計：1)克服兩攝動項帶來的軌道面進動過量、軌道能量衰減及近地點輻角后退等負面影響；2)利用兩攝動項作用，控制軌道面進動量滿足太陽同步軌道升交點赤經進動量要求。據此設計單個太陽同步凍結回歸軌道周期三段式軌道保持策略：

(1)第一段為開普勒段，飛行器起始位于軌道的遠地點，按照設定的軌道參數自由飛行，期間不施加任何控制量，飛行高度到達大氣層邊緣高度時第一段結束；

(2)第二段為大氣層內飛行段，飛行器進入大氣層，調整飛行器攻角和傾側角控制飛行器氣動升力，微量調整飛行器升交點赤經進動量，躍出大氣層后第二段結束；

(3)第三段為動力調整段，飛行器躍出大氣層后飛向軌道遠地點過程，調整飛行器推力方向和大小，補充軌道能量同時調整飛行器近地點輻角，控制升交點赤經和軌道傾角，最終回到遠地點時除升交點赤經外其他軌道參數回歸初值，升交點赤經變化量滿足單個軌道周期太陽同步回歸軌道要求，完成整體軌道保持過程。

太陽同步凍結回歸軌道保持過程示意圖如圖2所示。

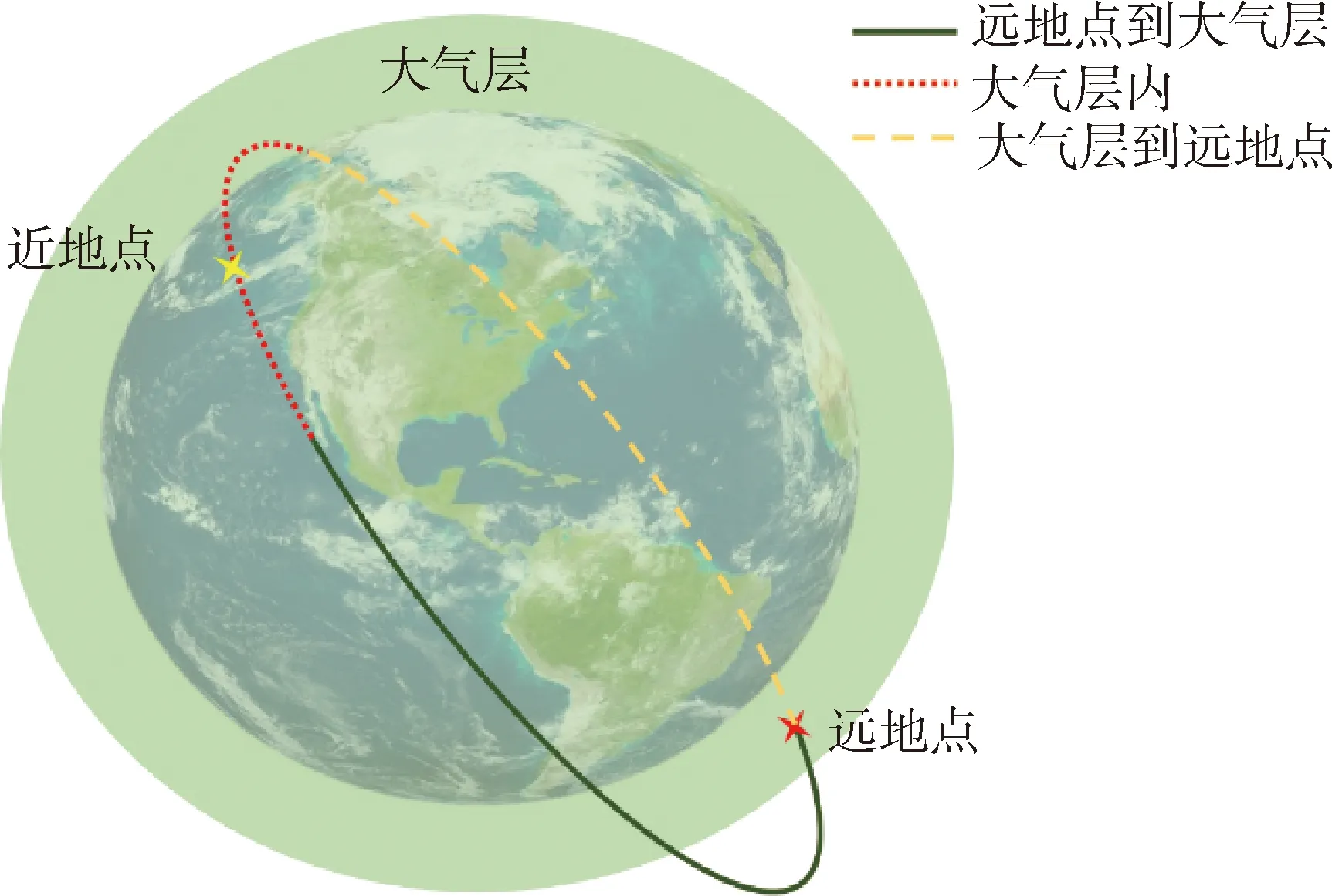
圖2 太陽同步凍結回歸軌道保持過程

3.2 太陽同步凍結回歸軌道保持優化模型

對于太陽同步凍結回歸軌道保持策略，最主要的任務就是保證飛行器在軌時間盡可能長，由此將軌道保持過程第二段和第三段歸結為以燃料最省為性能指標的軌跡優化問題，設置優化模型如下：

性能指標：

J=-mtf

(13)

(1)大氣層內飛行段：

優化變量約束：

(14)

狀態約束：

(15)

路徑約束：

(16)

(2)動力調整段：

優化變量約束：

(17)

狀態約束：

(18)

路徑約束：

upmin≤up≤upmax

(19)

優化問題的終端約束：

(20)

兩階段狀態量滿足內點約束：

(21)

式中：X(tfi)為各階段狀態量。

4 仿真驗證

4.1 飛行器模型與大氣模型

傳統衛星由于大多服務于較高軌道高度，在設計過程中很少考慮到自身的氣動特性，超低軌道氣動力輔助對于傳統衛星模型效果不佳，為了有效驗證氣動力輔助對超低軌道飛行器的作用，需要采用升力式飛行器模型進行仿真分析。

本文中采用CAV-H飛行器作為仿真驗證對象，其模型參數如表2所示。

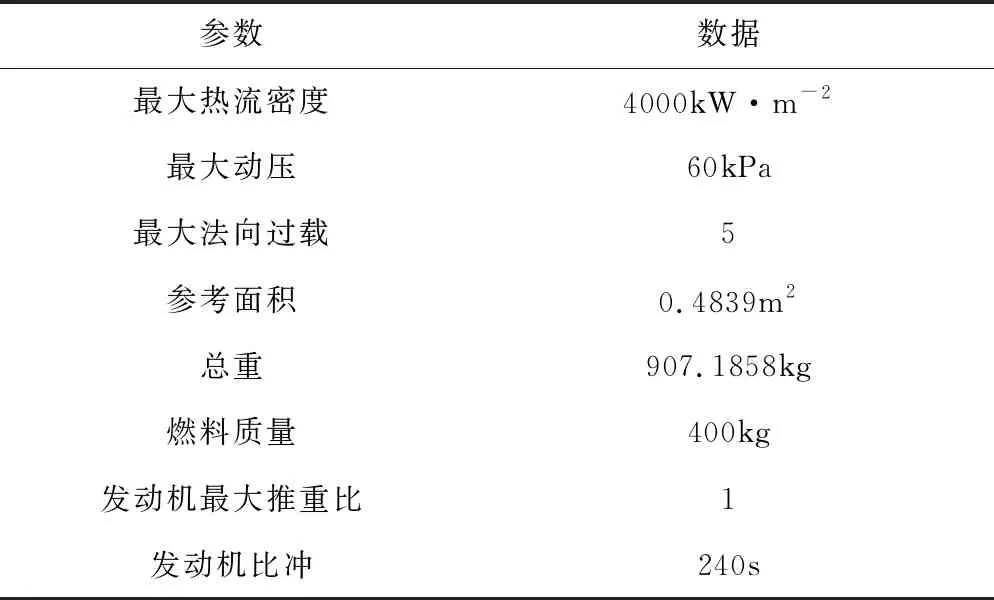
表2 CAV-H模型參數

氣動加熱模型為：

(22)

動壓模型為：

(23)

法向過載模型為：

(24)

位于超低軌道的飛行器飛行速度大多超過Ma23，所以只取用CAV-H飛行器Ma23氣動參數作為參考，為了提高優化效率，對氣動參數進行擬合估計，得到如下氣動參數計算公式：

(25)

其中,攻角單位為(°)，擬合后氣動參數數據如表3所示。

表3 氣動參數

在10°攻角情況下達到最大升阻比，在30°達到最大升力系數。

大氣模型采用美國標準大氣(US1976)，在本文中規定120km高度為大氣邊界高度。80km～120km高度大氣密度如圖3所示。

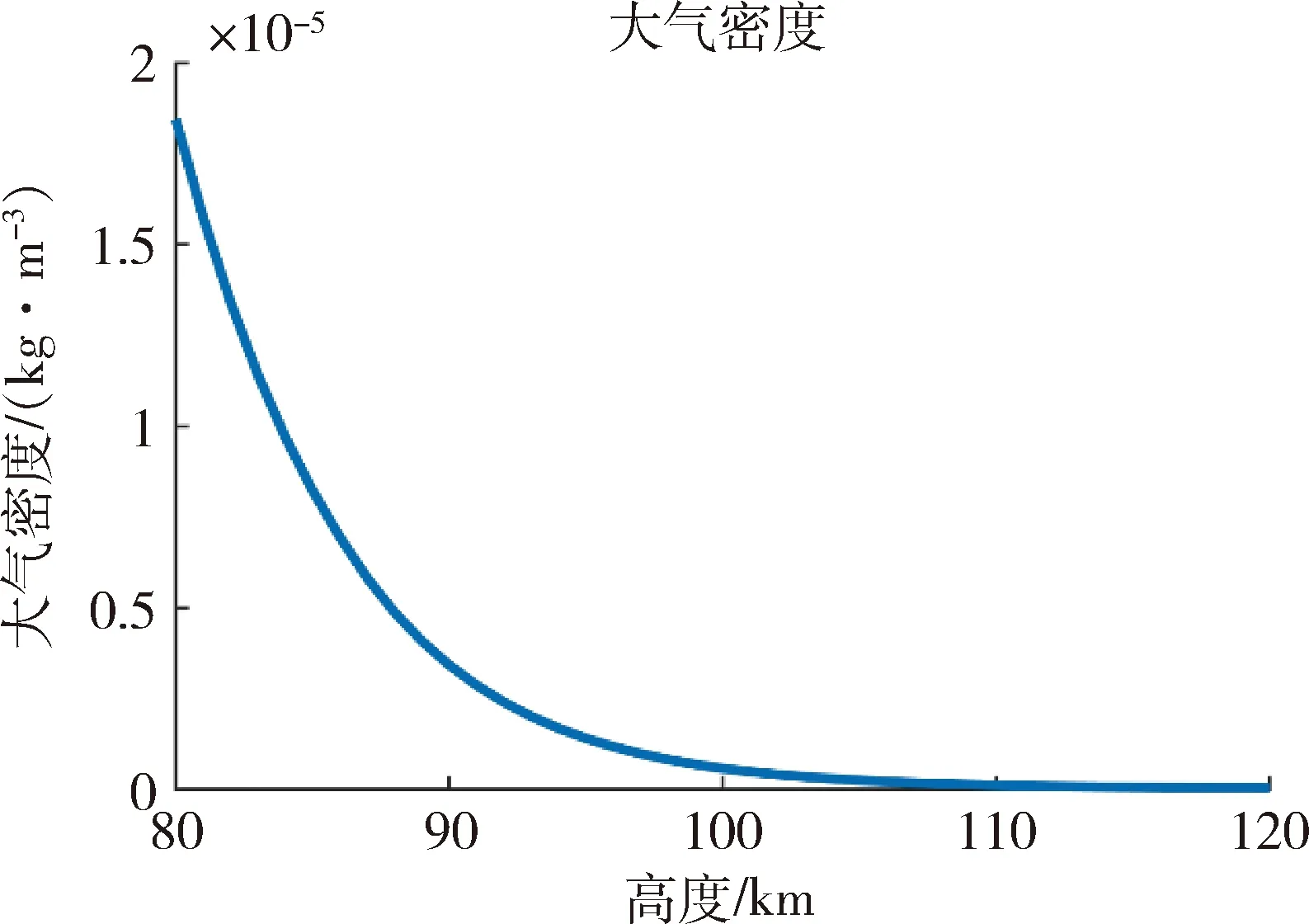
圖3 大氣密度

由圖3可以看到，大氣密度隨高度降低呈指數增長，80km軌道高度大氣密度高出120km軌道高度3個數量級。

4.2 策略有效性驗證

為了驗證策略的有效性，對表1設置的初始軌道參數，應用式(7)轉換為位置坐標系下初始狀態量，代入式(1)動力學模型，忽略其中動力項，進行開普勒飛行段積分計算，在到達大氣層邊緣時停止，得到表4所示再入大氣層初始狀態量。

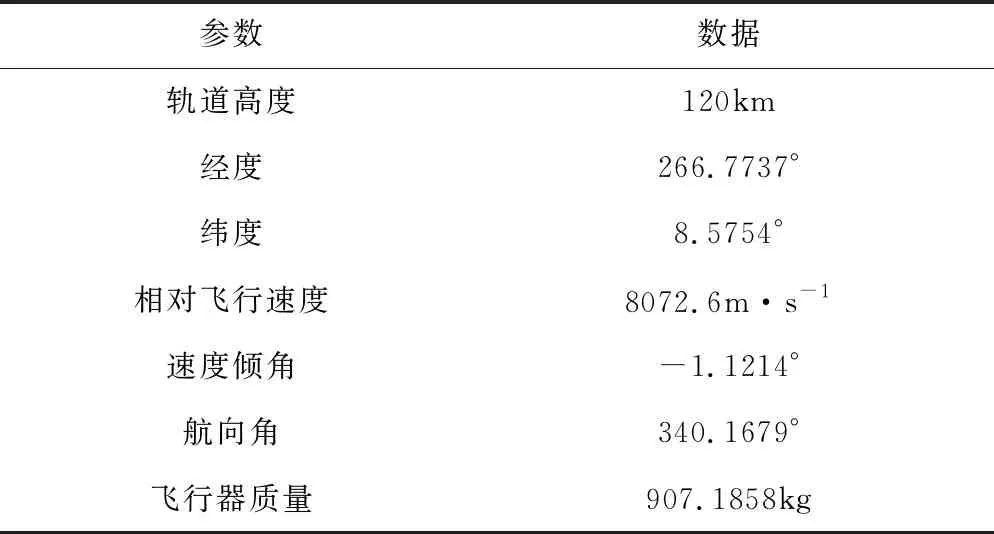
表4 再入大氣層初始狀態量

設置大氣層內飛行段優化變量約束及路徑約束如表5所示。設置動力調整段優化變量約束及路徑約束如表6所示，設置優化問題狀態約束如表7所示，設置優化問題終端約束如表8所示。

表5 大氣層內飛行段優化變量約束及路徑約束

表6 動力調整段優化變量約束及路徑約束

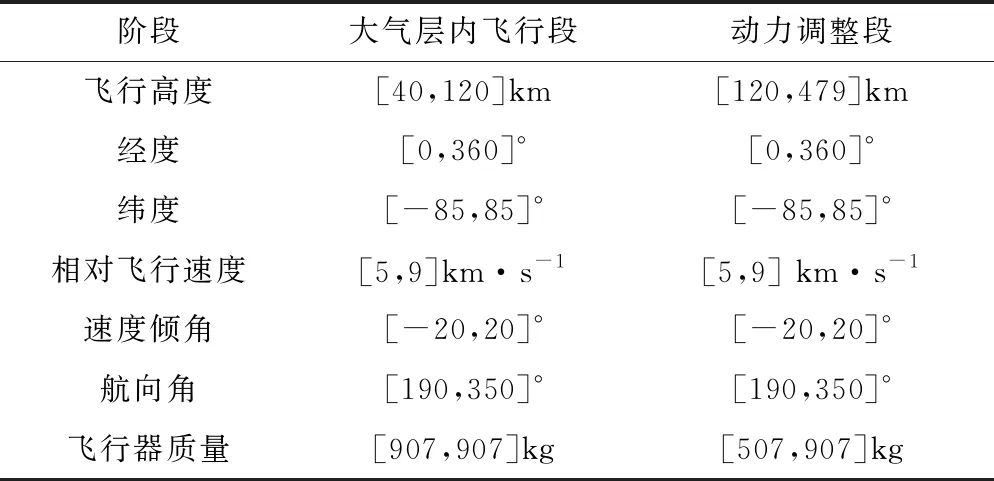
表7 狀態約束

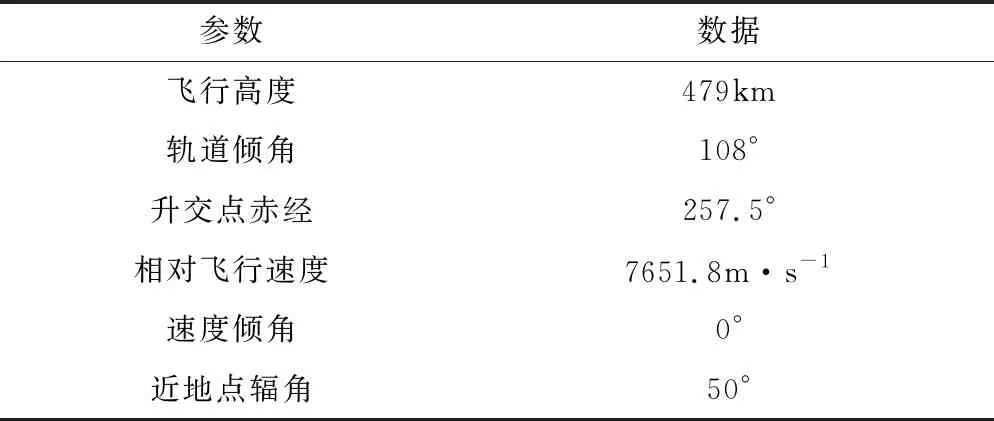
表8 終端約束

其中:升交點赤經通過式(26)計算而得：

ΔΩ=Ω0-ωeTΩ+0.9856°/16

(26)

采用高斯偽譜法和序列二次規劃算法對太陽同步凍結回歸軌道保持過程進行仿真分析，同時與相同初始軌道參數下不考慮大氣攝動、只考慮地球自轉及地球非球形引力攝動，不施加任何控制量時軌道參數變化情況進行對比，得到如表9和表10所示數據。

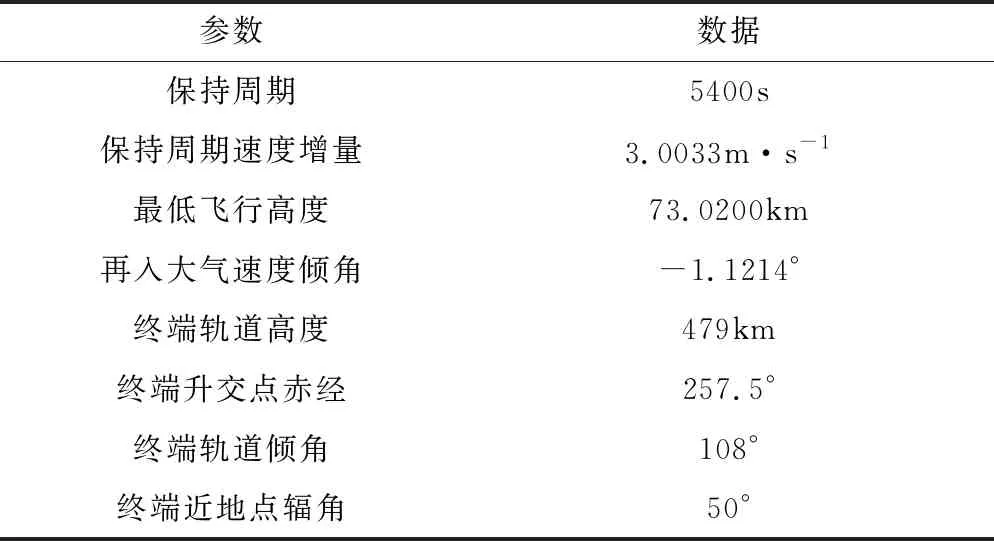
表9 軌道保持過程參數

表10 不考慮大氣攝動橢圓軌道參數

由表10可以看到，在無控不考慮大氣攝動情況下，在一個軌道周期內，軌道的升交點赤經進動量小于太陽同步軌道要求，近地點輻角沿飛行器飛行方向存在小幅后退，這是由于地球非球形引力攝動在當前軌道傾角大小下無法同時滿足太陽同步軌道和凍結軌道的要求，為實現太陽同步凍結回歸軌道必須對飛行器施加軌道控制。

由表9中數據可知，飛行器采用太陽同步凍結回歸軌道保持策略時，由于氣動力作用，飛行器軌道近地點高度由設計的70km提高到了73km，同時在單個軌道保持周期內，升交點赤經、近地點輻角滿足太陽同步凍結軌道的要求。軌道保持過程如圖4所示，為方便觀察升交點赤經受大氣攝動及地球非球形引力攝動影響的變化情況，在繪制升交點赤經變化過程時消除地球自轉帶來的升交點赤經變化。

由圖4中軌道保持過程可以看到，飛行器進入大氣層后，通過控制攻角與傾側角調整所受氣動力，小幅增大升交點赤經進動量以接近太陽同步軌道要求。在大氣層內近地點輻角受氣動阻力影響大幅后退，在動力調整段控制發動機開關以及推力方向，最終使飛行器滿足太陽同步凍結回歸軌道要求。

圖4 單次周期軌道保持過程

4.3 24小時軌道保持過程仿真分析

為更直觀觀察太陽同步凍結回歸軌道保持策略的有效性，采用單次周期軌道保持策略，同時連接16次軌道保持過程，對飛行器24小時太陽同步凍結回歸軌道保持過程進行仿真分析，得到如表11所示結果。

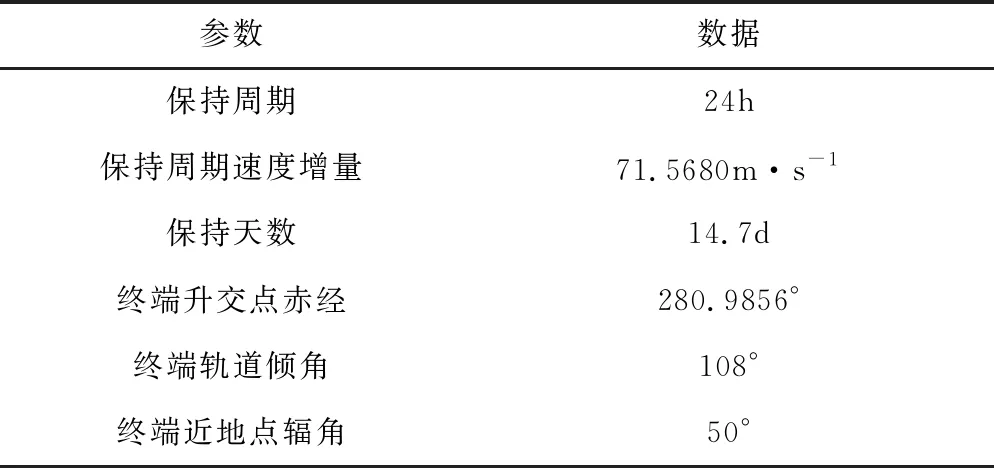
表11 24小時軌道保持過程參數

由表11數據可知，飛行器按照所設計的軌道保持策略，可實現14.7d的太陽同步凍結回歸軌道保持任務。經過24h飛行后升交點赤經增加0.9856°，近地點輻角和軌道傾角和初始值相同，滿足太陽同步凍結回歸軌道的要求。軌道保持過程如圖5所示。

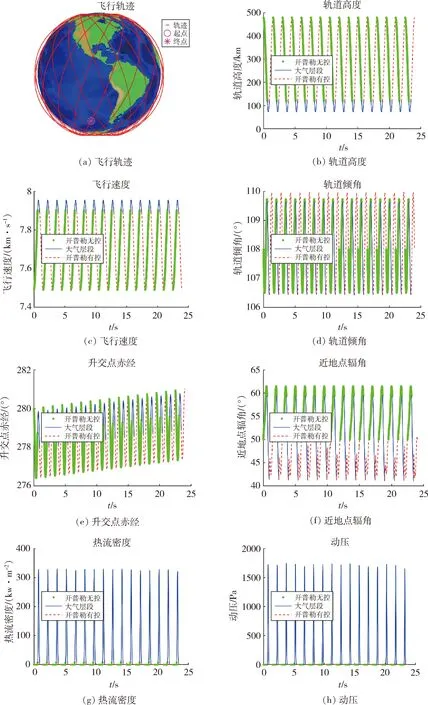
圖5 24小時軌道保持過程

由圖5(a)可以看到，飛行器經過24h飛行，星下點軌跡回歸到起始飛行點，滿足回歸軌道要求；由圖5(e)可以觀察到，升交點赤經呈緩慢增大狀態，單個軌道保持周期增大0.0616°，在24h軌道保持過程后最終增大0.9856°，滿足太陽同步軌道要求；由圖5(d)和(f)可以觀察到，近地點輻角和軌道傾角在單個軌道保持周期相同的時間大小相同，滿足凍結軌道要求；同時由圖5(g)和(h)可以看到，飛行器在大氣層內承受的峰值動壓和熱流都比較小，飛行包線具有可行性。

5 結論

本文以升力式飛行器為對象，以航天器對地偵察任務為需求，結合超低軌道飛行器對地觀測的優勢與升力式飛行器較強的機動能力，設計了一種近地點位于臨近空間的太陽同步凍結回歸軌道，并設計了氣動力結合發動機推力的軌道保持策略與優化方法。針對太陽同步凍結回歸軌道保持過程進行了飛行仿真和速度增量需求分析，結果表明：

1)通過設計合理的軌道傾角，利用地球非球形引力攝動，同時控制飛行器所受氣動力，飛行器可以滿足太陽同步軌道要求。若加以控制利用，兩者對于飛行器在軌運行具有積極影響；

2)結合氣動力與發動機推力的軌道保持策略，可以實現升力式飛行器14.7d的太陽同步凍結回歸軌道保持任務。