過(guò)驅(qū)動(dòng)衛(wèi)星姿態(tài)動(dòng)態(tài)控制分配研究

謝方圓 張愛(ài)民

1. 中國(guó)人民解放軍63766部隊(duì)，西雙版納 666200 2. 西安交通大學(xué)電子與信息學(xué)部，西安 710049

0 引言

衛(wèi)星運(yùn)行在復(fù)雜多變的太空環(huán)境中，不僅面臨來(lái)自外界的各類干擾影響，還可能由于外界或內(nèi)部的原因出現(xiàn)各種故障，進(jìn)而對(duì)功能造成影響。在衛(wèi)星在軌期間的各類故障中，執(zhí)行機(jī)構(gòu)發(fā)生故障的比例很高，而且對(duì)衛(wèi)星姿態(tài)造成的影響很大。為了提高衛(wèi)星對(duì)執(zhí)行機(jī)構(gòu)故障的容錯(cuò)能力，現(xiàn)代衛(wèi)星往往采用3個(gè)以上的反作用飛輪構(gòu)成冗余執(zhí)行機(jī)構(gòu)。那么一個(gè)控制需求會(huì)有多種可行的執(zhí)行機(jī)構(gòu)分配方案，這就引出了控制分配問(wèn)題。

針對(duì)過(guò)驅(qū)動(dòng)衛(wèi)星的控制分配問(wèn)題，傳統(tǒng)的偽逆分配法，其本質(zhì)上是固定分配，不能充分利用執(zhí)行器冗余的優(yōu)勢(shì)[1]。動(dòng)態(tài)控制分配(Dynamic Control Allocation, DAC)在故障時(shí)根據(jù)約束條件和最優(yōu)化目標(biāo)將虛擬控制力矩重新進(jìn)行分配，使執(zhí)行機(jī)構(gòu)最終輸出的控制力矩盡可能與虛擬控制力矩一致[2]。提高了控制過(guò)程的精確度、系統(tǒng)對(duì)執(zhí)行機(jī)構(gòu)故障的容錯(cuò)能力，進(jìn)而延長(zhǎng)衛(wèi)星在軌壽命。如文獻(xiàn)[3]中針對(duì)空天飛行器再入過(guò)程異類冗余執(zhí)行機(jī)構(gòu)的復(fù)合控制分配問(wèn)題，設(shè)計(jì)了基于二次規(guī)劃的按需動(dòng)態(tài)分配律，實(shí)現(xiàn)了姿態(tài)準(zhǔn)確跟蹤。文獻(xiàn)[4]在過(guò)驅(qū)動(dòng)衛(wèi)星姿態(tài)控制中應(yīng)用基于負(fù)載均衡的控制分配方法，優(yōu)化了推力分配布局，延長(zhǎng)了執(zhí)行機(jī)構(gòu)使用壽命。

相對(duì)于被動(dòng)容錯(cuò)方法，采用DAC可以無(wú)需設(shè)計(jì)過(guò)于復(fù)雜的控制器，以提供對(duì)飛輪故障的魯棒性，而是通過(guò)DAC方法進(jìn)行處理；相對(duì)于主動(dòng)容錯(cuò)方法，不需要重構(gòu)控制器[5]，也會(huì)相應(yīng)的使控制方法的設(shè)計(jì)復(fù)雜度降低。所以，將簡(jiǎn)單的控制器和DAC結(jié)合，是針對(duì)飛輪故障的一種有效的姿態(tài)控制設(shè)計(jì)方法。但在以往的文獻(xiàn)中，應(yīng)用動(dòng)態(tài)控制分配方法時(shí)，將權(quán)值矩陣對(duì)角線元素設(shè)置為最大限幅值倒數(shù)，并沒(méi)有將飛輪故障的影響考慮在內(nèi)。本文考慮飛輪故障，重新設(shè)計(jì)了對(duì)角權(quán)值矩陣的計(jì)算方法。

另外，無(wú)論何種執(zhí)行機(jī)構(gòu)，都存在由于物理限制存在輸出力矩和轉(zhuǎn)速的上限。在要求的力矩或轉(zhuǎn)速超過(guò)上限時(shí)，執(zhí)行機(jī)構(gòu)就無(wú)法跟隨控制命令，造成實(shí)際輸出的力矩和要求之間存在誤差，即執(zhí)行機(jī)構(gòu)發(fā)生了飽和。但一些文獻(xiàn)在設(shè)計(jì)控制律時(shí)并沒(méi)有考慮這一點(diǎn)。如文獻(xiàn)[6]中，僅設(shè)計(jì)了控制器，對(duì)于工程實(shí)踐中可能出現(xiàn)的執(zhí)行機(jī)構(gòu)飽和問(wèn)題沒(méi)有加以考慮，缺乏實(shí)踐指導(dǎo)意義。Kenneth提出了解決這一問(wèn)題的兩種方法[7]。其中利用控制效率矩陣(安裝矩陣)零空間特性的修正方法，可以使超出執(zhí)行機(jī)構(gòu)位置和速度限制的分配方案重新落入可行域內(nèi)，且保證控制矢量方向不變。

衛(wèi)星發(fā)射過(guò)程中，顛簸可能帶來(lái)結(jié)構(gòu)變形，現(xiàn)代快速響應(yīng)衛(wèi)星安裝矩陣在發(fā)射前可能來(lái)不及校準(zhǔn)，這些因素都會(huì)使衛(wèi)星不可避免的存在執(zhí)行機(jī)構(gòu)安裝偏差，往往會(huì)對(duì)控制精度有較大影響。所以高精度的姿態(tài)控制必須考慮執(zhí)行機(jī)構(gòu)存在安裝偏差的問(wèn)題[8-9]。

以上提及的衛(wèi)星姿態(tài)控制中可能出現(xiàn)的問(wèn)題，以往許多文獻(xiàn)中一般只著眼于它們中的一部分，而忽略了其他部分，沒(méi)有綜合考慮。雖然設(shè)計(jì)的控制方法對(duì)其他未考慮的問(wèn)題可能有一定的控制效果，但缺乏理論支撐和仿真驗(yàn)證。也有少量的文獻(xiàn)將以上問(wèn)題綜合考慮[10]，但控制器設(shè)計(jì)過(guò)程復(fù)雜，不利于實(shí)際工程應(yīng)用。

本文綜合考慮不確定干擾、飛輪安裝偏差、故障以及飽和，結(jié)合滑模控制和動(dòng)態(tài)控制分配，利用零空間法處理飛輪的飽和問(wèn)題。仿真結(jié)果證明，本文提出的控制方法對(duì)上述問(wèn)題有良好的控制效果。

1 衛(wèi)星姿態(tài)模型

1.1 衛(wèi)星姿態(tài)方程

采用四元數(shù)描述的衛(wèi)星姿態(tài)動(dòng)力與運(yùn)動(dòng)學(xué)方程為：

(1)

(2)

(3)

式中：J∈R3為衛(wèi)星慣量矩陣；we表示本體系Β相對(duì)于期望系Ο的誤差角速度；有

(4)

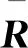
(5)

假設(shè)1.干擾力矩d有界，即滿足‖d‖≤λ。其中:‖·‖表示(·)的2-范數(shù)，λ>0為正常數(shù)。

假設(shè)2.角速度w和姿態(tài)四元數(shù)qv均可通過(guò)直接測(cè)量或間接計(jì)算得到。

1.2 飛輪結(jié)構(gòu)與故障分析

1.2.1 飛輪安裝偏差分析

記執(zhí)行機(jī)構(gòu)的數(shù)量為m>3，執(zhí)行機(jī)構(gòu)產(chǎn)生的力矩向量為v=[v1v2…vm]T。衛(wèi)星的控制力矩u=[u1u2…un]T(n=3)，由反作用飛輪通過(guò)安裝矩陣D提供：

un×1=Dn×mvm×1

(6)

考慮航天器反作用飛輪存在安裝偏差ΔD,設(shè)標(biāo)稱部分為D0,即有：

D=D0+ΔD

(7)

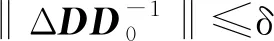
1.2.2 飛輪故障分析

飛輪效率矩陣為F=diag(f1,f2,…,fm),其中fi(i=1,2,…,m)∈[0,1]表示每個(gè)飛輪的故障系數(shù)，fi=1表示飛輪正常，fi∈(0,1)表示飛輪效率降低，fi=0表示完全失效。記vc為飛輪的輸入指令。飛輪實(shí)際輸出v的表達(dá)式如下：

v=Fvc

(8)

假設(shè)4.F已經(jīng)準(zhǔn)確檢測(cè)或估計(jì)到，其估計(jì)誤差本文不做討論。

1.2.3 飛輪飽和分析

定義飛輪在物理限制下可以輸出控制力矩的范圍為：vmin≤v≤vmax，速度的范圍為：ηmin≤η≤ηmax。設(shè)采樣時(shí)間為T,綜上，在某一時(shí)刻t飛輪輸出力矩范圍可表示為：

(9)

(10)

這使得位置和速率的雙重約束轉(zhuǎn)化為單位計(jì)算周期內(nèi)的位置約束問(wèn)題。

1.3 問(wèn)題陳述

綜上，本文研究的問(wèn)題可以描述為：在衛(wèi)星姿態(tài)控制過(guò)程中，考慮存在不確定干擾以及飛輪安裝偏差的情況下，當(dāng)飛輪出現(xiàn)故障以及飽和時(shí)，設(shè)計(jì)怎樣的控制方案，能使衛(wèi)星姿態(tài)系統(tǒng)仍能穩(wěn)定運(yùn)行。

2 控制器設(shè)計(jì)與穩(wěn)定性分析

首先考慮在衛(wèi)星存在不確定干擾和飛輪安裝偏差的情況下如何設(shè)計(jì)控制律u，使系統(tǒng)漸近穩(wěn)定。

如果使用偽逆法將控制力矩分配到各個(gè)飛輪，則：

(11)

式中：u∈R3為控制模塊計(jì)算得到的所需的控制力矩。將式(6)、(7)和(11)代入式(3)中可得：

(12)

設(shè)計(jì)滑模變量s=we+βe，可得：

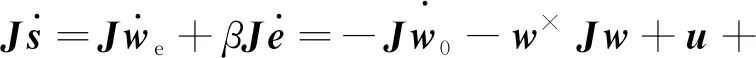
(13)

定義

(14)

則

(15)

設(shè)計(jì)Lyapunov函數(shù)

(16)

則

(17)

設(shè)計(jì)控制律

u=-A-ksgn(s)-kss

(18)

式中:k、ks為待確定的正常數(shù)。代入式(17)中：

(19)

式中:sTksgn(s)=k‖s‖，代入式(19)可得

(20)

由假設(shè)1和假設(shè)3可知

(21)

將控制律代入可得

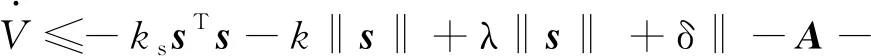
(22)

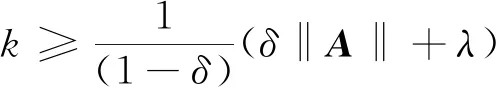
(23)

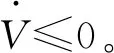
控制律中的ks和滑模矢量參數(shù)β的取值如下：

(24)

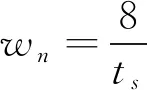
ts為要求的響應(yīng)時(shí)間，根據(jù)控制任務(wù)需求選取。值得一提的是，在滑模控制的實(shí)際應(yīng)用中，由于慣性、滯后等因素的存在，會(huì)不可避免的產(chǎn)生抖振。使用邊界層法，即用飽和函數(shù)sat(s)代替符號(hào)函數(shù)(開(kāi)關(guān)函數(shù))sgn(s)，可以達(dá)到削弱抖振的目的，并提高仿真速率。這里取飽和函數(shù)為：

(25)

并令ε=0.001。

3 動(dòng)態(tài)控制分配策略

從前面的分析可知，僅僅使用偽逆法進(jìn)行力矩分配是無(wú)法應(yīng)對(duì)飛輪故障的。所以這里使用動(dòng)態(tài)控制分配處理飛輪故障。

3.1 優(yōu)化目標(biāo)

動(dòng)態(tài)控制分配問(wèn)題本質(zhì)上是一個(gè)優(yōu)化問(wèn)題，求解它是一個(gè)數(shù)學(xué)規(guī)劃問(wèn)題。選擇l2范數(shù)作為優(yōu)化目標(biāo)：

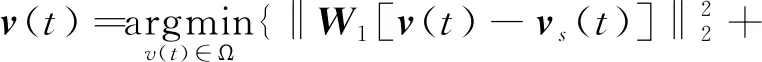
(26)

s.t.

(27)

式中:v(t)∈Rm為所求的飛輪力矩指令，vs(t)∈Rm為期望的穩(wěn)態(tài)飛輪力矩，v(t-T)∈Rm是上一時(shí)刻的飛輪力矩指令，W1和W2為對(duì)角權(quán)值矩陣；u(t)∈Rn為虛擬控制力矩，D0∈Rn×m是安裝矩陣的標(biāo)稱部分，Ω表示飛輪控制力矩的可行域。

文獻(xiàn)[11]中將W1矩陣對(duì)角線元素設(shè)置為最大限幅值倒數(shù)，但這種方法并沒(méi)有將飛輪故障的影響考慮在內(nèi)。事實(shí)上，當(dāng)星上故障檢測(cè)系統(tǒng)已經(jīng)發(fā)現(xiàn)某飛輪存在故障，則應(yīng)增大W1對(duì)應(yīng)的對(duì)角線值，使分配時(shí)盡量減少使用該飛輪。根據(jù)這兩個(gè)方面的要求，本文將文獻(xiàn)中的方法加以改進(jìn)，將W1對(duì)角線元素設(shè)置為：

(28)

3.2 求解

在不考慮飽和影響的情況下，優(yōu)化問(wèn)題變?yōu)椋?/p>

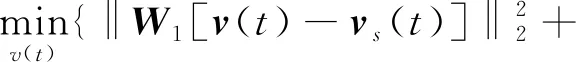
(29)

s.t.

D0v(t)=u(t)

(30)

根據(jù)文獻(xiàn)[12]，可得優(yōu)化問(wèn)題的解為：

v(t)=Evs(t)+Fv(t-T)+Gu(t)

(31)

(32)

4 零空間法

采用零空間法處理飛輪飽和。

安裝矩陣D∈Rn×m，存在一組m-n個(gè)m維正交向量，它們構(gòu)成了Rm上D的零空間的一組基。將這組向量組成的矩陣記為N∈Rm×(m-n)，即滿足DN=0，則DNx=0,?x∈Rm-n，記vm=Nx。向量vp滿足Dvp=u，則向量v=vp+vm有下式成立：

u=Dv=D(vp+vm)=Dvp+DNx+
Dvp+0·x=Dvp=u

(33)

式(33)說(shuō)明若初始解vp加上一個(gè)由D的零空間基組成的向量vm，等式仍成立。所以，基于零空間控制分配方法就應(yīng)用了這一思路：給定了初始解vp，滿足Dvp=u，在vp?Ω時(shí)，尋找x，使得v=vp+vm=vp+Nx∈Ω成立。

若經(jīng)過(guò)計(jì)算后得到的v滿足了所有分量未超出約束范圍，則將修正結(jié)果輸出到執(zhí)行機(jī)構(gòu)，若還存在超出約束范圍的分量，則重復(fù)以上的修正過(guò)程。值得注意的是，以上方法存在多次迭代仍不能使所有分量都落入約束范圍內(nèi)的情況，這時(shí)需要設(shè)定一個(gè)最大迭代次數(shù)，若仍有超出約束范圍的分量，就將其置于極限值后停止修正，這時(shí)輸出的執(zhí)行機(jī)構(gòu)命令雖然無(wú)法合成要求的控制量，但避免了多次迭代浪費(fèi)寶貴的控制時(shí)間。

5 仿真校驗(yàn)

5.1 仿真實(shí)驗(yàn)

設(shè)衛(wèi)星的轉(zhuǎn)動(dòng)慣量矩陣：

J0=diag(6.292,9.650,5.477)kg·m2

(34)

設(shè)系統(tǒng)初始姿態(tài)角為θ0=[10 10 10]o或θ0=[45 45 45]o兩種值。

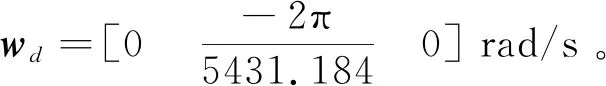
考慮4個(gè)反作用飛輪按照αi=35.25°,βi=45°(i=1,2,3,4)的標(biāo)稱安裝角安裝于衛(wèi)星上。則由文獻(xiàn)[13]可知

(35)

外干擾在三個(gè)通道上均設(shè)置為：

uf=0.0005sin(0.1t)N·m

存在安裝偏差角Δαi,Δβi。仿真中Δαi(i=1,2,3,4)在[-4.5° 4.5°]之間隨機(jī)選擇，Δβi(i=1,2,3,4)在[-5.5° 5.5°]之間隨機(jī)選擇。

仿真中的飛輪故障設(shè)置為某飛輪完全失效,其他飛輪能正常運(yùn)轉(zhuǎn)，既在仿真中對(duì)應(yīng)的飛輪效率矩陣的對(duì)角線元素為0。設(shè)置飛輪最大位置限制為±0.25N·m，轉(zhuǎn)速最大限制為0.03N·m/s。取ts=60s。設(shè)計(jì)以下3種條件：

仿真1：初始姿態(tài)角[10° 10° 10°]，未發(fā)生飽和，3號(hào)飛輪完全失效。仿真結(jié)果如圖1～2所示。

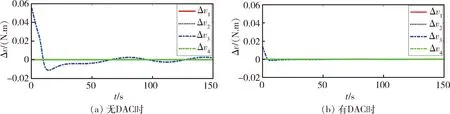
圖1 飛輪指令與實(shí)際產(chǎn)生的力矩差

仿真2：初始姿態(tài)角[45° 45° 45°]，發(fā)生了飽和，飛輪正常。仿真結(jié)果如圖3所示。

仿真3：初始姿態(tài)角[45° 45° 45°]，發(fā)生了飽和，且2號(hào)飛輪完全失效。仿真結(jié)果如圖4所示。

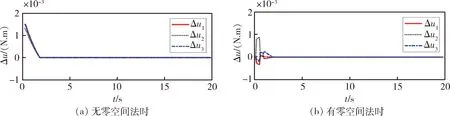
圖2 虛擬力矩與實(shí)際輸出力矩差

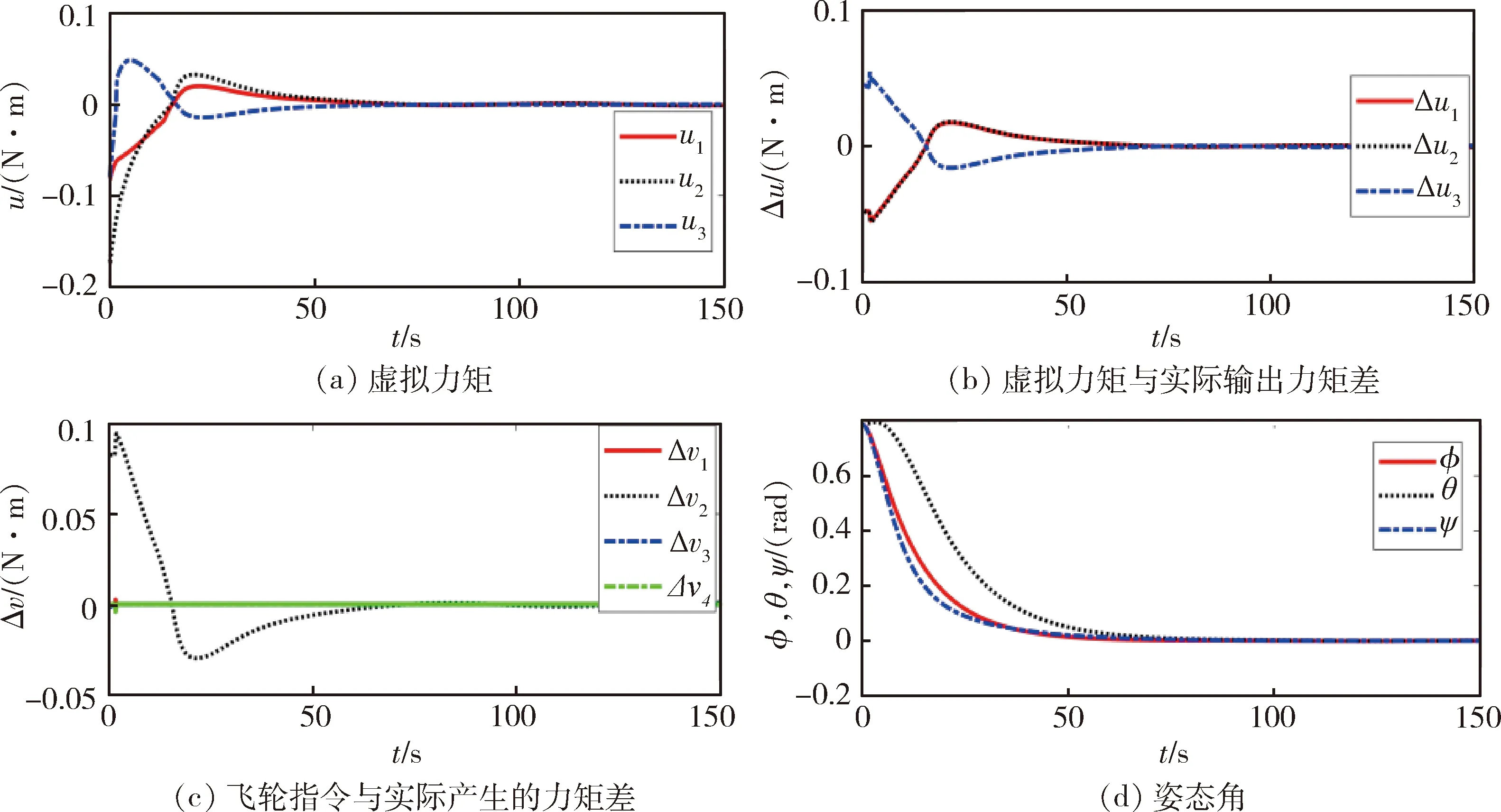
圖3 無(wú)DAC，無(wú)零空間法仿真結(jié)果

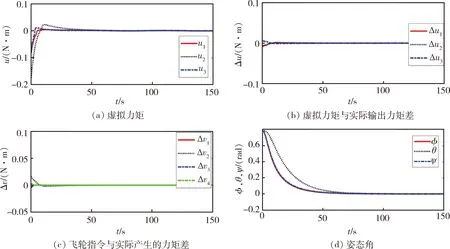
圖4 有DAC，有零空間法仿真結(jié)果

5.2 結(jié)果分析

通過(guò)對(duì)比仿真1中的兩組實(shí)驗(yàn)結(jié)果，發(fā)現(xiàn)在同樣的控制目標(biāo)下，相對(duì)于無(wú)DAC時(shí)，有DAC時(shí)飛輪更好地跟蹤了力矩指令，且穩(wěn)態(tài)不存在波動(dòng)。這是由于無(wú)DAC時(shí)，違逆法仍然將控制力矩按照安裝矩陣的偽逆分配給3號(hào)飛輪較大的力矩，但此飛輪無(wú)法響應(yīng)，導(dǎo)致其輸出和指令之間的差Δv很大，相應(yīng)的會(huì)造成較大的Δu。有DAC時(shí)，失效飛輪對(duì)應(yīng)的W1矩陣對(duì)角線元素增大，抑制了向3號(hào)飛輪分配較大的力矩，所以，使Δv減小，降低了分配誤差。

通過(guò)對(duì)比仿真2中的兩組實(shí)驗(yàn)結(jié)果，發(fā)現(xiàn)有零空間法時(shí)，Δu三個(gè)分量的絕對(duì)值都有所減低，證明了零空間法對(duì)飽和影響的抑制作用。這是由于發(fā)生飽和時(shí)，無(wú)零空間法時(shí)，超出飛輪限制的力矩會(huì)被直接置于飽和值，不做其他處理，造成合成的力矩存在誤差;有零空間法時(shí)，首先將超出限制的分量置于飽和值，再根據(jù)算法計(jì)算剩余的分量，循環(huán)一定次數(shù)，輸出調(diào)整后的值。相當(dāng)于將飽和的分量超限部分讓剩余未飽和的分量分擔(dān)，從而降低了控制誤差。

在仿真 3中，在干擾、偏差、失效、飽和共同存在時(shí)，設(shè)計(jì)的控制方法仍能有良好的穩(wěn)態(tài)性能，說(shuō)明了設(shè)計(jì)的控制律的有效性；對(duì)比圖3和圖4兩組實(shí)驗(yàn)結(jié)果，發(fā)現(xiàn)當(dāng)失效和飽和同時(shí)存在時(shí)，在DAC和零空間的共同作用下，Δv和Δu都明顯降低，使得控制過(guò)程得到了改善。所以本文設(shè)計(jì)的控制方法不僅能使系統(tǒng)最終趨于穩(wěn)定，還能改善系統(tǒng)的控制過(guò)程，有效應(yīng)對(duì)本文中的姿態(tài)控制問(wèn)題。

6 結(jié)論

研究了不確定干擾、飛輪安裝偏差、故障、飽和同時(shí)存在時(shí)的衛(wèi)星姿態(tài)控制問(wèn)題。首先針對(duì)衛(wèi)星姿態(tài)在不確定干擾和飛輪存在安裝偏差時(shí)設(shè)計(jì)滑模控制律，并驗(yàn)證了其穩(wěn)定性；而后分別應(yīng)用動(dòng)態(tài)控制分配和零空間法處理飛輪故障和飽和。最后設(shè)計(jì)對(duì)比仿真，仿真結(jié)果與預(yù)期一致，證明了設(shè)計(jì)的控制方法對(duì)本文中的姿態(tài)控制問(wèn)題的有效性。并且在降低穩(wěn)態(tài)和動(dòng)態(tài)誤差方面都取得了一定的效果。本文設(shè)計(jì)的控制方法避免了復(fù)雜的控制器設(shè)計(jì)過(guò)程，適應(yīng)性更廣，更易于工程應(yīng)用。