升力式飛行器最短返回時間離軌點設計方法

丁 寧 李兆亭 張洪波

國防科技大學空天科學學院，長沙 410073

0 引言

在載人空間飛行、天地往返運輸等空間任務結束后，需要空天飛行器返回預定著陸場，離軌制動是返回的第一步。離軌制動是指飛行器通過施加推力矢量改變原來的運行軌道，從而進入地球大氣層的軌道改變過程。離軌點設計是根據飛行器運行軌道和任務參數，確定星下點軌跡和可達域范圍，通過選擇合適的軌道位置進行離軌制動，使飛行器最終滿足再入點約束條件。

針對再入飛行器返回過程中的再入段，國內外學者進行了諸多的研究，包括再入軌跡優化方法[1-2]再入制導方法[3-4]、再入姿態控制方法[5-6]等，而對再入飛行器離軌段的軌道設計問題研究相對較少。早期研究主要將終端狀態約束設定為范圍約束，因此不同目標函數下最優解對應的大氣進入狀態存在差異[7]。后期的研究大多將約束設定為固定的再入點位置和再入參數。其中，史樹峰等[8]通過規劃離軌制動時機和離軌控制參數，實現指定再入點位置的飛行器離軌任務；龔宇蓮等[9]設計了一種航天器自主離軌制動控制算法，可根據再入點狀態約束確定離軌過渡段的平均軌道根數，實時預報再入點航跡傾角；郭付明等[10]綜合考慮優化精度和運行時間，提出了一種離軌點尋優方法，可以降低軌道機動過程中對不確定因素的敏感性。然而上述各成果研究對象多為傳統彈道式飛行器，在設計過程中往往忽略橫向機動能力對離軌點的影響。而升力式飛行器升阻比大，再入過程中橫向機動能力強[11]，當再入橫程確定時，相比于彈道式飛行器，縱程的取值范圍較大，對應再入點的位置范圍較大。基于此，綜合考慮再入點位置變化，有必要對約束條件進行設置，以優化離軌段時間，拓展離軌窗口范圍。

本文考慮升力式飛行器的橫向機動能力，提出了一種最短時間返回的離軌點設計策略。首先，根據星下點軌跡與著陸場的位置關系及各階段航程角的幾何關系，分別建立了位置約束和時間約束模型；然后根據給定的再入角和離軌能量約束，利用二體軌道理論推導了離軌點和再入點速度傾角、地心距及航程角之間的關系，并提出了一種基于牛頓迭代公式的離軌航程角尋優方法；最后計算返回段總時間，采用非線性優化方法求解最短時間返回軌道，確定離軌點。

1 最短返回時間離軌點設計流程

再入飛行器從運行軌道到達指定著陸場，依次經歷等待段、離軌制動段、過渡段、再入段和著陸段。將離軌制動與過渡段合稱離軌段。

如圖1所示，Oe為地心，O，K，E和P分別為飛行器當前位置、離軌點、再入點和著陸點，rk和re分別為離軌點和再入點地心距，Δtw，Δtk和Δte分別為等待段、離軌段和再入段時間，Δβw，Δβk和Δβe分別為等待段、離軌段和再入段航程角，Θk和Θe分別為離軌制動結束后的當地速度傾角和再入角。離軌制動段為有限推力制動，但因時間較短，可簡化，以脈沖推力代替。在此基礎上，本文設計滿足位置、時間及過程約束的離軌軌道。計算步驟可歸納為：

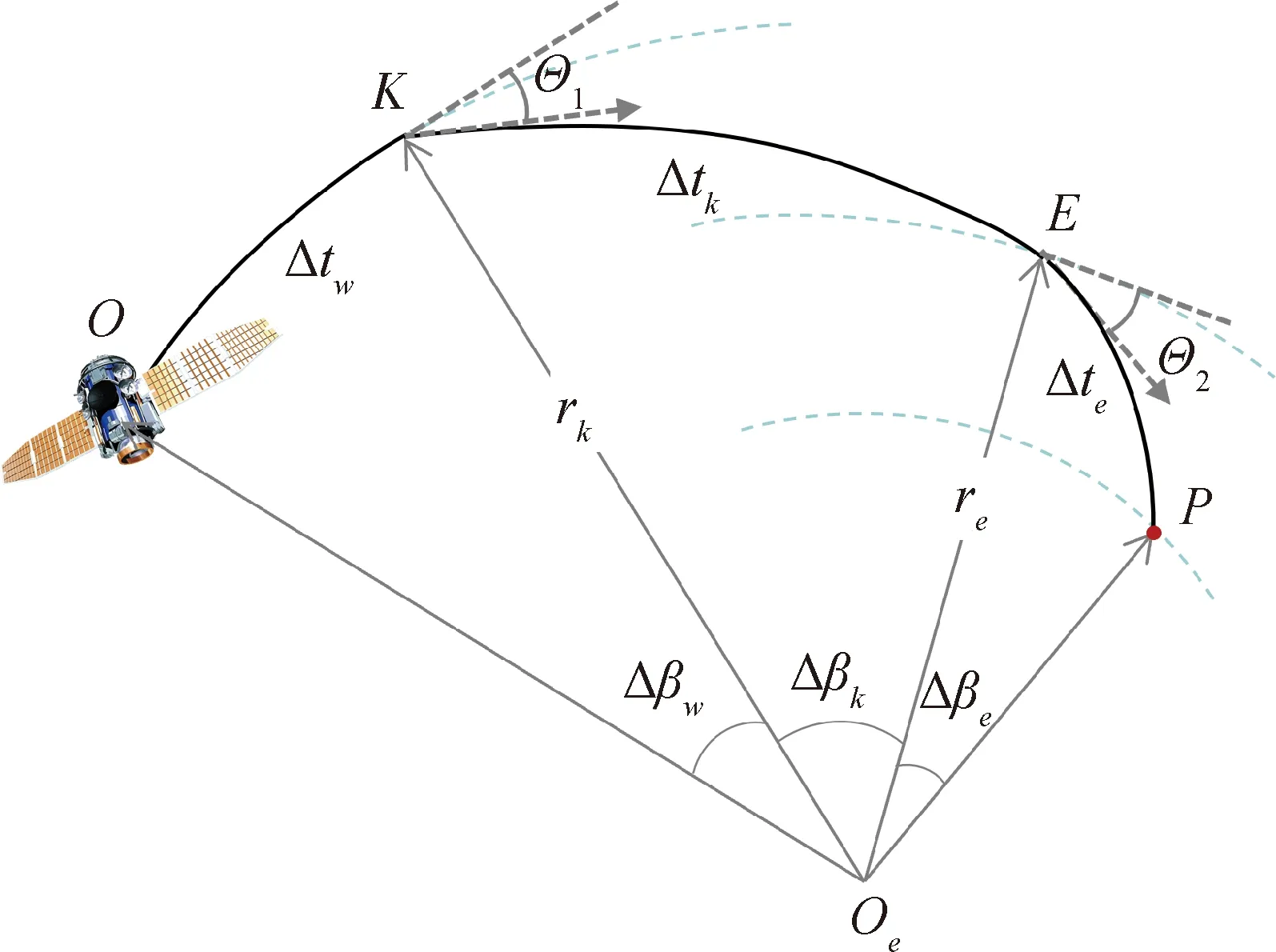
圖1 再入飛行器返回過程示意圖

1)根據飛行器當前軌道根數[a,e,i,ω,Ω,M]，確定一個周期內的星下點軌跡；

2)計算著陸點與星下點軌跡的最小橫向距離dmin、著陸點與飛行器當前位置的縱向航程角Δβ；

3)根據飛行器總體參數計算再入可達域，判斷是否滿足橫向位置約束，若滿足，則可得到不同橫、縱程對應的再入時間Δte；若不滿足，將初始時刻后推一周期重新計算；

4)由軌道根數計算得到rk，并基于給定的re，Θe和能量約束Δvmax，計算不同增益速度Δv對應的離軌時間Δtk，尋優得到最小離軌航程角Δβkmin，進而計算由當前時刻至著陸場總時間Δt；

5)對Δt尋優，得到最短時間Δtmin，計算并輸出最優離軌點軌道根數。

其計算流程圖如圖2所示，下面幾節分別敘述其計算方法。

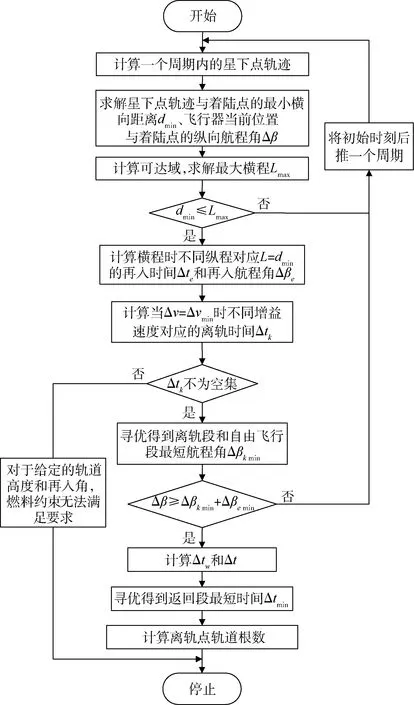
圖2 最短返回時間離軌點設計流程

2 基于再入可達域的時空約束建模與分析

2.1 再入可達域條件設計

本文以最小返回時間為離軌點設計指標，求解過程中需根據再入段時間、航程角等參數確定位置和時間約束，這些參數可由再入可達域提供。本節對再入可達域要提供的參數形式進行說明，以滿足后續設計需求。

再入可達域可描述不同縱程條件下的最大橫程，通常為橢圓形或扇形區域，常在換極坐標系中表示。如圖3所示，λpf和φpf分別為落點的經度和緯度，Z為縱程，L為橫程。

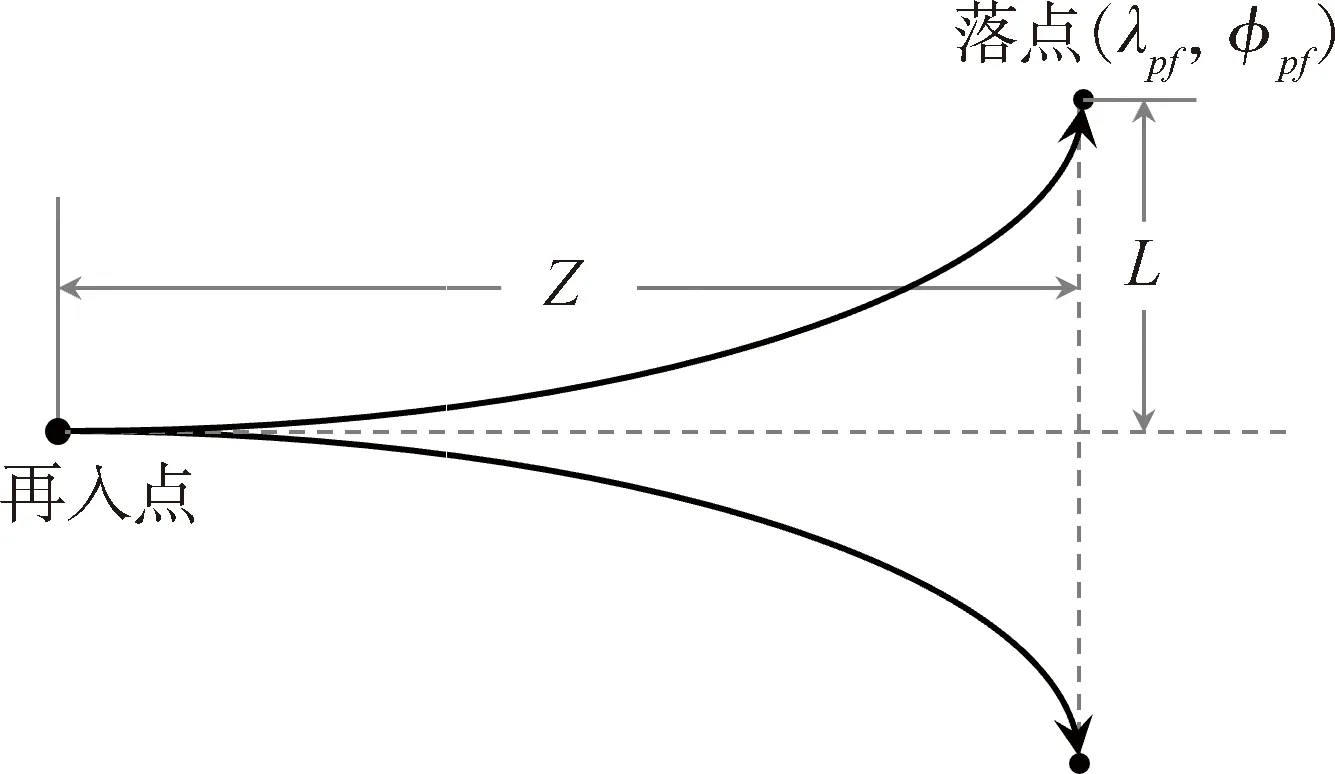
圖3 可達域示意圖

再入可達域的計算有很多經典算法[12-14]，本文不作討論。在進行離軌點設計時，首先根據飛行器總體參數和再入約束對飛行可達域進行計算，扣除再入制導預留的射程機動余量，得到最大橫程Lmax。將最大縱程等間隔劃分為m個區域，每區域橫向n等分，得到m×n個網格，如圖4所示。取網格點為樣本點，以數表的形式給出每個樣本點的再入縱程Z、橫程L及時間Δte，作為離軌點設計的輸入量給到系統中，如表1所示。

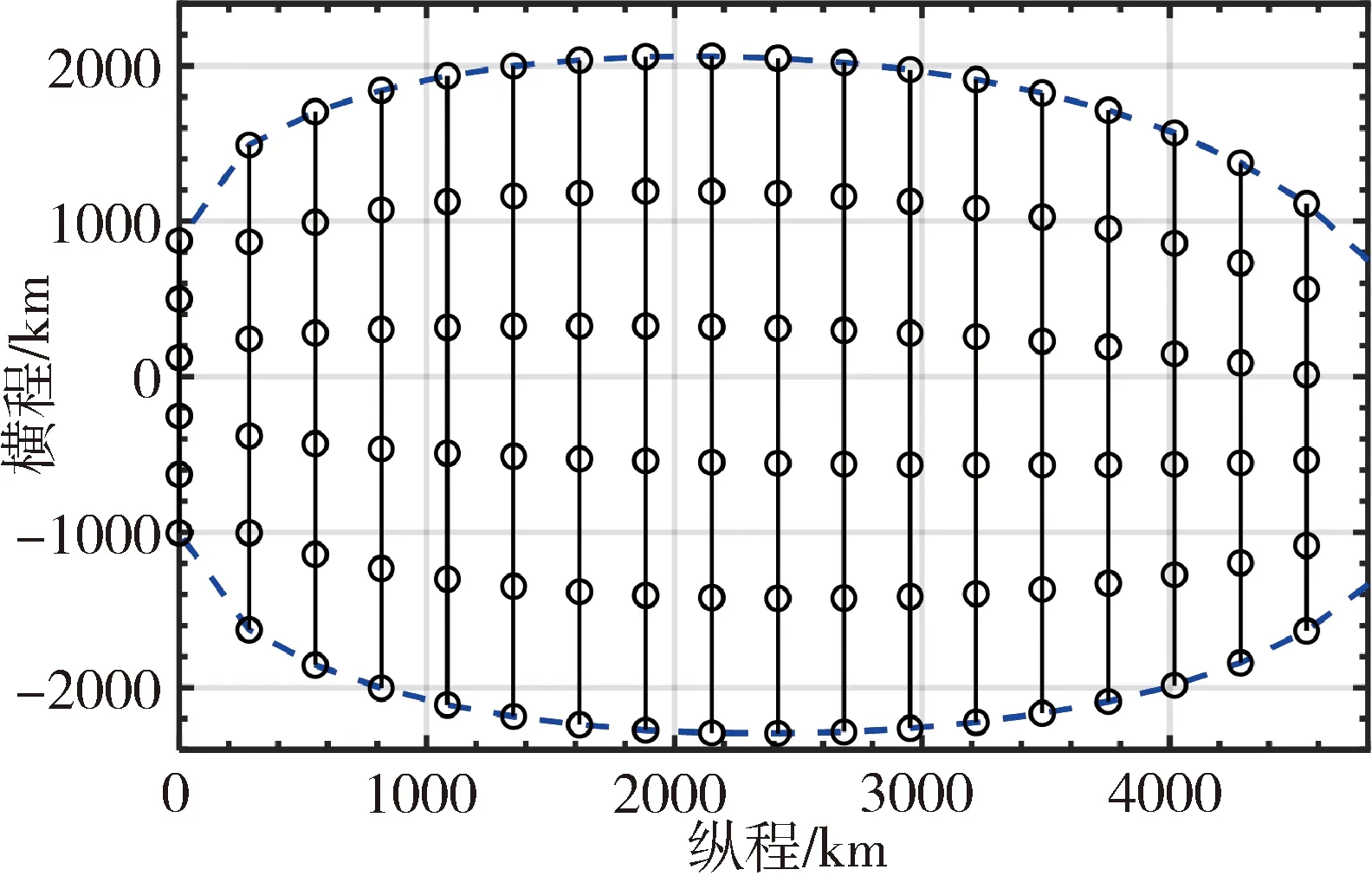
圖4 可達域網格劃分

表1 可達域輸入參數表

在輸入樣本點再入時間參數后，對于橫、縱程分別為L和Z的著陸點，可通過拉格朗日插值多項式計算再入時間擬合值

Δte(L,Z)=

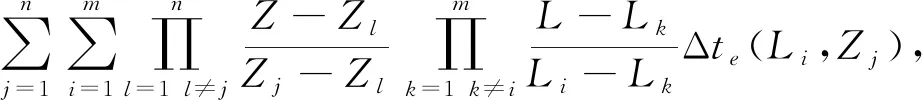
(1)

以及該落點對應的再入航程角

(2)

式中:Re為地球平均半徑。

2.2 橫向位置約束

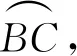
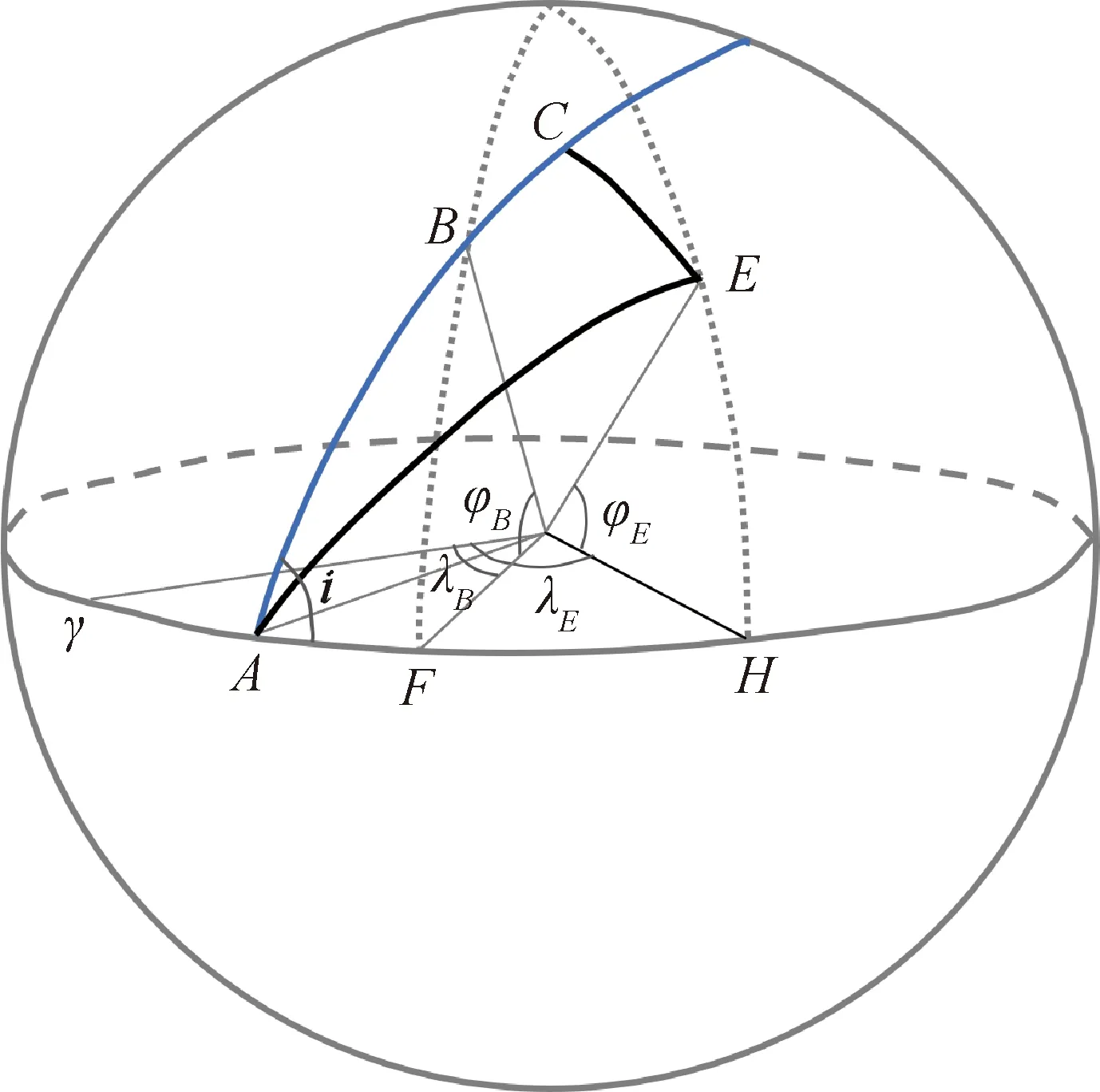
圖5 著陸點與星下點軌跡的最小橫向距離示意圖

(3)

實際上，由于地球自轉，在協議地心慣性坐標系中，E點方位角是不停變化的。按下述公式進行迭代

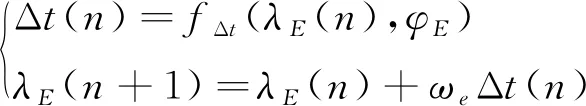
(4)

則最小橫向距離

dmin=fd(λE(n),φE)

(5)

2.3 時間約束

由于燃料有限、再入橫程確定，離軌段和再入段時間不可能無限小，因此需要考慮最短時間帶來的時間約束。以當前時刻作為起始時刻t0，設從該時刻至著陸點的飛行時間為Δt，則滿足

Δt=Δtw+Δtk+Δte

(6)

時間約束可表示為

Δtw≥0

(7)

即Δt≥Δtkmin+Δtemin。式中Δtkmin為離軌段最小時間，其計算方法將在3.2節給出，Δtemin=Δte(dmin,Zmin)為再入段最小時間，可由式求得。當Δt<Δtkmin+Δtemin時，不滿足時間約束，一個周期內無論離軌點在任何位置，飛行器都不可能到達著陸點，需在軌等待一個周期后重新進行判斷，直到滿足時間約束條件，方可進行后續計算。

3 能量約束建模及最短返回時間離軌點求解

飛行器由運行軌道進入過渡軌道、飛行到再入點，需要由制動火箭發動機提供制動速度增量。由于攜帶燃料有限，發動機所能提供的速度增量也是有限的。本節首先研究制動能量約束下滿足再入角要求的離軌點位置范圍，再綜合考慮等待段、離軌段及再入段時間，對離軌點位置進行優化求解。

3.1 LVLH坐標系下軌道方程

假設地球為均質圓球，則制動發動機關機后飛行器將沿二體軌道運行。在LVLH坐標系[17]中，將飛行器二體軌道運動方程進行投影，可得

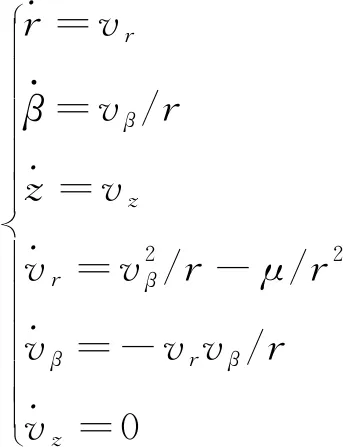
(8)

式中:z為側向位移大小，vr，vβ和vz分別為速度矢量v在r軸、β軸和z軸上的分量，μ為地球引力常數。

假設在初始時刻，航天器位于軌道上的O點，當前的運動狀態rk和vk可以由導航系統提供，再入點E的地心距re已知，則需要設計離軌軌道，使得飛行器到達再入點時，滿足再入角Θe和速度沖量Δvmax的要求。下一節將根據二體軌道邊值理論求解該問題。

3.2 基于再入角的離軌速度增量求解

軌道方程建立后，在給定再入角條件下，為快速確定能量約束下的離軌點位置范圍，需要推導離軌速度增量與離軌航程角的解析關系式。根據二體軌道理論，有

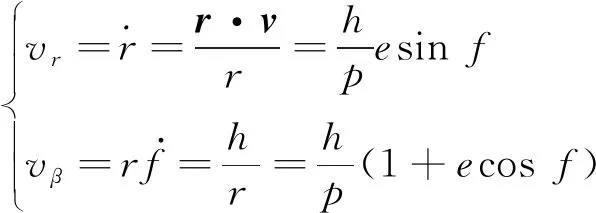
(9)

式中:f為真近點角，p為半通徑，e為偏心率。注意到Δf=Δβ，整理得

(10)

由上式可知(vrk+vre)和(vβk-vβe)成比例。故有

(11)

將式(11)代入式(10)，得到Θk與Θe的關系式

(12)

根據上式，就可以由rk，r，Θe和Δβk確定出在當前點處的期望速度傾角

(13)

進而確定期望離軌軌道的半通徑及動量矩

(14)

(15)

式中:c為弦長，pm為最小能量橢圓的半通徑。進而可得到當前時刻的增益速度和轉移軌道的半長軸

Δv=vR-vk

(16)

(17)

式中:vR為當前位置的需要速度，其徑向和周向分量分別為

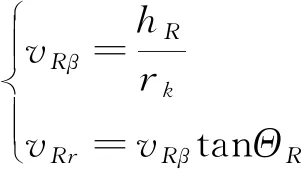
(18)

當轉移軌道是橢圓時，轉移時間可由Lagrange方程

(19)

求得，其中，α和β表示Lagrange參數，滿足

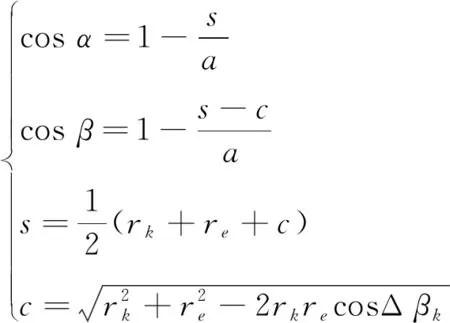
(20)

此外，當位置向量和速度向量均求得之后，離軌點和再入點的所有6個軌道要素均可以得到，故也可由開普勒方程求得轉移時間。

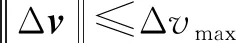
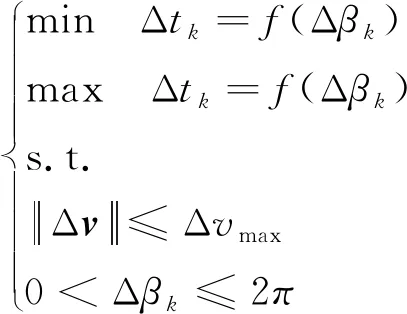
(21)

依據上述解析關系式，可以求得能量約束下離軌航程角及離軌時間的取值范圍。應用序列二次規劃算法(SQP)、信賴域反射算法等都可以實現對該問題的求解，此處不做贅述。此外，可采用牛頓迭代公式

(22)

求解最短時間。為提高計算速度，f′(Δβk)可用Richardson外推法近似得到。設誤差階數為n，外推次數為m，則根據外推公式

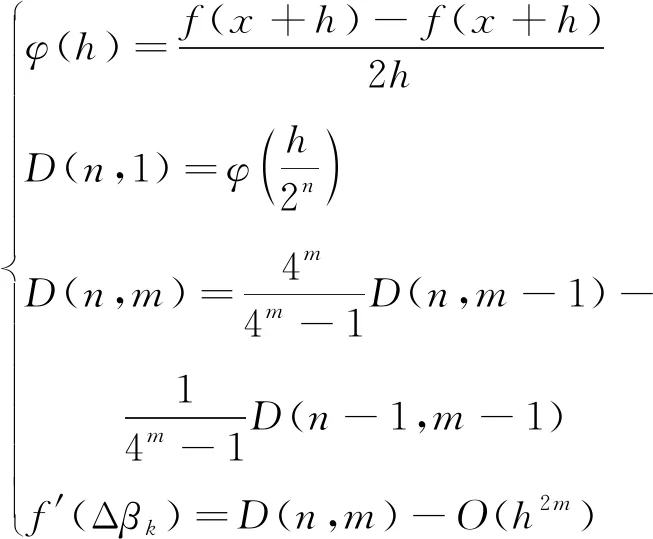
(23)

可知，當n和m足夠大時，D(n,m)可充分接近f′(Δβk)。通過求解，得到離軌航程角范圍Δβk∈[Δβkmin,Δβkmax]。

3.3 最短返回時間離軌點設計

在得到了滿足橫向位置約束、時間約束和能量約束的航程角范圍后，可將飛行器等待段航程角表示為：

(24)

式中:

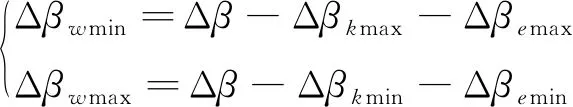
(25)

根據等待段航程角及初始軌道根數，可求得離軌點軌道根數，得到離軌窗口。以返回段離軌時間為設計指標，采用非線性優化方法對離軌點位置進行尋優，即可得到最短時間離軌點。

4 仿真校驗

本節將通過數值仿真驗證所提算法的有效性。設初始時刻t0為2022年3月29日9:00:00，飛行器位于近地圓軌道上，仿真參數見表2。

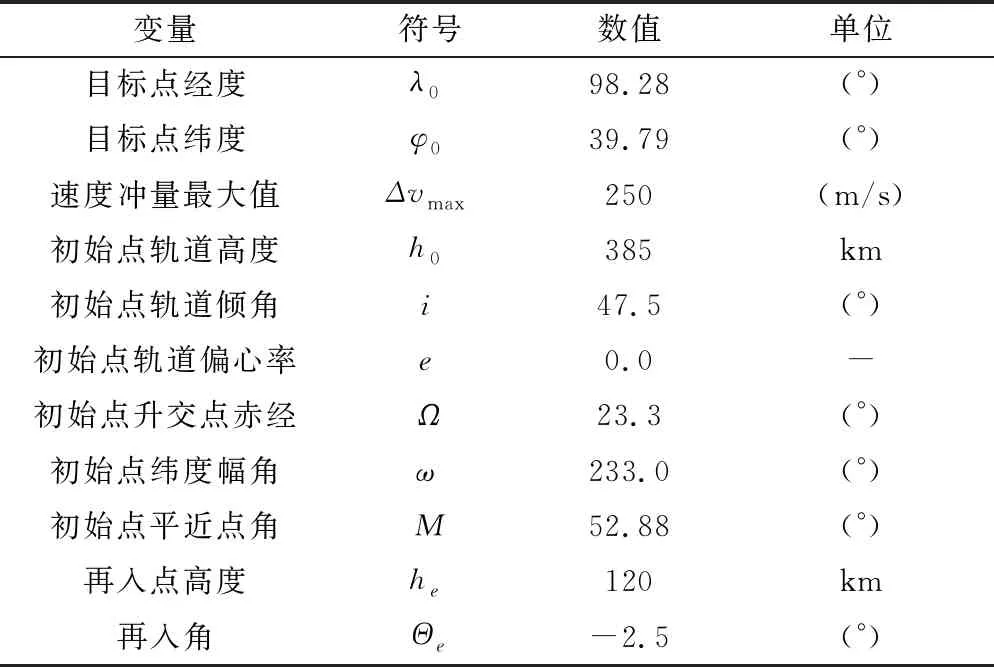
表2 仿真參數

參照升力體飛行器的性能指標，給定再入段可達域。圖6給出了可達域的實際經緯度范圍，由于考慮了地球自轉，可達域不是南北對稱的，最大橫程Lmax=2036.4km。將可達域縱程平均設置18個節點，橫程平均設置6個節點，每個節點處的再入段最小時間如表3所示。

圖6 仿真條件下可達域范圍

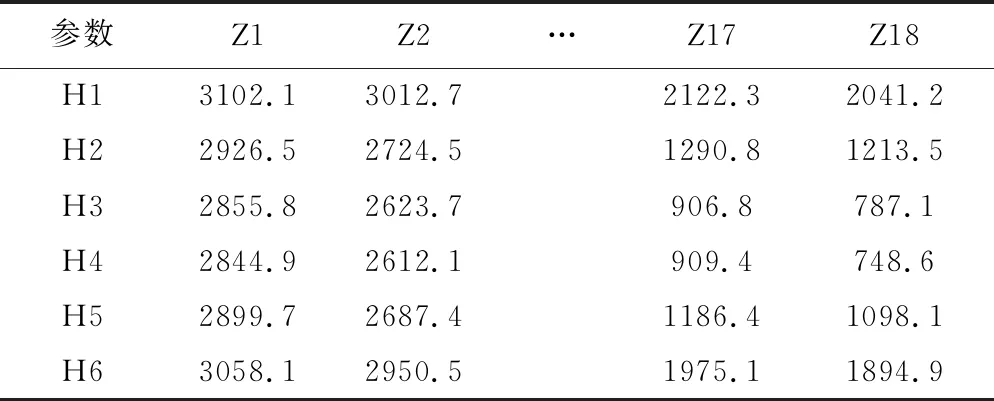
表3 各節點最小再入時間(單位：s)

根據假設，計算得到飛行器當前點至著陸點的航程角Δβ=1.92rad。利用式(5)可求得目標距星下點軌跡的最小橫向距離dmin=556.51km。由于dmin≤Lmax，故滿足位置約束。

由仿真條件，確定再入段時間取值范圍。當橫程相同時，隨著縱程的增加，再入時間增加。當橫程L=dmin時，計算得縱程取值范圍Rz∈[1083.2,4819.1]km。通過插值計算得到不同縱程對應的再入時間和再入航程角，其中最小和最大再入時間分別為Δtemin=810.17s、Δtemax=3098.60s，對應再入航程角Δβemin=0.17rad、Δβemax=0.7556rad。

下面計算離軌時間取值范圍。根據式，由離軌點及再入點高度、再入角計算得到不同離軌航程角Δβk對應的離軌時間Δtk。圖7給出了二者的關系圖，可以看出二者呈正相關，標注的紅色點表示速度沖量Δvr=Δvmax時航程角和離軌時間大小，當曲線上點在該點下方時，滿足能量約束。設離軌航程角求解精度為10-6rad，選取滿足約束的點進行迭代，分別計算離軌段最短飛行時間Δtk，迭代結果如圖8所示。

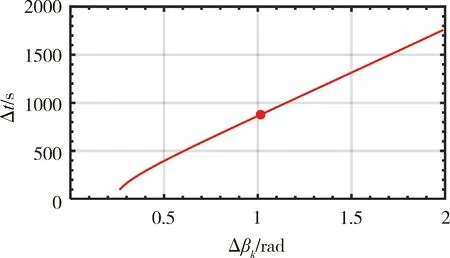
圖7 離軌航程角與離軌時間關系圖

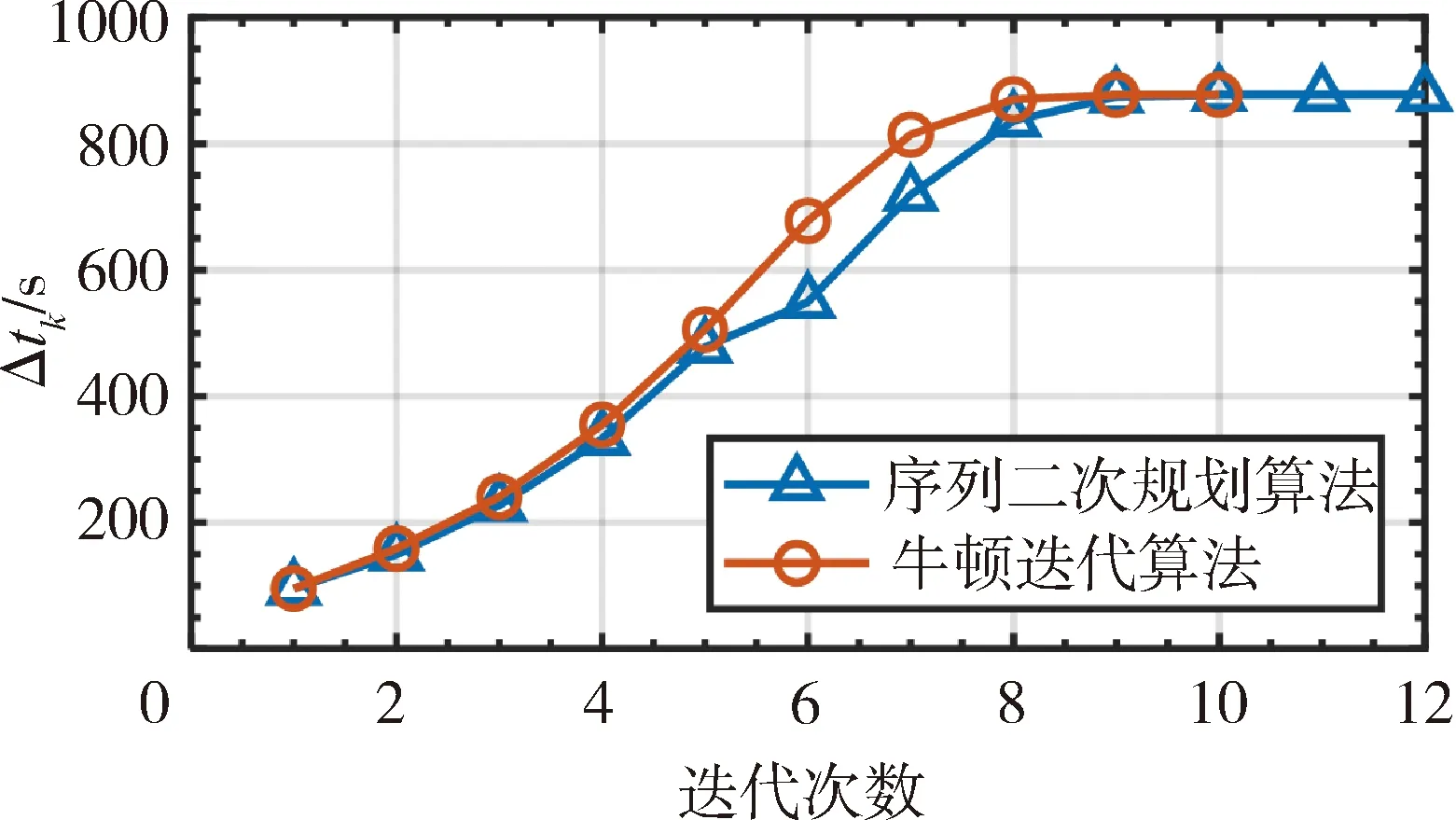
圖8 離軌段最短飛行時間迭代結果

可以看出，在合適初值條件下，兩種方法均求得Δtkmin=877.26s，對應Δβkmin=1.02rad，結果較為準確，過程較為平滑。但SQP算法迭代12次，用時0.705965s，而牛頓迭代法迭代9次，用時0.099555s，相比于SQP算法，牛頓迭代法迭代次數少、求解時間快，可以更好地實現最短離軌時間的求解。類似地，求得離軌段最大飛行時間Δtkmax=2069.9s，對應的航程角Δβkmax=2.3284rad。

在求得離軌段及再入段航程角范圍后，可進一步求得等待段航程角Δβw∈[0,0.73]rad，進而確定離軌窗口。如圖9所示，標注段表示離軌窗口。

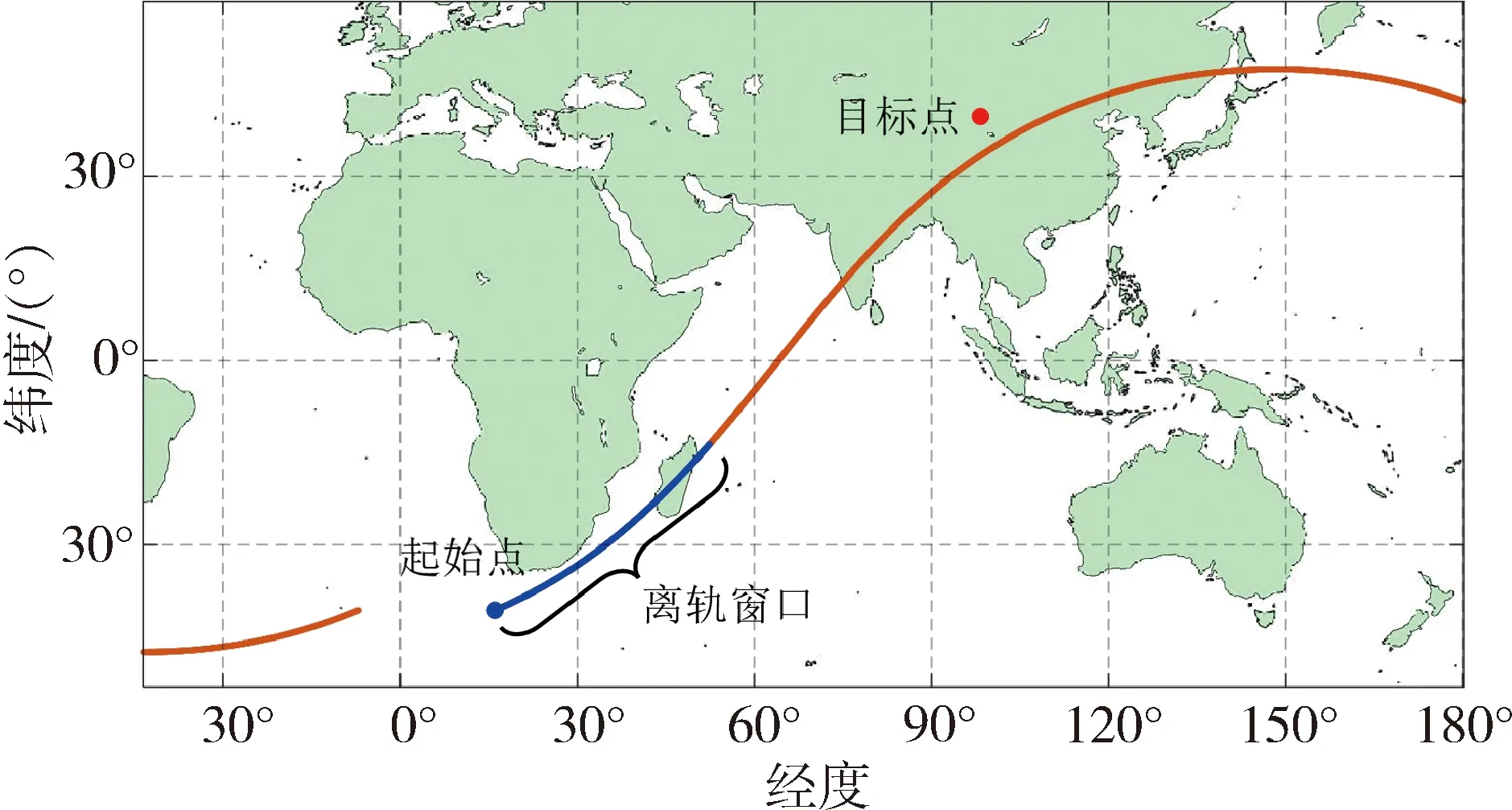
圖9 離軌窗口

由式(6)和(25)計算出不同離軌和再入航程角下的等待時間及返回總時間，在所求離軌窗口的基礎上，應用非線性優化設計方法fmincon對返回總時間進行尋優，結果如圖10所示，其中圖線①、②、③、④分別表示Δtw、Δtk、Δte和Δt的迭代過程。可以看出，在本例中，當離軌段和再入段時間均取最小值時，返回段總時間最短，為2379.2s，離軌點軌道根數如表4所示。

表4 最短返回時間離軌點軌道根數

為進一步驗證算法的適用性，分別改變飛行器初始時刻位置和著陸點位置進行仿真。飛行器初始時刻位置改變，離軌窗口也相應改變。圖11為一個回歸周期內飛行器滿足約束的離軌點集合，其中標粗部分為各圈離軌窗口。可以看出，在升力式飛行器強橫向機動優勢下，離軌窗口范圍較大，機動性和靈活性較強。

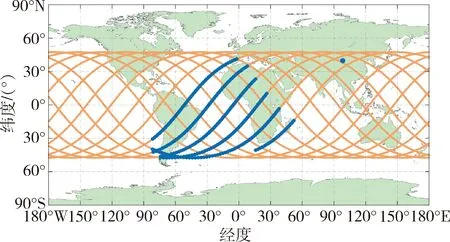
圖11 一個回歸周期內飛行器離軌窗口

當飛行器需應急返回時，往往需要改變著陸點位置。假設除了主著陸場1外，還有7個副著陸場，表5給出了各著陸場位置及最短離軌時間仿真結果。可以看出，對于不同的著陸點位置，本文所提算法均有較好的適應性。仿真結果表明，飛行器在8個著陸場均可正常著陸，其中著陸場7返回段飛行時間最短，因此可優先選擇該著陸場進行應急著陸。

表5 各著陸場位置及仿真結果

5 結論

為了實現升力式飛行器離軌點的快速設計，本文充分考慮其橫向機動能力強的特性，建立了基于再入可達域的時空約束模型，推導了燃耗約束下的離軌航程角解析計算方法，給出了確定最優制動點位置的迭代算法。通過仿真分析可以得到以下結論：

1) 多約束下的最短時間離軌點確定策略能夠滿足升力式飛行器的離軌要求。經過較少次數迭代后，離軌段航程角誤差收斂至較高精度,速度較快，結果較為準確；

2) 對飛行器不同飛行時刻的離軌窗口求解表明，本算法對于不同起始位置均有較好的適應性，升力式飛行器的橫向機動能力拓寬了其離軌窗口，增加了返回的機動性和靈活性；

3) 對不同位置著陸點的最優離軌點求解表明，當飛行器需要應急返回時，該算法能夠基于當前時刻狀態進行快速計算，通過對比確定最優著陸點，具有較強的可行性和實時性。