采用二次修正的立方星攔截仿真研究

林思穎 康國華 魏建宇 田士瑛

1.南京航空航天大學航天學院，南京 211106 2.上海衛星工程研究所，上海 201100

0 引言

隨著空間態勢競爭不斷加劇，空間攔截成為有效拒止對方空間力量的重要手段。天基動能攔截技術最早在上世紀八十年代提出，具有比陸基和海基更大的可攔截范圍。它通過航天器載體飛行至目標航天器一定距離后，發射攜帶的動能攔截器，利用其高速飛行所具有的巨大動能，通過直接碰撞的方式摧毀目標[1-2]。立方星以其成本低、周期短、便于攜帶等特點逐漸成為當今空間技術的重點發展方向，現已投入多項應用[3-5]。偵察能力和脫軌技術[6]的發展使立方星成為動能攔截器的新方案。然而，受限于立方星的自身重量，燃料消耗成為攔截過程的首要約束。

天基攔截過程通常分為3個階段：變軌導引段、慣性飛行段、精確末制導段[7]。一般基于Lambert問題的求解來設計初始軌道，即給定初末位置和轉移時間來確定軌道，最后再進行軌道優化。Lambert問題多采用數值迭代的方法對非線性的軌道動力學方程進行求解，目前已形成多種解法[8-11]。其中Bate[12]基于Gauss方程，定義普適變量χ和z，通過計算拉格朗日常數以及它們的導數求解Lambert問題。該方法適用于任意類型的軌道，解決了軌道類型確定問題。

由于各種攝動對軌道存在影響，因此即使規劃了軌道，通常也要進行修正。其中經典方法是通過不斷迭代來修正初始速度，使得末端位置滿足精度要求；也可通過修正末端位置來彌補偏差。哈爾濱工業大學張錦繡等[13]提出了修正目標位置的方法來補償Lambert問題的J2攝動誤差，但存在迭代次數過多而錯過攔截時間的問題；周敬等[14]將變化幅度較小的地心距及軌道傾角平均化為常量，使得考慮J2攝動的相對運動模型可解，但其常微分方程式較復雜，且未考慮燃料因素。北京航空航天大學周勇等[15]，提出了末端再次求解Lambert問題來減小航天器的末端脫靶量，該方法計算量小，可滿足快速性要求，同樣忽略了燃料受限問題。

綜上，由于立方星功耗、燃料和能力受限，如僅通過求解Lambert問題進行規劃，將面臨末端精度不高或燃料消耗過多等問題。鑒于末端攔截的本質是近距離下的軌道交會問題，因此本文在Lambert問題求解基礎上，在末端通過C-W方程進行導引，施加二次脈沖，對攔截軌道末端進行誤差修正。

1 問題描述

相比于傳統大衛星，立方星雖有成本低、部署靈活的巨大優勢，但同時存在體積小、攜帶燃料有限的局限性。若以立方星為攔截器，其攔截過程主要存在以下問題：

1)由于立方星攜帶燃料能力及推力器比沖限制，無法攔截空間任意點，即存在可攔截范圍；

2)空間攝動不可避免使得規劃的軌道產生偏移，無法到達理想攔截點，需修正末端脫靶量。

鑒于燃料的重要性，如何在燃料-時間約束下設計出攔截軌道成為本文的關鍵問題。為簡化問題模型又不失一般性，對攔截環境做如下假設：

1)鑒于立方星體積較小，且飛行時間短，故僅考慮J2項攝動；

2)目標航天器在軌慣性飛行，不考慮變軌；

3)立方星機動能力有限，其相對目標航天器的距離遠小于目標軌道半徑。

在以上假設條件下，立方星攔截過程如圖1所示，在地心慣性坐標系下，S點為立方星的初始變軌點，T點是立方星的攔截點，在目標航天器所處軌道上。因此本文立方星的攔截問題，就是如何設計一條滿足時間和燃料約束的軌道，使得立方星從S點出發，經歷時間Δt后在T點實現目標攔截。

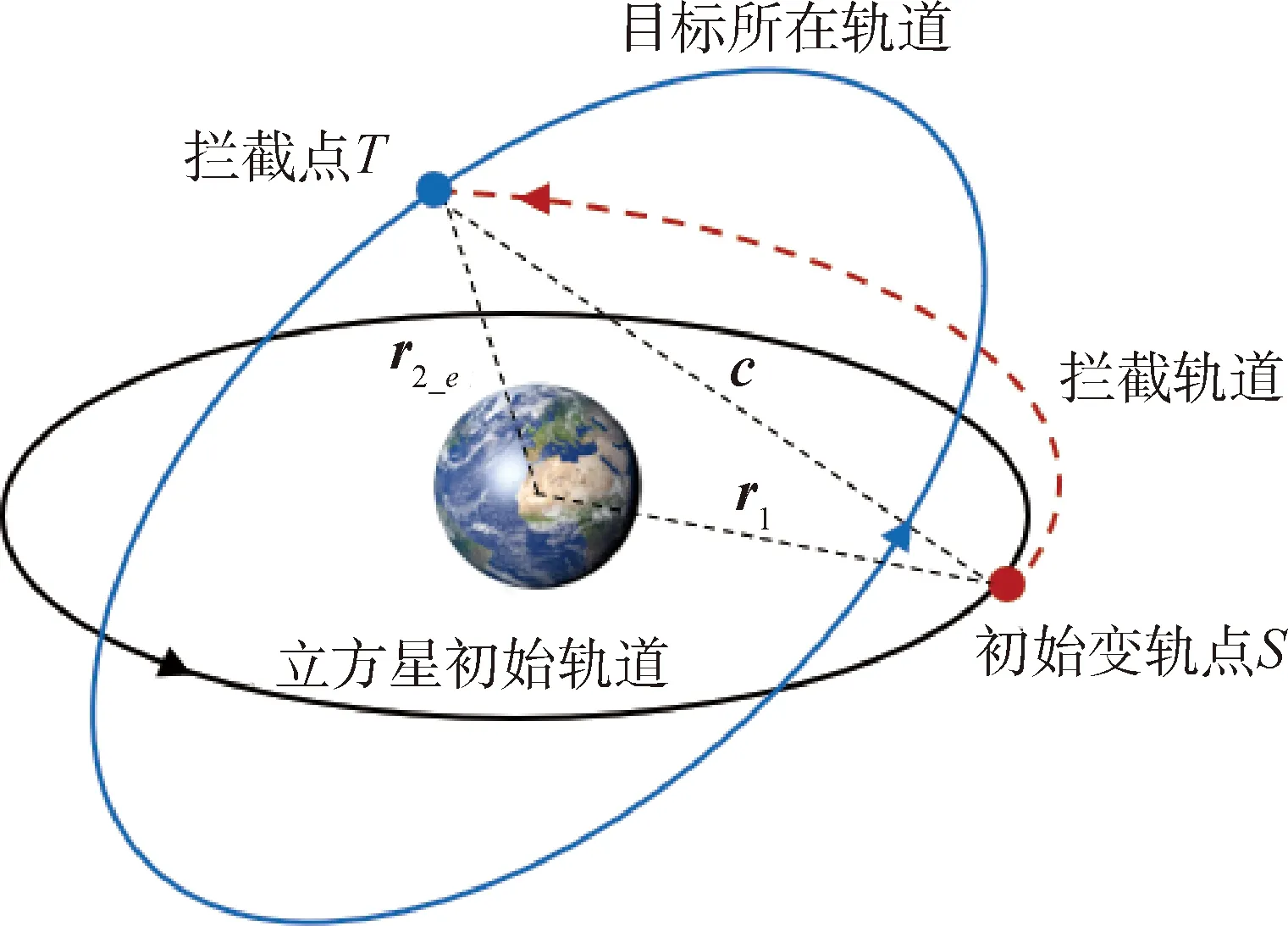
圖1 立方星攔截軌道示意圖

2 時間-燃料約束下的攔截軌道設計

由Lambert問題可知立方星從點S到點T的轉移時間Δt只取決于攔截軌道的半長軸a，距離引力中心的矢徑模之和以及兩點間弦長c[16]，即：

Δt=F(a,r1+r2_e,c)

(1)

獲得目標航天器的初始軌道根數后，通過對下式(2)的積分可獲取任意時刻目標的位置信息。

(2)

對于Lambert問題，學者們已經提出了多種解法，如Gauss算法、Battin算法、真近點角迭代算法和飛行方向角迭代算法等。本文采用普適變量法，避免分類討論軌道類型。

假設已知轉移時間Δt，通過牛頓迭代法解出z，得到拉格朗日系數f、g的表達式，進而攔截過程的始末速度可被拉格朗日函數表示為[17]：

(3)

(4)

對于攔截問題來說，通常要求在給定時間和燃料范圍內，找到使燃料消耗最小的攔截時間Δt。根據齊奧爾科夫斯基方程[18]，速度增量越大，消耗燃料質量越多，即需找到使速度增量最小的Δt。將該問題分為2層，內層求解Lambert問題，外層進行Δt的循環及速度判斷。得到一個Δt的集合，其中最小速度增量對應的攔截時間為所求解。

當力作用在立方星上的時間相比于立方星的運動時間足夠短時，可將作用力看作原地、瞬時使速度變化的脈沖。該次脈沖所產生的速度增量可表示為：

Δv1=v1_2-v1

(5)

在考慮攝動的條件下，初始脈沖仍以式(5)為準。慣性飛行后，由于J2攝動影響，攔截軌道逐漸偏離預設軌道。本文將采取C-W方程進行末段軌道修正，施加第二次脈沖來補償J2攝動引起的位置誤差。

3 基于C-W方程的末段攔截修正

攔截末段兩航天器相對距離較小，滿足C-W方程要求[19]。攔截場景如圖2所示，在目標航天器上建立相對坐標系o-xyz：以目標航天器質心o為原點，x軸為地心-目標矢量方向，z軸與目標軌道面垂直，y軸與x、z軸構成右手系。立方星相對于目標星的位置矢量為δr。

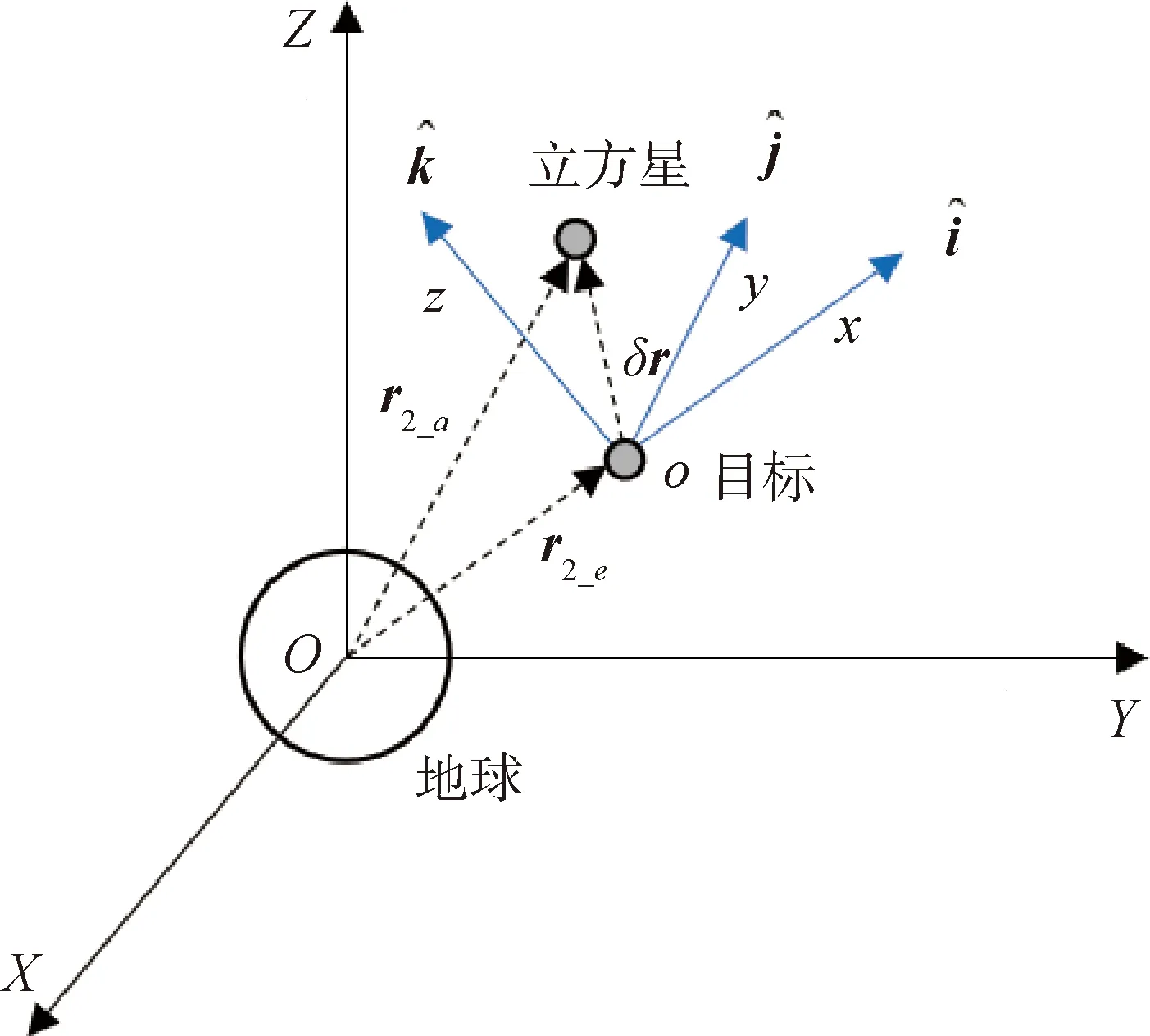
圖2 末端攔截坐標系

兩航天器的相對運動滿足：

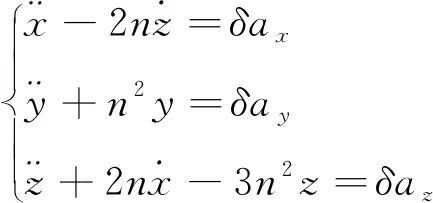
(6)

式中：x、y和z為立方星相對與目標航天器的位置，n為立方星的平均軌道角速度。

由前面假設條件已知目標航天器在軌無動力飛行，即各軸加速度為0，式(6)的解析解矩陣式[20]為：

(7)

式中：

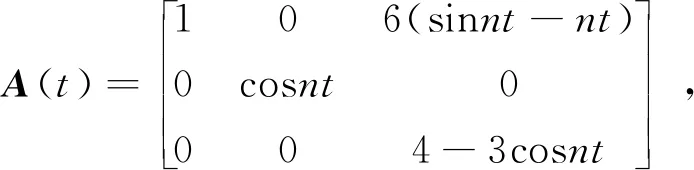
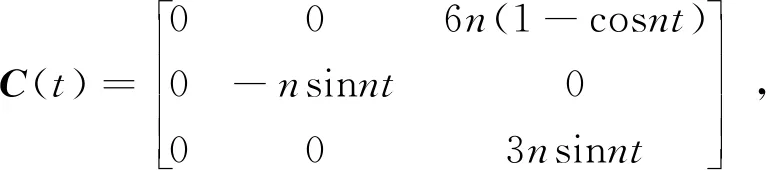
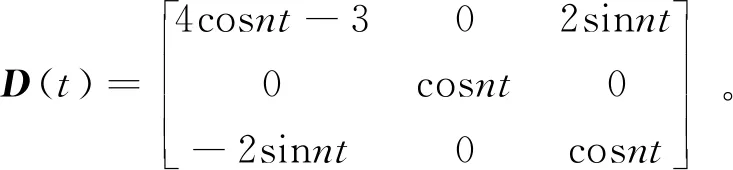
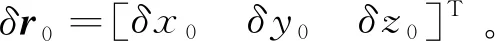
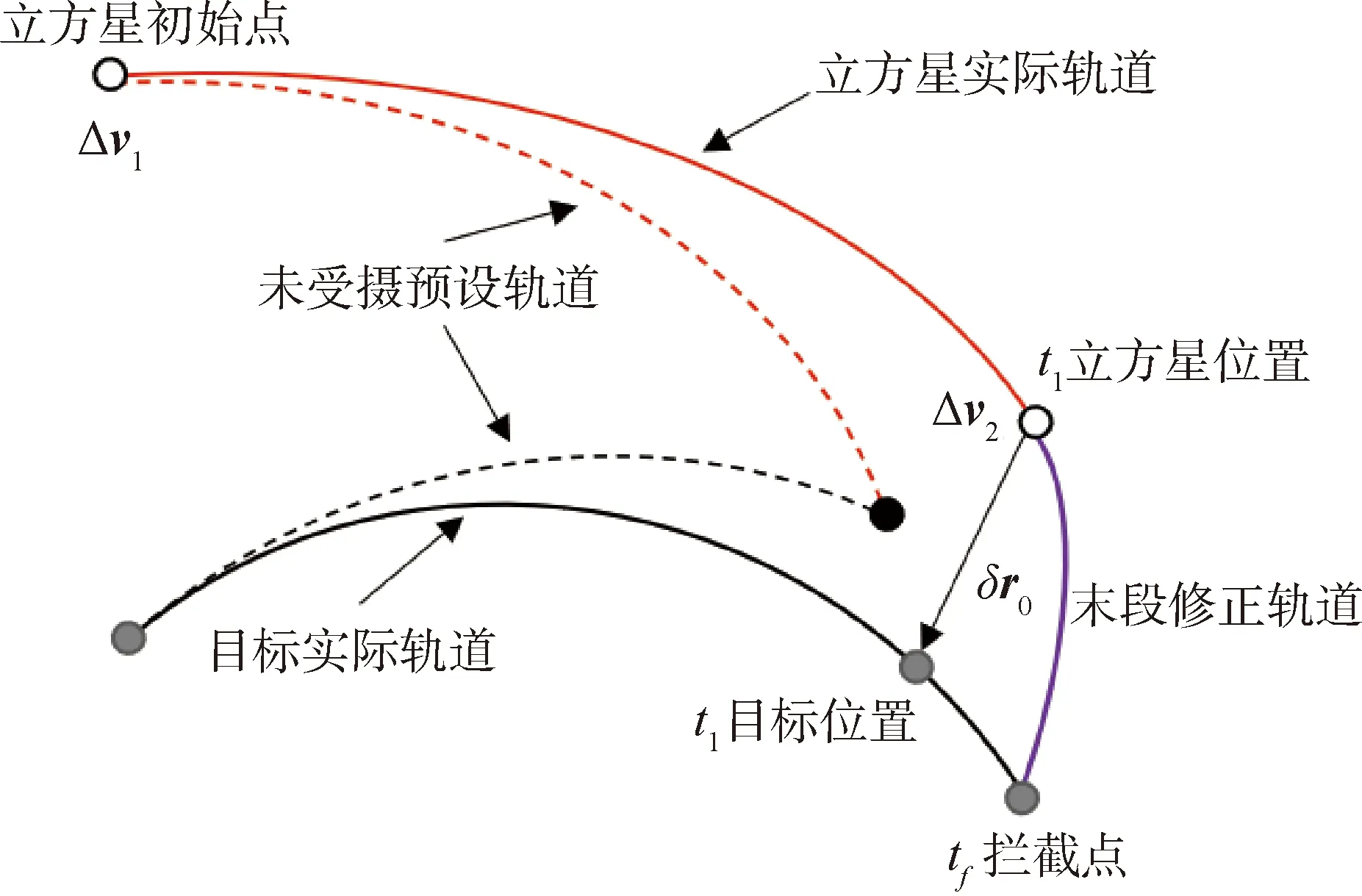
圖3 基于C-W方程的末端修正

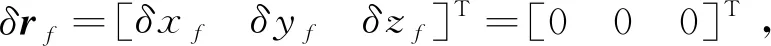
(8)

式中：G1=-B-1A,G2=B-1。

當第二次脈沖前后的相對速度已知，控制脈沖為:

Δv2=δv+(t1)-δv-(t1)

(9)

結合前面討論，二次修正下的立方星攔截軌道設計流程如圖4所示：

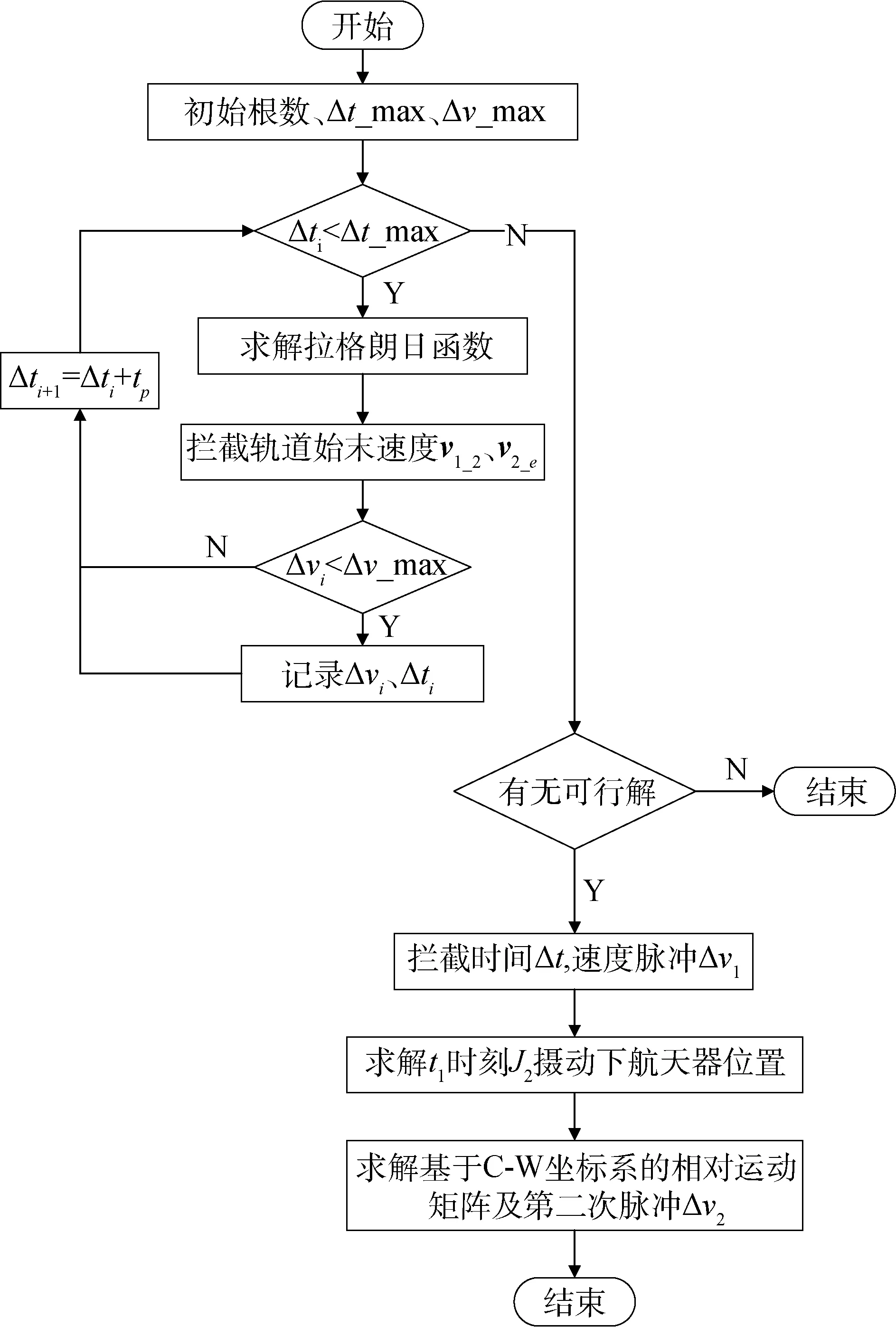
圖4 考慮攝動的立方星攔截軌道設計流程圖

根據圖4所示，兩次脈沖修正的攔截軌道設計驟如下：

1)求解二體Lambert問題，得到立方星在無攝條件下首次變軌時刻t0的速度v1_2;

2)已知t0時刻立方星的r1、v1_2及目標的r2、v2。在J2模型下，數值積分得到Δt1后立方星及目標的位置矢量;

3)已知任務時間Δt2，通過解相對運動矩陣，得到在t1時刻施加的速度脈沖Δv2。以t1時刻為起點更新軌道，得到修正軌道;

4)輸出完整攔截軌道。

4 仿真校驗

4.1 仿真參數設置

為了讓仿真更加接近真實場景，本文通過GMAT構建了仿真環境。GMAT是一個由NASA開發的開源軟件，內置了各種軌道計算模型，可以實現軌道的精確仿真；同時具有強大的三維動畫功能，能夠直觀再現航天器運動過程。本文通過Matlab驅動GMAT給出立方星和目標的軌道計算迭代，仿真過程如圖5所示。

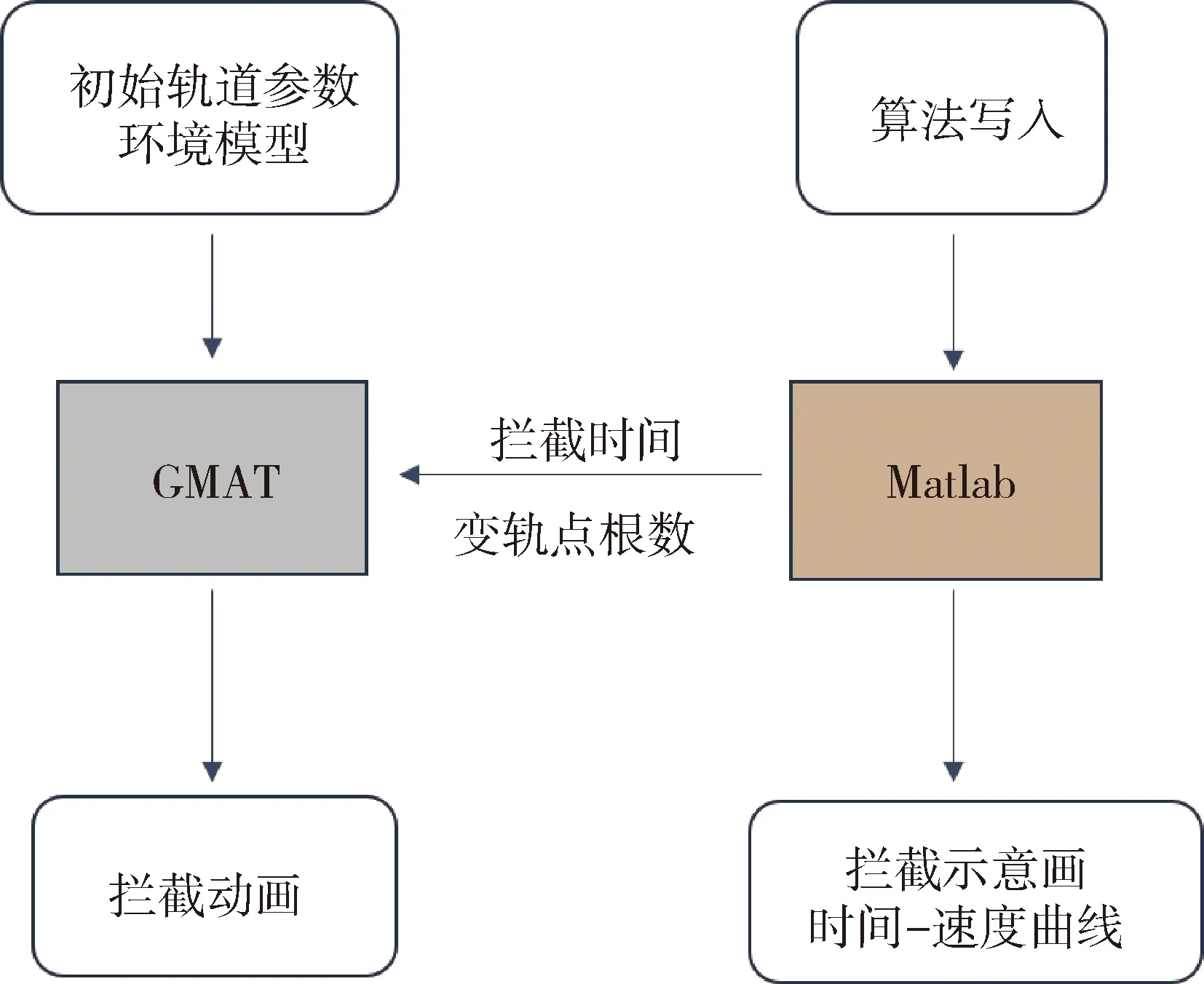
圖5 GMAT與Matlab互聯仿真框圖

聯合仿真步驟如下：

1)在Matlab中初始化立方星和目標航天器軌道、任務時間等參數；然后將Matlab與GMAT互聯，設置GMAT的仿真環境。

2)在Matlab中，根據Lambert算法求得第一次脈沖后的立方星軌道根數，將其作為GMAT中的初始根數。

3)GMAT在Matlab驅動下，輸出攔截過程的實時位置速度數據。將輸出數據中t1時刻兩航天器的狀態向量導入到Matlab中，求解二次脈沖。

4)在GMAT中配置推力器模型以實現補償脈沖，并繪制出攔截過程的動畫及對應過程的軌道信息。

鑒于立方星推進能力限制，本文設置了共軌面攔截場景，給定最長任務時間Δtmax=1800s，仿真參數如表1所示。

表1 仿真參數設置

由齊奧爾科夫斯基火箭方程，得到最大速度增量Δvmax與燃料消耗Δm間的關系如式(10)所示：

(10)

由表1比沖除總沖得到推進劑質量為80.449kg，燃質比略小于30%，符合實際。若將其全部耗盡，求得最大速度增量Δvmax=122m/s。

立方星與目標在慣性坐標系下的初始軌道根數如表2，兩者相距30km。

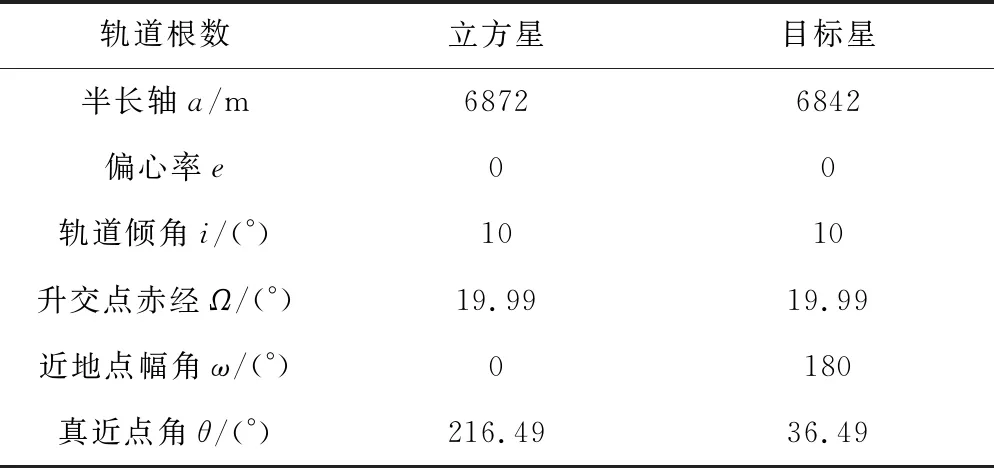
表2 兩航天器初始軌道根數

在GMAT中完成對模型的配置，在預報模型中選擇引力場模型JGM-2，數值積分方法為RungeKutta89。

4.2 仿真與分析

在表2立方星初始條件及Δvmax的約束下，考慮最長攔截時間Δtmax，通過改變目標星初始軌道的半長軸a及真近點角θ，由Lambert問題的可行解集合獲得立方星攔截的空間范圍。仿真結果如圖6所示，其中藍色區域為攔截域，即能夠被立方星攔截的目標星在初始時刻的位置集合。從圖中可以看出，上下方區域大致呈中心對稱圖形。向下攔截時兩航天器最遠相距534.36km，此時目標星的軌道高度為246km；向下攔截時最遠相距538.17km，此時目標星的軌道高度為700km。

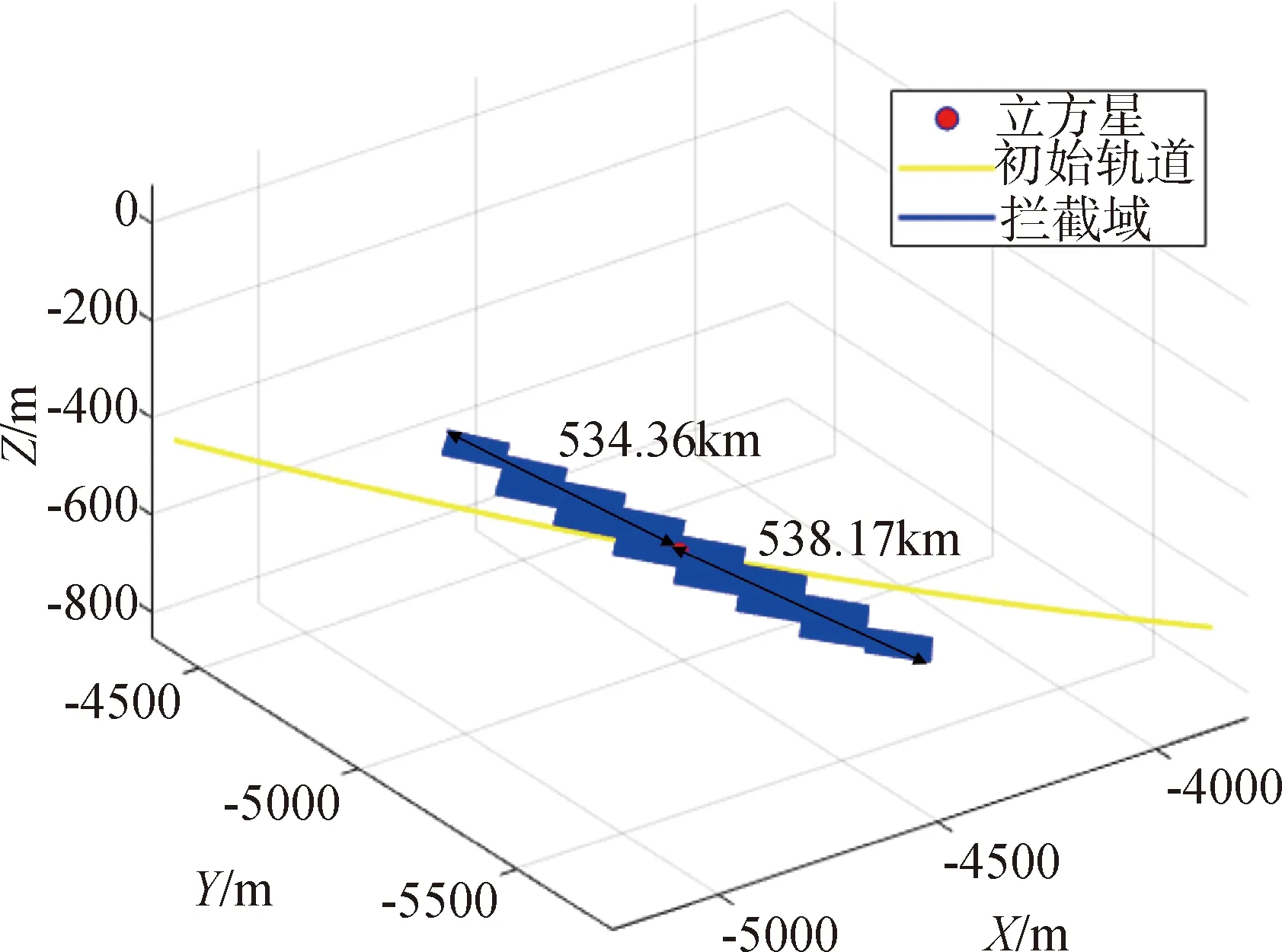
圖6 燃料約束下立方星攔截域

將表2的根數轉換為狀態量后代入式(3)，當Δt∈[0,1800]時，式(5)得到的速度增量Δv與攔截時間Δt的關系如圖7。從圖7可以看到，在最大速度增量的約束下，立方星在267s至1800s范圍內可實現攔截，即給出立方星攔截的時間范圍。在該范圍內，所需Δv隨著Δt的增長呈下降趨勢，其中Δt=1800s時Δv最小。

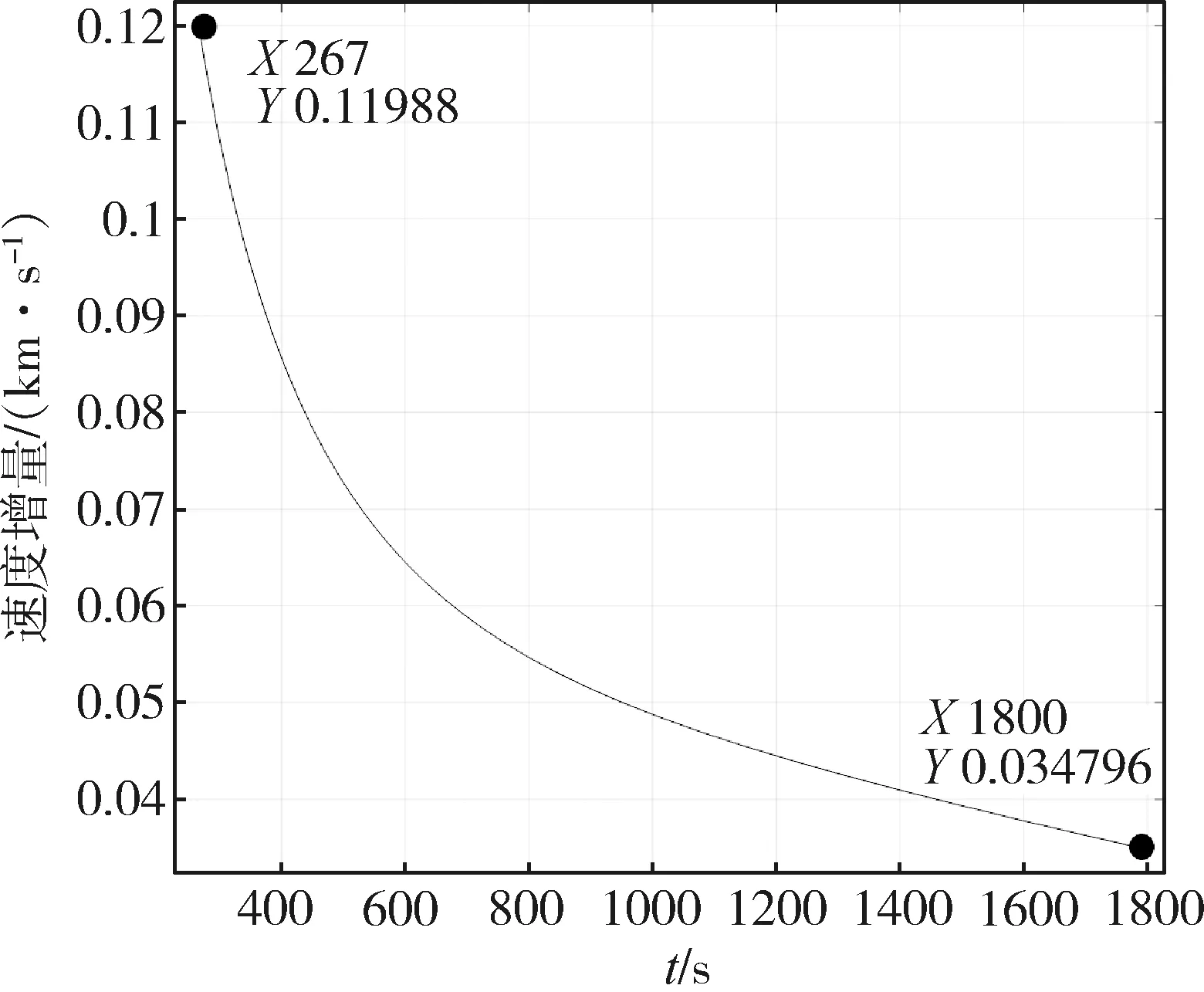
圖7 初始脈沖與攔截時間的關系曲線

令Δt=1800s，根據普適變量法得到無攝條件下的攔截軌道。從該軌道起點開始，通過GMAT軟件考慮J2項進行軌道積分，可得到終點的速度位置。從表3立方星在單脈沖下末端位置可以得到：在J2攝動影響下，攔截末端存在0.102km的脫靶量。由此可見，單次脈沖并不能滿足攔截精度要求，需通過二次脈沖減少脫靶量。

表3 J2攝動下的單脈沖末端位置

何時施加二次脈沖十分重要。一方面若施加脈沖過早，則攝動力對修正階段的影響會隨之增加，導致修正效果不佳；另一方面若施加脈沖過晚，則燃料消耗增多，故需在兩者間找到平衡。最終確定Δt1=0.95Δt，通過解式(9)，得到在t1時刻施加的脈沖及立方星的速度矢量δv+(t1)，得到第二次脈沖數據如表4。

表4 慣性坐標系下二次脈沖

兩次脈沖的攔截過程為：初始時刻立方星施加一次大小為34.796m/s的脈沖，進入攔截軌道實現慣性飛行。運行1710s后，兩航天器存在1.954km的相對距離。施加大小為2.43m/s的第二次脈沖，使立方星進入末段修正環節。兩次脈沖滿足燃料約束，該方案可行。

將實時位置導出與單脈沖情況作差，得到圖8的相對距離曲線。由圖8可以看出，在相應時間施加二次脈沖，可將位置誤差由1.0197×10-1km降低到5.1469×10-5km，提高了攔截精度。GMAT對應攔截過程如圖9所示。

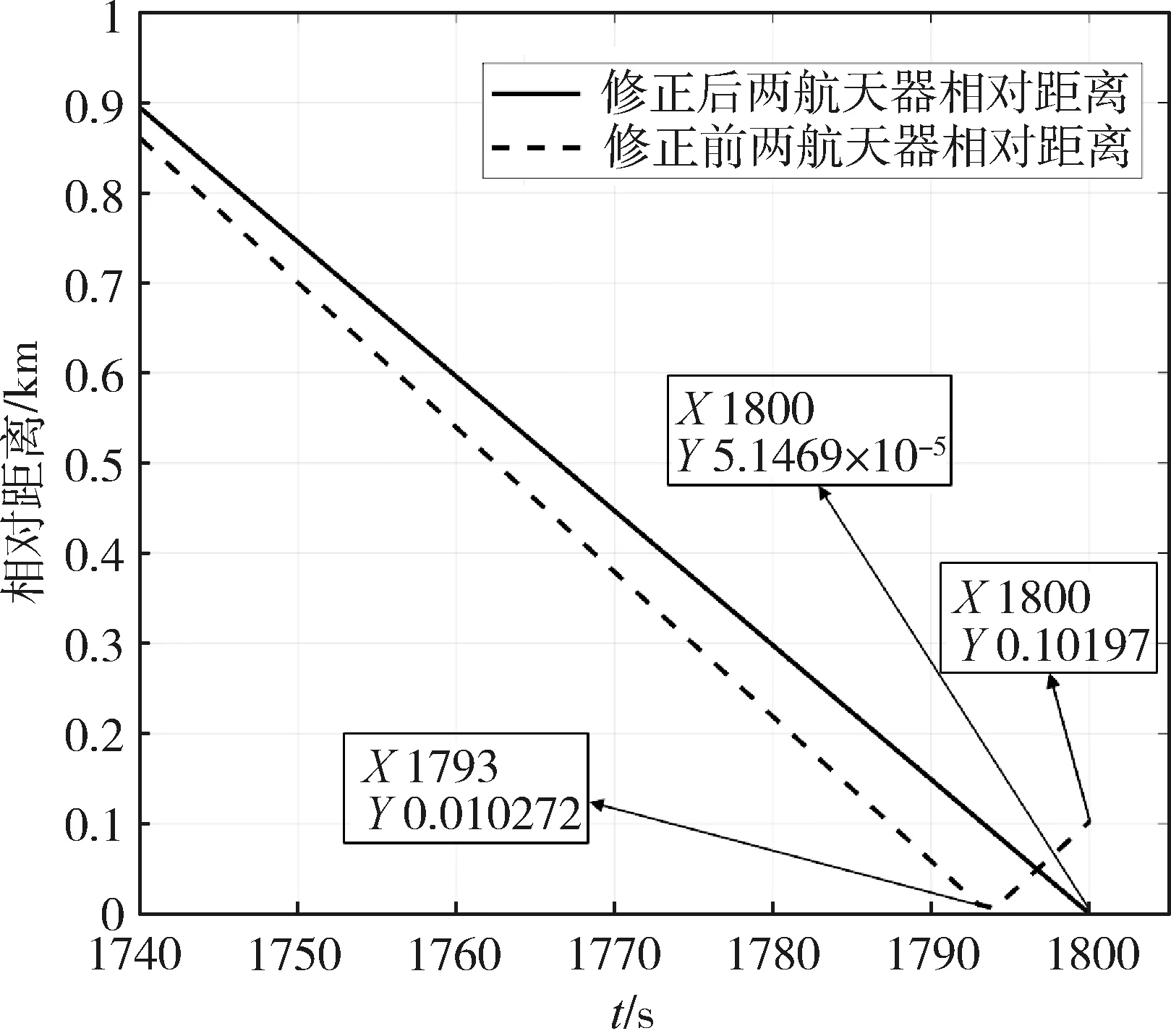
圖8 修正前后立方星與目標相對距離曲線

圖9 GMAT攔截軌道演示

5 結論

針對立方星攔截問題，本文提出了基于Lambert問題和C-W方程的二次脈沖攔截軌道設計方法，能夠在攝動環境下對目標實施有效攔截，并且給定時間內使得燃料消耗最少，可適用于多種場景。本文建立的GMAT/Matlab聯合仿真表明，該算法具有良好的末端攔截精度；鑒于時間和燃料消耗的評價指標，本文還給出了立方星在限定時間內的平面攔截域,分析了立方星在時間受限下的可攻擊范圍。上述工作為立方星這類能力受限的微小航天器動能末端攔截提供了思路。由于本文僅重點考慮低軌J2攝動下對無變軌目標的攔截，后續還可以加入其他攝動和追逃-攔截博弈算法，進一步完善立方星的攔截策略。