排列組合二項式定理綜合測試卷(B 卷)

■河南省南陽市二中 郭臣峰

一、選擇題

A.11 B.12 C.13 D.14

A.10 B.9 C.4 D.3

3.在一次運動會上有四項比賽的冠軍在甲、乙、丙3 人中產生,那么不同的奪冠情況共有( )種。

5.由0,1,2,5四個數組成沒有重復數字的四位數中,能被5整除的個數是( )。

A.24 B.12 C.10 D.6

6.將4張座位編號分別為1,2,3,4的電影票全部分給3 人,每人至少1 張。如果分給同一人的2 張電影票具有連續的編號,那么不同的分法數是( )。

A.24 B.18 C.12 D.6

7.從6 種不同的顏色中選出一些顏色給如圖1 所示的4個格子涂色,每個格子涂一種顏色,且相鄰的兩個格子顏色不同,則不同的涂色方法有( )。

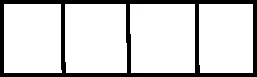
圖1

A.360種 B.510種

C.630種 D.750種

8.A、B、C、D4 名學生報名參加學校的甲、乙、丙、丁4 個社團,若學生A不參加甲社團,B不參加乙社團,且4名學生每人報一個社團,每個社團也只能1人報名,則不同的報名方法數為( )。

A.14 B.18 C.12 D.4

9.為了提高命題質量,命題組指派5 名教師對數學卷的選擇題、填空題和解答題這3種題型進行改編,則每種題型至少指派1名教師的不同分派方法種數為( )。

A.90 B.36

C.150 D.108

11.計劃展出10 幅不同的畫,其中1 幅水彩畫、4 幅油畫、5 幅國畫,排成一行陳列,要求同一品種的畫必須連在一起,并且水彩畫不放在兩端,那么不同的陳列種數為( )。

12.若(2+ax)n(a≠0)的展開式中各項的二項式系數之和為512,且第6項的系數最大,則a的取值范圍為( )。

A.49 B.-47 C.-1 D.1

14.包括甲、乙、丙3 人的7 名 同學站成一排拍紀念照,其中丙站正中間,甲不站在乙的左邊,且不與乙相鄰,則不同的站法有( )。

A.240種 B.252種

C.264種 D.288種

15.已知(3-x)(2x-3)8=a0+a1(x-1)+a2(x-1)2+…+a9(x-1)9,則a6=( )。

A.-1 792 B.1 792

C.-5 376 D.5 376

16.5名護士上班前將外衣放在護士站,下班后從護士站取外衣,由于燈光暗淡,只有2人拿到了自己的外衣,另外3 人拿到別人外衣的情況有( )。

A.60種 B.40種

C.20種 D.10種

17.停車場劃出一排9個停車位置,今有5輛不同的車需要停放,若要求剩余的4個空車位連在一起,則不同的停車方法有( )。

18.從正方體的8 個頂點中選取4 個作為頂點,可得到四面體的個數為( )。

20.羅馬數字是歐洲在阿拉伯數字傳入之前使用的一種數字,它的產生標志著一種古代文明的進步。羅馬數字的表示法如表1:

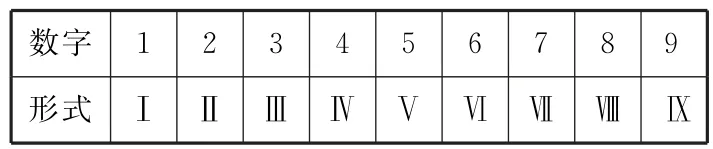
表1

其中“Ⅰ”需要1根火柴,“Ⅴ”與“X”需要2根火柴,若為0,則用空位表示,如123表示為,405 表示為。如果把6 根火柴以適當的方式全部放入圖2中,那么可以表示的不同的三位數的個數為( )。

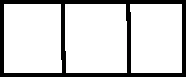
圖2

A.87 B.95

C.100 D.103

21.某龍舟隊有8名隊員,其中3人只會劃左槳,3 人只會劃右槳,2 人既會劃左槳又會劃右槳。現要選派劃左槳的3人、劃右槳的3人共6人去參加比賽,則不同的選派方法共有( )。

A.26種 B.30種

C.37種 D.42種

22.現有6 種不同的顏色,給圖3中的6個區域涂色,要求相鄰區域不同色,則不同的涂色方法共有( )。A.720種 B.1 440種C.2 880種 D.4 320種

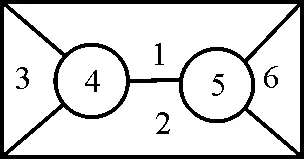
圖3

24.回文聯是我國對聯中的一種,用回文形式寫成的對聯,既可順讀,也可倒讀,不但意思不變,而且頗具趣味。相傳,清代北京城里有一家飯館叫“天然居”,曾有一副有名的回文聯:客上天然居,居然天上客;人過大佛寺,寺佛大過人。在數學中也有這樣一類順讀與倒讀都是同一個數的自然數,稱之為“回文數”。如44,585,2 662等。那么用數字1,2,3,4,5,6可以組成四位“回文數”的個數為( )。

A.30 B.36 C.360 D.1 296

25.將7個座位連成一排,安排4個人就坐,恰有兩個空位相鄰的不同坐法數為 ( )。

A.240 B.480 C.720 D.960

A.160 B.210 C.120 D.252

27.某高校需安排5 位應屆畢業生到3家企業實習,每家企業至少有1位實習生,并且實習生甲和乙必須去同一家企業實習,則不同的實習方式共有( )。

A.12種 B.18種

C.24種 D.36種

28.用數字0、1、2、3、4、5 組成沒有重復數字的四位數,則下列說法正確的是( )。

A.可組成360個不重復的四位數

B.可組成156個不重復的四位偶數

C.可組成198個能被3整除的不重復四位數

D.若將組成的不重復的四位數按從小到大的順序排成一個數列,則第85個數字為2 310

29.過三棱柱中任意兩個頂點的連線作直線,在所有這些直線中構成異面直線的對數為( )。

A.18 B.30 C.36 D.54

30.若(1+x)+(1+x)2+…+(1+x)n=a0+a1x+a2x2+…+anxn,且a1+a2+…+an-1=125-n,則下列結論錯誤的是( )。

A.n=6

B.(1+2x)n展開式中二項式系數和為729

C.(1+x)+(1+x)2+…+(1+x)n展開式中所有項系數和為126

D.a1+2a2+3a3+…+nan=321

二、填空題

31.已知m,n∈(0,+∞),若二項式的展開式中常數項為2 800,所有項的系數和為0,則

32.某單位在周一到周六的6天中安排4人值夜班,每人至少值一天,至多值兩天,值兩天的話必須是相鄰的兩天,則不同的值班安排種數為____。(用數字作答)

33.從1,3,5,7,9中任取2個數字,從0,2,4,6 中任取2 個數字,一共可以組成____個沒有重復數字的四位數。(用數字作答)

34.有7名同學站成一排照畢業紀念照,其中甲必須站在正中間,并且乙、丙2位同學要站在一起,則不同的站法有____種。

35.一排11個座位,現安排2人就座,規定中間的3個座位不能坐,且2人不相鄰,則不同排法的種數是_____。

36.9910被1 000整除的余數為_____。

38.將編號為1,2,3,4,5,6,7 的小球放入編號為1,2,3,4,5,6,7的7個盒子中,每盒放一球,若有且只有3個盒子的編號與放入的小球的編號相同,則不同的放法種數為____。

39.新冠肺炎疫情防控期間,為加大宣傳力度,提高防控能力,某縣疾控中心擬安排4名醫務人員到流動人口較多的3個鄉鎮進行疫情防控督查,每名醫務人員只去1個鄉鎮,每個鄉鎮至少安排1 名醫務人員,則不同的安排方法共有_____種。

40.用1、2、3、4、5、6、7、8 組成沒有重復數字的八位數,要求1與2相鄰,3與4相鄰,而7與8不相鄰,則這樣的八位數共有____個。

41.設a∈Z,且0≤a<13,若512021+a能被13整除,則a=_____。

42.直線方程Ax+By=0,若從0、1、3、5、7、8這6個數字中每次取2個不同的數作為A、B的值,則可表示_____條不同的直線。

43.將A,B,C,D,E這5名同學從左至右排成一排,則A與B相鄰且A與C之間恰好有1名同學的排法有____種。

45.經過班級同學初選后,將從5名男生和3名女生中選出4人分別擔任班長、學習委員、勞動委員,文藝委員。其中男生甲不適合擔任學習委員,女生乙不適合擔任勞動委員。現要求:如果男生甲入選,則女生乙必須入選。則不同安排方法的種數為____。

46.賈同學、王同學、文同學3 人在操場踢球,每次傳球,傳球者將球隨機將傳給另外兩位同學之一,足球最開始在文同學腳下,則:①n次傳球之后,共有____種可能的傳球方法;②n次傳球之后,足球回到文同學腳下的傳球方法有____種。

三、解答題

47.從1到7的7個數字中取2個偶數和3個奇數組成沒有重復數字的五位數。

試問:(1)能組成多少個不同的五位偶數?

(2)五位數中,2個偶數排在一起的有幾個?

(3)2個偶數不相鄰且3 個奇數也不相鄰的五位數有幾個? (所有結果均用數值表示)

48.某重點高中2022年五一演講比賽將在學校體育館舉行,所有參加人員憑票入場。

(1)若將6張連號的門票分給明明、慧慧等6位老師,每人1 張,且明明、慧慧分得的門票連號,則一共有多少種不同的分法?

(2)高二年級準備從甲、乙等8名同學中選派4名同學參加,要求甲、乙2名同學至少有1人參加,且若甲、乙同時參加時,他們的演講順序不能相鄰,那么高二年級不同的演講順序一共有多少種?

(1)求n的值;

(2)求展開式中含的項及展開式中二項式系數最大的項。

50.已知10件不同的產品中有4件是次品,現對它們進行測試,直至找出所有的次品為止。

(1)若恰在第5 次測試后就找出了所有次品,則這樣的不同測試方法數是多少?

(2)若恰在第2 次測試才測試到第1 件次品,第7次才找到最后一件次品,則這樣的不同測試方法數是多少?

52.第22 屆世界杯足球賽于2022 年夏季在卡塔爾舉辦,五大洲共有32支球隊有幸參加。他們先分成8 個小組進行循環賽,決出16強(每隊均與本組其他隊賽一場,各組第一、第二名晉級16 強),這16 支球隊按確定的程序進行淘汰賽,最后決出冠亞軍,此外還要決出第三、第四名,問這屆世界杯總共進行了多少場比賽。

53.從包括A、B兩人的7個人中選出5人排成一排。

(1)若任意選5 人,有多少種不同的排法?

(2)若A、B兩人中有且只有一人在內,有多少種不同的排法?

(3)若A、B兩人都在內且A、B不相鄰,有多少種不同排法?

(4)若排頭和排尾不允許站A,正中間(第三位)不允許站B,有多少種不同的排法?

(1)求展開式中所有的有理項;

(2)求展開式中系數最大的項。

55.(1)6 個人從左至右排成一排,最左端只能排甲或乙,最右端不能排甲,則不同的排法共有幾種? (最后結果需用數字作答)

(2)把5件不同產品擺成一排,若產品A與產品B相鄰,且產品A與產品C不相鄰,則不同的擺法有幾種? (最后結果需用數字作答)

(3)4個不同的小球放入編號為1,2,3,4的4個盒子中,恰有1個空盒,共有多少種放法? (最后結果需用數字作答)