巧借問題表征之力驅動數學建模能力

徐冰 山東省東營市實驗小學

問題表征是指在頭腦中對一個問題信息進行記載、理解和表達的方式。數學表征能力是數學解決問題過程的一個重要階段，恰當的問題表征是成功解決問題的前提條件。

一、問題表征的內涵

隨著科學技術的不斷進步，數學廣泛滲透在人們的日常生活中，“大眾數學”的倡導使得“能夠準確形象地用合適的表征方式表達數學”顯得格外重要。“表征系統”這一概念是由美國學者首次提出的。新加坡數學課程標準（2007 年）中提出：在問題解決和探索中使用直觀表征，比如模型、圖表、圖像、圖形等。在我國，問題表征在數理化應用題中的研究比較早，徐明（2002 年）將數學問題的外在表征形式分為了五類：文字表征、數式表征、圖表表征、模型表征和實驗表征。

問題表征，是數學問題在學生頭腦中的理解、呈現、表達和記載方式。問題表征能力是指在問題解決過程中，學生綜合運用觀察、操作、分析、綜合等思維方式，將“數學問題所包含的有效信息”同“自身儲存的知識經驗”進行主動建構，促進“數學問題”轉化為“圖像模型”“符號模型”等數學模型，并應用模型解決問題的一種思維能力。問題表征能力是數學建模能力的核心。問題表征能力的強弱決定著學生對數學問題的理解程度，決定著學生問題解決能力的發展水平。也就是說，如果一個數學問題得到了恰當的表征，那么這個問題就解決了一半。

本文從數學建模的角度出發，將“問題表征”與“解決問題”有機地聯系在一起，在課堂中鼓勵學生用多種表征方式解決問題，譬如借助情境、語言、圖形、符號等可以幫助學生理解題意，形成解決問題的思考方法，從而培養學生多元化的數學表征方式，提高學生的數學表征水平，并通過對比、分析、抽象順利建立數學模型，從而解決數學問題，發展學生的數學建模能力。皮亞杰認為：“7～11 歲兒童的認知結構由前運算階段的表象圖式演化為運算圖式。該時期的心理操作著眼于抽象概念，屬于運算性（邏輯性）的，但思維活動需要具體內容的支持。”因此，在教學過程中，教師要引導學生用圖形、符號、表格等方法表征問題，從而支持學生的思維活動，把抽象的數學問題直觀化、具體化，促進“數學問題”轉化為“圖形模型”“符號模型”等數學模型，有助于學生探索解決問題的思路和方法，提升數學建模能力。

二、問題表征在數學問題解決中的教學實踐

（一）圖形表征

圖形表征是有效構建數學模型必不可少的表征方式。在具體的教學實踐中，當學生遇到抽象難懂或復雜難解的數學問題時，可以通過“實物圖”“示意圖”“線段圖”等多種方式，將抽象的“數學問題”轉化為直觀的“圖形模型”，使抽象的“數學問題”直觀化、形象化、模型化。同時，這一過程能夠發展學生的具體形象思維和抽象邏輯思維能力，增強學生的問題解決能力和數學建模能力。

圖形表征有利于學生由直觀形象思維逐步向抽象思維過渡，從而突破教學內容中的關鍵問題或疑難問題。借助圖形表征，學生可以梳理數量關系，順利建構數學模型。

【案例1】求比一個數多幾的數（青島版數學五四制二年級下冊第67頁）

1.問題情境

學生根據情境圖找信息、提問題：黃鸝有46 只，喜鵲比黃鸝多8只，黃鸝有多少只？

2.建立模型

師：你能用畫一畫的方法將信息和問題整理一下嗎？

（1）學生嘗試用畫一畫的方法整理信息和問題。

（2）展示交流。

第一種方法：

用46 個小圓圈表示黃鸝的只數，下面一行圓圈表示喜鵲的只數。多出的圓圈，表示喜鵲比黃鸝多的只數。

第二種方法：

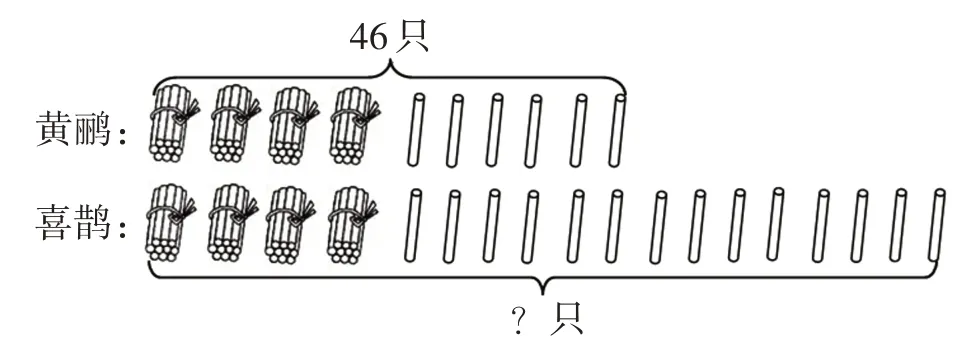
師：對比第一種方法和第二種方法，你更喜歡哪一種呢？

生：我更喜歡第二種方法，因為第一種方法一個一個畫太麻煩了。

第三種方法：

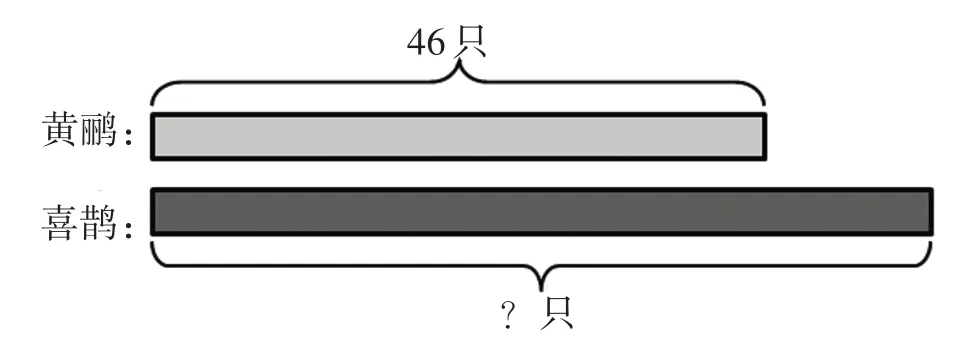
生問：多的8只在哪里呢？

師：怎樣畫一畫讓別人一眼看出多8 只呢？誰有辦法？

（一學生到投影下畫一畫）

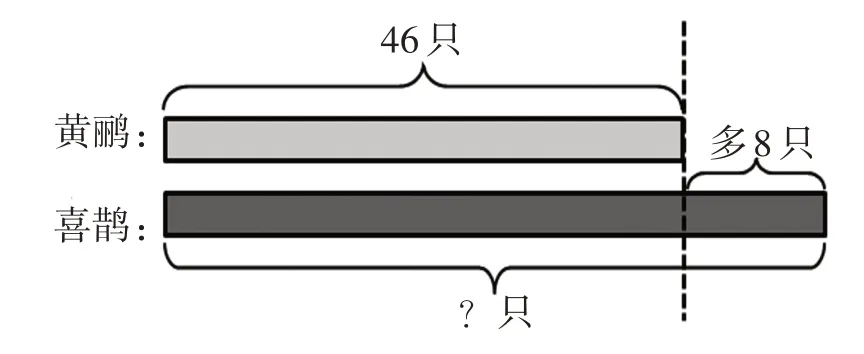
師：這條虛線真巧妙，把喜鵲的只數分成了兩部分，是哪兩部分呢？誰能結合圖說一說呢？

生：虛線前面的是“和黃鸝同樣多的部分”，虛線后面的是“比黃鸝多的部分”。

師：再來對比第二種方法和第三種方法，你更喜歡哪一種方法呢？

生：我更喜歡第三種方法，因為這樣畫一個直條更方便了，數多大都可以。

（3）借助直條圖，解決問題（略）

3.拓展應用

師：還是這個直條圖，你能根據這個直條圖編一個數學故事嗎？

生1：我們班有男生20 人，女生比男生多5 人。女生有多少人？

生2：我的體重是35 千克，媽媽比我重20 千克。媽媽的體重是多少千克？

生3：……

德國數學家戴維·希爾伯特在其著作《直觀幾何》一書中提到：“圖形可以幫助我們發現、描述研究的問題，也可以幫助我們尋求解決問題的思路，還可以幫助我們理解、記憶所得到的結果。”由此可見，圖形對于解決數學問題而言非常重要，利用圖形可以化抽象為形象，幫助學生提升抽象邏輯思維能力。因此，在本案例中，教師放手讓學生用多種方法來表征數量關系，并對這些方法進行了兩次對比，第一次對比是一個一個畫和十個十個畫之間的對比，你喜歡哪一種？學生會清楚地看到一個一個畫太麻煩了，從而感悟第二種方法的簡便性。第二次對比是十個十個畫和直條圖之間的對比，你更喜歡哪一種？有了第一次對比的經驗，學生自然會想到，如果數更大，十個十個畫也很麻煩，而一個小直條不僅可以表示46 只喜鵲，也可以表示460 只喜鵲，甚至可以表示更大的數，從而使學生感悟到直條圖表示數量的簡便性。小學生的思維發展離不開直觀的支撐，所以在本案例中，利用直條圖幫助學生感悟抽象的數量關系，在對比中逐步建立數學模型，學生的問題解決能力由此得到有效培養，此后解決“比一個數少幾的數”的問題就水到渠成了。

（二）符號表征

所謂“符號表征”是指將數學問題中的信息或關系抽象為用數學符號表示的算式、公式、字母式等，借以分析和解決數學問題。符號表征是分析關系和解決問題必不可少的一種表征方式。

【案例2】搭配問題（青島版數學五四制二年級下冊第34-35頁）

1.問題情境

學生根據情境圖找信息、提問題：2 件上衣、3 條裙子。一件上衣和一條裙子任意搭配，有幾種不同的穿法？

2.建立模型

（1）探究：用擺一擺、寫一寫、畫一畫等方法探索搭配方法。

（2）匯報交流，講解自己的方法，建立模型。

（3）對比優化。

師：這么多的方法，你更喜歡哪種方法呢？

生1：我喜歡用圖形表示的，這樣很方便。

生2：我喜歡用字母表示的，寫起來很簡單。

師：對啊，寫字、畫實物圖的方法都很麻煩，在數學中我們經常會用一些符號來代替實物或者文字，這樣就簡單多了。

（4）借助符號模型，解決問題

師：一共有多少種搭配方法呢？

生1：我數了數一共有6 條線，所以有6 種搭配方法。

生2：2×3=6（種）

3.拓展應用

（1）早餐搭配：3 種飲料，4 種點心。一種飲料配一種點心，有多少種不同的吃法？

（2）學生獨立思考，在作業本上畫一畫、連一連。

（3）展示部分學生的方法，說一說自己的搭配方法。（略）

建立符號意識有助于學生理解符號的使用是數學表達和進行數學思考的重要形式。在本案例中，教師給學生提供了衣服圖片的學具，學生可以借助圖片擺一擺、畫一畫、寫一寫。通過對比，學生感受到用符號代替實物的簡便性。“符號”鋪就了模型建立之路，提升了學生的數學建模能力。

（三）表格表征

所謂“表格表征”是指將數學問題中的信息或關系抽象化為圖表，借以輔助分析和解決問題。表格表征是直觀呈現數量關系模型、有效解決問題的一種輔助性工具和策略。表格簡單明了，有助于分析比較復雜的數學問題，發現規律，建立模型。

【案例3】解決問題的策略——表格列舉法（青島版數學五四制一年級下冊第75-76頁）

1.問題情境

學生根據情境圖找信息、提問題：從第一天開始種1棵樹，以后每天比前一天多種1棵樹。4天一共要種多少棵樹？

2.建立模型

師：請大家用自己喜歡的方法把信息表示出來，寫在作業本上。完成后和同桌交流一下你的想法。

（1）自主探究。

（2）匯報展示，建立模型。

（3）對比優化

師：對比這幾種方法，它們有什么相同點和不同點？

生1：這些方法都是把每一天有幾棵都列出來了。

生2：有的方法是寫數字，有的方法是畫一畫。

師：這些方法，你更喜歡哪一種呢？為什么？

生：我更喜歡第三種，因為前兩種還得去數一數每天有多少棵。

師：是啊，如果100 天一共種了多少棵數，我們去畫一畫，你們覺得怎么樣？

生1：很麻煩，畫很長時間。

生2：直接寫數簡單，一眼就看出每天種了幾棵。

師：通過大家的對比，我們發現第三種方法簡單、清楚。第三種方法你們能看明白嗎？

師：這四行分別表示什么呢？（用黑色彩筆畫出4行，第一天1棵，第二天2棵，第三天3棵，第四天4棵）

生：第一行表示第一天種的棵數，第二行表示第二天種的棵數，第三行表示第三天種的棵數，第四行表示第四天種的棵數。

師：說得真清楚。那這兩列又分別表示什么呢？（天數和棵數分為2列）

生：第一列表示天數，第二列表示每天種的棵數。

師：看，我們給第三種方法加上了表格，你能給這種方法起個名字嗎？

生：表格法。

師：我們在表格里，把每天種的棵數都列舉出來了，這種方法在數學上叫表格列舉法。

（4）借助表格，解決問題

師：這個“表格列舉法”非常清楚、明白，方便我們解決問題。根據表格中列舉的信息，你會計算4 天一共種了多少棵樹嗎？

生：1+2+3+4=10（棵）

3.拓展應用

一本書一共有64頁。小嬌周日看了6頁，以后每天比前一天多看2頁，周五時她能看完這本書嗎？

師：請大家獨立完成，完成“作業單”。

（1）學生獨立列表格解決問題。

（2）展示、匯報。（略）

本案例中，學生第一次接觸列表格整理信息，解決問題，以前接觸的都是根據文字或現成的表格，直接列算式解決問題，所以“表格法”對學生來說有一定的挑戰。基于學生的認知水平，本案例中，首先，放手讓學生自主表征問題，通過對比“它們有什么相同點和不同點”體會畫圖和表格法之間的聯系，讓表格法的學習有所依托。其次，“你更喜歡哪種方法？”學生會感悟到使用表格法不僅可以清楚地看到數據，還可以看出數據的變化規律，從而能快速地解決問題。最后，教師沒有著急告訴學生“第三種方法我們畫上線，這就是表格法”，而是通過“這四行分別表示什么呢？”“那這兩列又分別表示什么呢？”這兩個問題的引領，使表格躍然紙上。這樣的制表過程，逐步引導學生經歷了表格的形成過程，有利于學生讀懂表格，從表格中抽象出基本的數量關系，建立模型，把握同一類型問題的解題策略。

總之，問題表征在數學問題解決中具有重要促進作用，對改善學生的學習方式，優化學生的數學思維結構等有促進作用，應該在日常數學學習中引起重視。