淺談轉化思想在初中數(shù)學解題教學中的有效應用

邵劍飛

（甘肅省會寧縣黨家峴鄉(xiāng)初級中學，甘肅會寧 730700）

在新課改后，教師逐漸將教學重心由講述理論知識轉變?yōu)榕囵B(yǎng)核心素養(yǎng)，以潛移默化的方式，幫助學生提升自身的邏輯思維和創(chuàng)新思想。在數(shù)學學習中，轉化思想是一種常用的、能夠幫助學生解決疑難問題和復雜問題的方法，能夠拓展學生的思維，培養(yǎng)學生的數(shù)學核心素養(yǎng)。因此，在數(shù)學教學中，教師應提升學生對數(shù)學學科的興趣和愛好，激發(fā)學生的自主研究和探索精神，引導學生積極運用轉化思想解決問題，有效提升初中數(shù)學的教學效率。

一、轉化思想的定義與轉化方法

（一）轉化思想的定義

轉化思想，廣義上是指受外部因素和內在因素的影響，人在思想方面的轉變；在數(shù)學解題中，具體是指教師通過創(chuàng)新教學方式，轉化學生的內在思想，從而有效開展課堂教學。簡單來說，轉化思想就是將新舊知識相銜接，從多種角度進行思考，另辟蹊徑。靈活應用轉化思想，在解題過程中能夠正確解決難度較高的證明題和應用題，從而提升學生對初中數(shù)學學習的自信心。轉化思想以發(fā)散性思維為基礎，利用學生頭腦中的認知改變，讓學生的思想進行內部轉化，對解題的方向、強度進行靈活的變化，以新思想代替舊思想，取得良好的解題效果。

在轉化思想過程中，教師應注意學生在解題過程中的量變和質變，從轉化思想中的順從、認同和內化出發(fā)，引導學生完成從被動轉變思想到自主轉化解題思路的思想態(tài)度轉變，從而實現(xiàn)學生對轉化思想的認同，最終完成轉化思想的質變過程。學生一旦將轉化思想內化為自己的思想，轉化思想在解題過程中的應用就會更加高效，而這也突出了學生在解題過程中的主觀作用，實現(xiàn)由被動到主動、由主動到自覺的學習過程。因此，在初中數(shù)學解題教學中，教師應積極運用轉化思想，引導學生積極主動地思考，尋找突破口，準確切入復雜的問題，將問題簡單化、分散化，逐級突破，從而培養(yǎng)學生的邏輯思維能力，為學生的未來學習和發(fā)展奠定良好的基礎。

（二）在初中數(shù)學解題教學中的轉化方法

在當前的初中數(shù)學解題教學中，存在多種思想轉化方法，教師應根據(jù)學生的學習特點，篩選出合適的轉化方法，以實施分層次的數(shù)學解題教學。

第一，類比轉化思想。類比方法，即將類似的、相近的事物進行轉化，注重解題方法和解題步驟的同化，從而讓學生能夠在面對新授課時得心應手。例如，在學習初中數(shù)學一元一次不等式時，教師可以引導學生將題目類比轉化成為一元一次方程的解題過程，根據(jù)已掌握的方程知識解決遇到的不等式問題。

第二，語言轉化思想。數(shù)學應用題以語言描述為主，教師可以引導學生將數(shù)學公式或者基本法則轉化成為生活中的語言，或者將幾何題中的符號及圖形進行語言轉化，這樣表達更貼近學生的生活實際，有利于學生將數(shù)學理論知識與實踐相結合，有效解決生活中的問題。

第三，數(shù)形轉化思想。在初中數(shù)學解題過程中，圖形與數(shù)字相結合，將數(shù)學題中的數(shù)字圖形化，能夠有效降低數(shù)學題的難度。例如，在解答數(shù)學問題時，可以在建立方程式的過程中，利用圖形進行轉化。如在研究正比例函數(shù)和反比例函數(shù)時，也可以用圖形表達題目中的信息，從而將抽象的理論知識具象化。

第四，分解轉化思想。面對比較復雜的初中數(shù)學問題，學生應具備一定的分解轉化思想，將大問題分割成為小問題，從而將復雜的問題簡單化。例如，在進行整式的加減乘除運算時，可以利用數(shù)學分解轉化思想，將題目分解成為數(shù)個簡要的題型，對整式進行分模塊計算，從而靈活運用多種解題方式。

二、轉化思想在初中數(shù)學解題教學中的有效應用

（一）實施分層次轉化思想，有效解決數(shù)學方程問題

初中數(shù)學的最大特點是以數(shù)量關系反映客觀世界，將空間形式進行對立統(tǒng)一的矛盾轉化。方程問題是初中數(shù)學的學習重點，不僅涉及基本的數(shù)量關系，還涉及多個變量。因此，在解方程的過程中，教師要有效運用轉化思想，引入加減消元法和代入法，將多個變量關系轉化為一個變量，引導學生運用已經掌握的知識點進行分析，能夠有效提高學生解決數(shù)學方程問題的正確率。

教師在實施轉化思想時，應根據(jù)學生的性格特征和學習習慣等，合理控制數(shù)學方程問題的難度，采取分層次的轉化思想，有效促進學生實現(xiàn)個性化的全面發(fā)展。此外，教師還應培養(yǎng)學生對方程問題的觀察力，在教學的過程中引導學生準確運用消元方法對題目進行變通，從而實現(xiàn)解決數(shù)學方程問題的新課改目標。例如，在分析二元一次方程組題目“有甲乙兩數(shù)，其和是9，其中乙數(shù)是甲的2 倍，求兩數(shù)各是多少”時，教師應先給學生講授基本的列方程的步驟：

假設甲數(shù)為x，乙數(shù)為y，那么可以將文字式的數(shù)學題轉化為方程組：（1）x+y=9（2）y=2x。因x 表示甲數(shù)是固定的，y 表示乙數(shù)也是固定的，因此，方程（1）中的y 可以用方程（2）中的2x 來表示。將方程（2）代入方程（1）中，從而得出x+2x=9 的一元一次方程，最終得出x=3 的正確答案。再將x=3 代入方程（2）中，得出y=6。將這個二元一次方程組進行整合，從而得出該方程組的解：x=3，y=6。

在以上解題過程中，應用到了消元和代入消元的轉化思想，教師應根據(jù)學生對二元一次方程組的掌握程度，采取針對性的轉化思想，為學生設置不同難度的方程應用題，從而提升學生解答二元一次方程組的正確率。在題目解答結束后，教師應將x=3、y=6 代入方程組中進行驗證，培養(yǎng)學生在落實轉化思想中的反思思維，從而確保答案的正確性。

在該二元一次方程組的解答中，教師應教授學生基本的轉化思想，要求學生在分析題意的基礎上，將方程中的一個未知數(shù)與另一個未知數(shù)相結合，并將另一個未知數(shù)利用正確的代數(shù)式表示出來，再次代入另一個方程中消去未知數(shù)，從而實現(xiàn)轉化思想在數(shù)學方程題目中的應用，將復雜的二元一次方程轉化為簡單的一元一次方程。

在初中數(shù)學題目中，轉化思想不僅僅局限于二元一次方程組中，還可以滲透到一元二次方程中。教師可以引導學生利用公式，以開平方、因式分解法等多種方法，將一元二次方程以降次的方式轉化為一元一次方程，從而降低方程式的難度，讓學生分層次掌握正確解答數(shù)學方程式的有效轉化思想。

（二）利用數(shù)形轉化思想，高效解決圖形問題

數(shù)字和圖形雖然是兩種差異性的表現(xiàn)形式，但是數(shù)字與圖形之間可以進行相互之間的轉化，利用數(shù)形轉化正確解答初中數(shù)學應用題。

首先，從圖形中尋找數(shù)量關系。初中數(shù)學應用題中有很多圖形題目，即利用已知的圖形解答相關的問題。教師應引導學生利用已學過的知識迅速找出表示圖形的數(shù)量關系，將初中幾何的相關問題代數(shù)化，從而尋找到問題的正確答案。例如，在學習復數(shù)及其相關運算時，學生可以利用復數(shù)中的幾何關系進行展示；在學習函數(shù)及其相關圖像的關系時，可以將圖形轉化為函數(shù)關系，從而提高解題效率。

其次，將數(shù)量關系以圖形的方式進行展示。在當前的初中數(shù)學題目中，經常以圖形的方式掩飾其是代數(shù)問題的本質，教師要引導學生仔細觀察，從圖形中發(fā)現(xiàn)數(shù)量關系，挖掘出數(shù)與形之間的內在關系，從而將幾何問題轉化成代數(shù)問題。如下題：

四邊形ABCD 是直角梯形，AB=8cm，∠B=90°，AD=24cm，BC=26cm。點P 作為一個移動點，從A 出發(fā)，以1cm/s 的速度移動，方向為D 點；點Q 從C 出發(fā)，以3cm/s 的速度移動，方向是B 點。點P 與點Q 同時運動，其中一個點到達線段終點時，兩個點同時停止運動，那么從運動開始，在多少秒之后，四邊形PQCD 能夠成為等腰梯形。

圖1

在解這道應用題時，應將問題假設成為已知條件，假設PQCD 是平行四邊形，根據(jù)平行四邊形的性質，對邊平行且相等，則可以得出結論：兩條對邊PD=CQ。從運動開始到運動結束，點P 運動的路程用箭頭來表示，可以明確指定為AP，點Q運動的路程用相反方向的箭頭來表示，可以顯示為CQ，因為平行四邊形的上下邊平行，所以可以得出：AP+CQ=AP+PD=AD，即兩個點的運動路程可以轉化為直角梯形的一條邊。再利用題目中的已知條件，可以將四邊形的問題轉化為行程問題，將兩個點的運動軌跡轉化為行程，利用代數(shù)中的行程應用題解題思路進行簡單的計算。將幾何圖形問題轉化為代數(shù)問題，使得復雜的問題簡單化，最終得出這道應用題的正確答案：在經過7 秒后，四邊形PQCD 能夠成為等腰梯形。

（三）堅持“以生為本”，實施化抽象為具體的轉化措施

“以生為本”的理念，即堅持學生在課堂中的中心地位，教師充分發(fā)揮“引導”“幫助”的作用，以實現(xiàn)學生的主體性，一切從學生的學習實際出發(fā)，從而促進學生全面發(fā)展。初中生正處于形象思維向抽象思維轉化的關鍵期，受年齡和身心發(fā)展規(guī)律的影響，抽象思維能力比較弱。尤其是學習能力較差的學生，面對邏輯性較強的問題時往往會產生抵觸心理，不能正確理解題目中的已知條件。因此，在初中數(shù)學解題教學中，教師應貫徹落實“以生為本”的教學理念，采取多元化的方法轉化思想，促使學生樹立正確的轉化意識，用直觀具體的方式理清解題思路，從而正確解決數(shù)學題目。比如在學習一次函數(shù)相關知識時，教師應從學生的學習基礎出發(fā)，將函數(shù)問題直觀表達為自變量之間的問題，借助數(shù)形結合思想，將邏輯性較強的問題轉化為學生可以理解的具體問題，從而激發(fā)學生對數(shù)學題目的探究積極性。例如，已知y1=x+m（m 為常數(shù)）的函數(shù)圖像與反比例函數(shù)y2=k/x（x≠0）的圖像相交于點A（1，3）。根據(jù)以上已知條件，求兩個函數(shù)的解析式及另一交點B 的坐標。并嘗試寫出函數(shù)值y1＞y2的自變量的取值范圍。（見圖2）

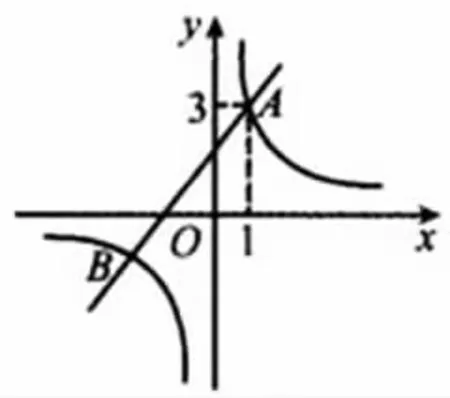
圖2

對于絕大多數(shù)學生來說，第一個問題并不難，將點A 的坐標代入函數(shù)式，就能夠得出兩個函數(shù)的解析式；將解析式組成方程組進行數(shù)值運算，就可以得出點B 的坐標。而在思考第二個問題時，學生應靈活運用轉化思想，將抽象的函數(shù)值數(shù)量關系知識轉化為具象的直角坐標系知識，充分發(fā)揮數(shù)形結合的作用。根據(jù)圖2 所示的直角坐標系，可以直觀地表達出y1＞y2的取值范圍，最終得出結論：當-3＜x＜0 或者x＞1時，函數(shù)值y1＞y2。因此，將抽象的函數(shù)值問題轉化為圖像問題，能夠清晰地描述并理清解題思路，并將復雜的問題簡單化，以潛移默化的方式培養(yǎng)學生的轉化思想，有效解決初中數(shù)學問題。

“以生為本”的教學理念是貼近學生生活實際的正確教育觀念，不僅有利于創(chuàng)設高效的初中數(shù)學課堂，還有利于培養(yǎng)學生的核心素養(yǎng)，從而實現(xiàn)新課改的素質教育目標。因此，教師應堅持以學生為中心的教學理念，結合學生的邏輯思維發(fā)展水平和創(chuàng)新能力水平，采取轉化思想，將抽象的數(shù)學問題轉化為具體的問題，并向學生直觀、形象地展示，從而培養(yǎng)學生對初中數(shù)學學科的興趣，積極探究數(shù)學學科的奧秘。

綜上所述，轉化思想對學生的數(shù)學學習以及邏輯思維的建立有著重要影響，在實際教學過程中，教師要通過對各種題型的練習和鞏固，使學生能夠熟練掌握這一應用技巧，從而內化于心、外化于形。教師應結合初中生的學習習慣，結合具體的案例分析，引導學生進行發(fā)散式的思維聯(lián)想，從而找到轉化思想應用中正確的切入點，實施分層次轉化思想，有效解決數(shù)學方程問題。教師還要落實因材施教原則，引導學生有效運用數(shù)形轉化思想，堅持“以生為本”教學理念，實施化抽象為具體的轉化措施，正確地分析問題、論證問題，擴展學生的思維，最終實現(xiàn)化繁為簡、巧妙解題的課堂教學目標。