一道中考題的探究*

廣東省深圳市光明區華夏中學 (518107) 蔣紅珠

華南師范大學數學科學學院 (510631) 黃文麗

內江師范學院數學與信息科學學院 (641100) 劉成龍

試題再現(2020年深圳中考第16題(下文簡稱16題))如圖1，已知四邊形ABCD，AC與BD相交于點

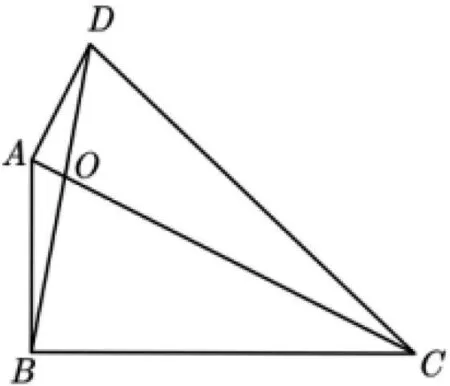
圖1

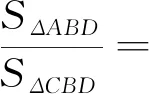
16題以直角三角形構成的四邊形為載體，主要考查學生對常見相似三角形相關模型的掌握程度，考查學生對面積比問題的轉化與解決能力，具有言語直觀、構思精巧、圖形簡潔、內涵豐富、背景公平、解法多樣等特點，是考查學生邏輯推理、直觀想象、數學建模、數學運算等素養的有力素材．同時，16題是數學探究的良好素材．下文將從試題的背景、解法和變式三個視角進行探究．

1 背景探究

研究試題背景可以準確把握試題的本質、理解試題的設問、擴寬試題的解法、加強試題的擴展．中考數學壓軸題追求試題背景的新穎性與獨特性，常常是在“教材知識”的基礎上向四大背景上集中：高中數學背景、現實生活背景、歷史名題背景、經典試題背景(包括往年的競賽題或中考題)．16題蘊涵教材背景和競賽背景．

背景1教材背景

源于北師大版九年級上冊第三章《圖形的相似》復習題中的第22題(第107頁):

第22題如圖2，AB⊥BD，CD⊥BD，AB=6，CD=4，BD=14，點P在BD上移動，當以P，C，D為頂點的三角形與ΔABP相似時，求PB的長．

評注：第22題中當以P，C，D為頂點的三角形與ΔABP相似時，就可提煉出“一線三等角模型”中的“一線三直角模型”，是相似三角形中的重要模型．在16題的圖1中，過點D作BC的平行線與BA的延長線交于點E，如圖3所示，通過16題的其他條件可知∠E=∠ABC=∠DAC=90°，即含有“一線三直角模型”．命題者間接選擇“一線三直角模型”為素材，為ΔABD和ΔCBD求面積找底和高奠定了基礎，考查學生轉化與化歸思想及數形結合思想．

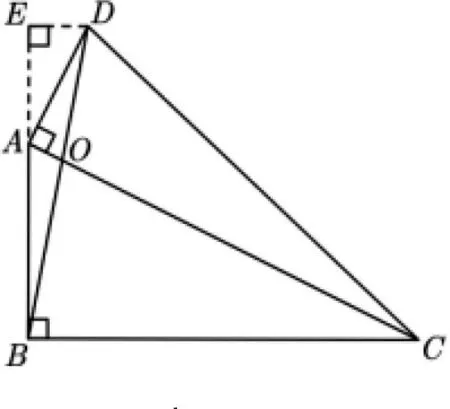
圖3

背景2競賽背景

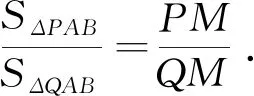
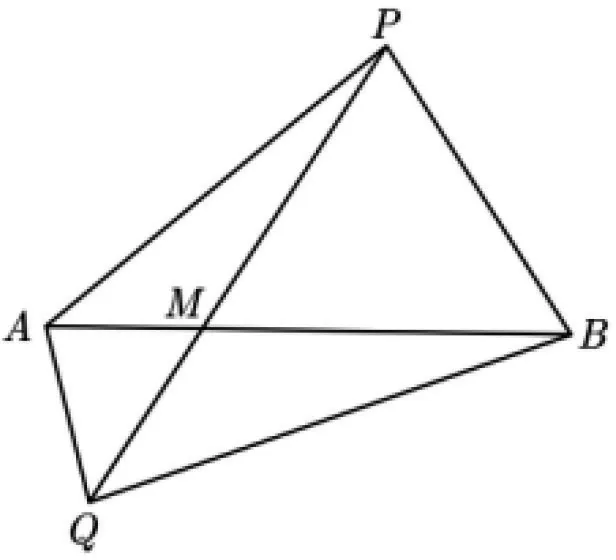
(1)

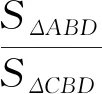
2 解法探究

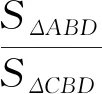
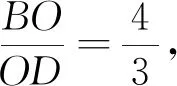
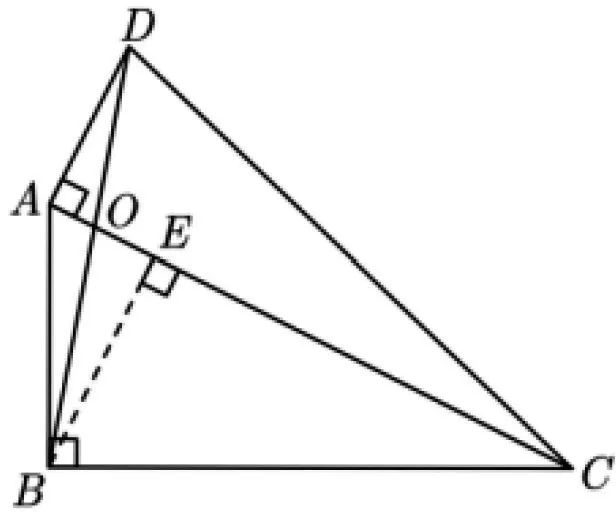
圖5

評注：解法1主要使用了相似三角形的性質來解答問題，解法1后面求OC時，也可使用射影定理來求．

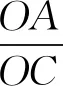
解法2：如圖6，過點D作BC的平行線與BA的延長線交于點E，過點O作AB的垂線交AB于點F，由∠ABC=∠DAC=90°，則易證ΔAED～ΔOFA～ΔCBA且ΔAFO～ΔDEB．因為

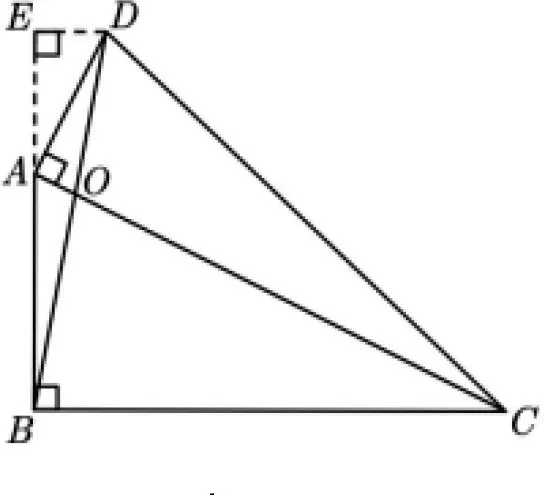
圖6

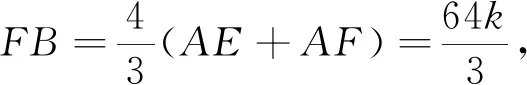
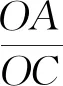
思路3 解法1和解法2都主要通過相似三角形的性質來解答的，而構造相似三角形的一個重要方法就是作平行線，構造“8”字模型．

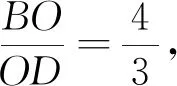
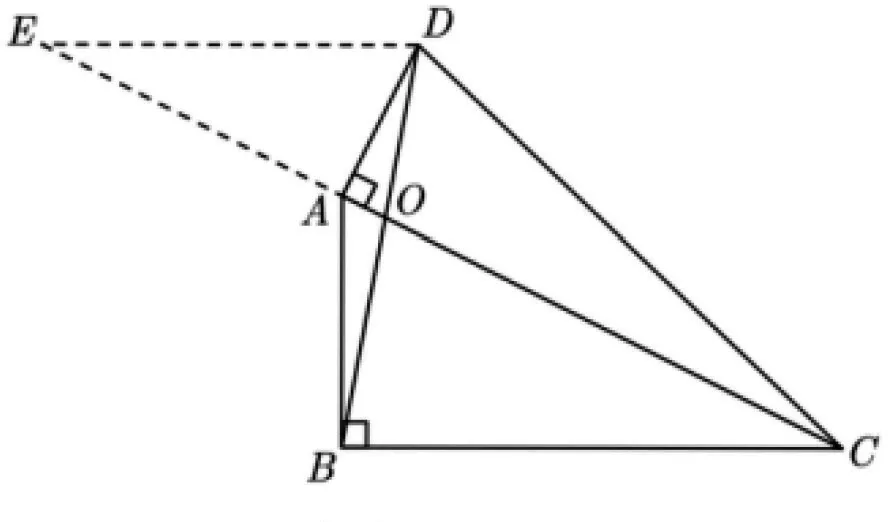
圖7

評注：解法3利用作平行線構造相似三角形，在求解OA與OC的比值過程中主要使用方程的思想．

思路4 求兩個三角形的面積之比時，更為直接的想法是用底和高的乘積將其表示出來．

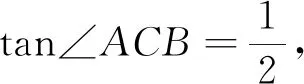
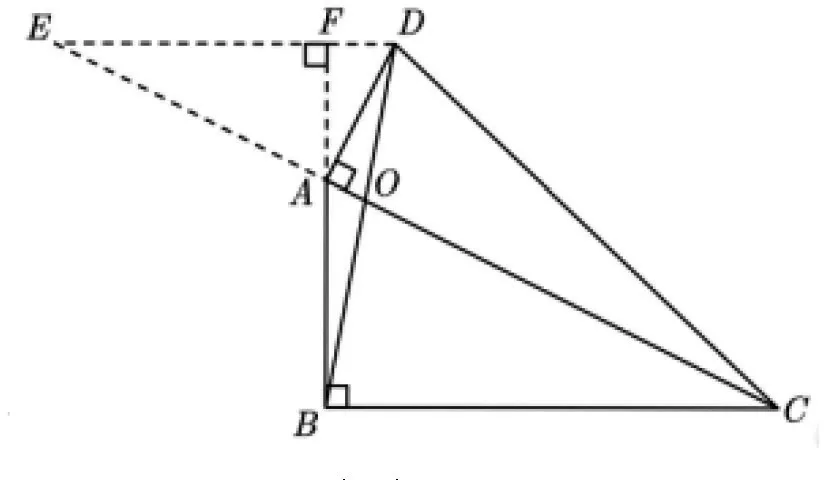
圖8

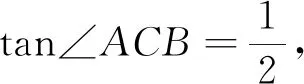
評注：解法4和解法5解答原理一樣，只是尋找ΔABD和ΔCBD不同的底和高而已．

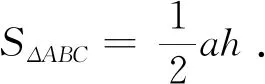
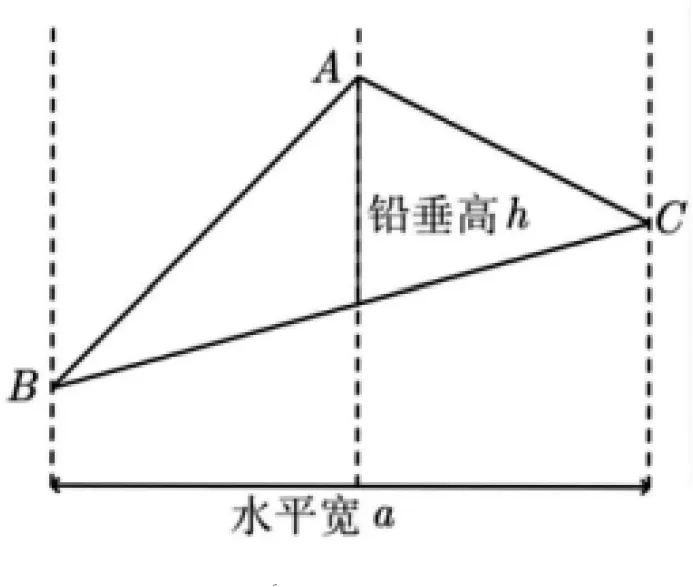
圖9

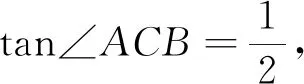
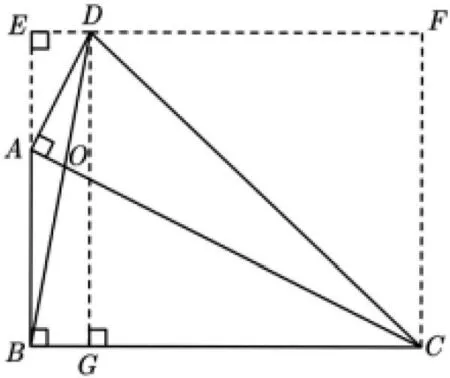
圖10

評注：解法6與解法4、5后續的解答過程類似．

思路6 由圖10，考慮用割補法求三角形的面積．針對ΔABD，比較好算的是采用補形法，即SΔABD=SΔBED-SΔAED．求ΔCBD的面積時，則有如下4種方法．

解法7：SΔCBD=S梯形ΔEBCD-SΔEBD．

解法8：SΔCBD=S梯形ΔEBCD-SΔABD-SΔEAD．

解法9：SΔCBD=SΔBDG+SΔCDG．

解法10：SΔCBD=S矩形EBCF-SΔEBD-SΔDFC．

評注：由解法2易得解法7、8、9、10中所出現的三角形、梯形、矩形的面積，此處不再贅述．

3 變式探究

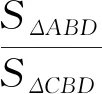
思路1 已知OB與OD的比值和AB與BC的比值，求OA與OC的比值和AD與AC的比值．

變式1 如圖11，已知四邊形ABCD，AC與BD相交于點

求證

變式1的證明由16題的解法1易證出．

思路2 已知OA與OC的比值和AB與BC的比值，去求OB與OD的比值和AD與AC的比值．

變式2 如圖11，已知四邊形ABCD，AC與BD相交于點

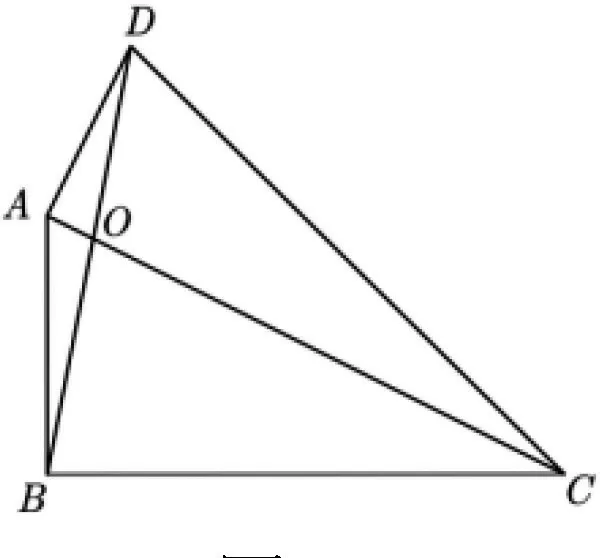
圖11

求證

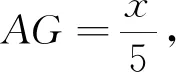
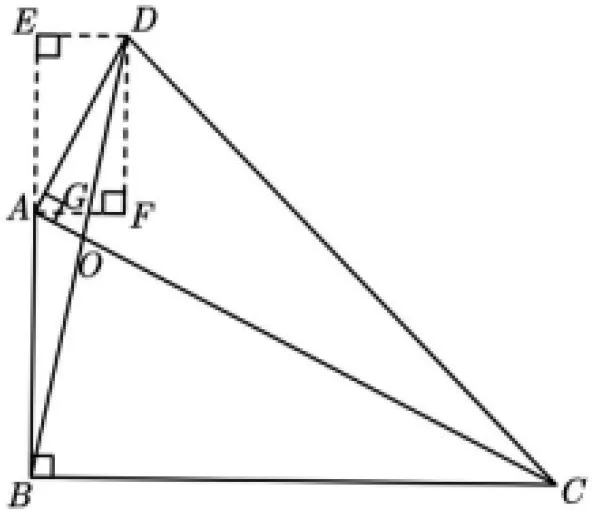
圖12

思路3 已知OB與OD的比值和AD與AC的比值，去求OA與OC的比值和AB與BC的比值．

變式3 如圖13，已知四邊形ABCD，AC與BD相交于點

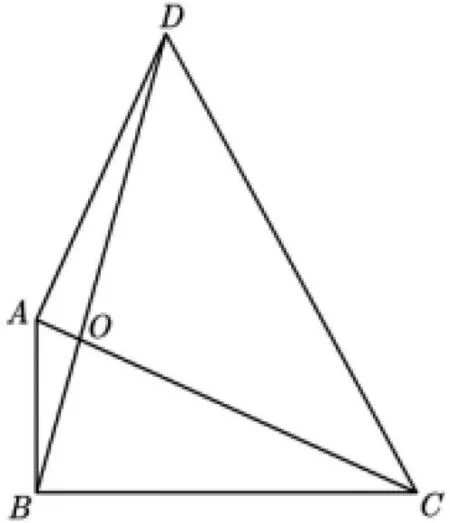
圖13

求證

簡證：如圖14，設AD=3x，則

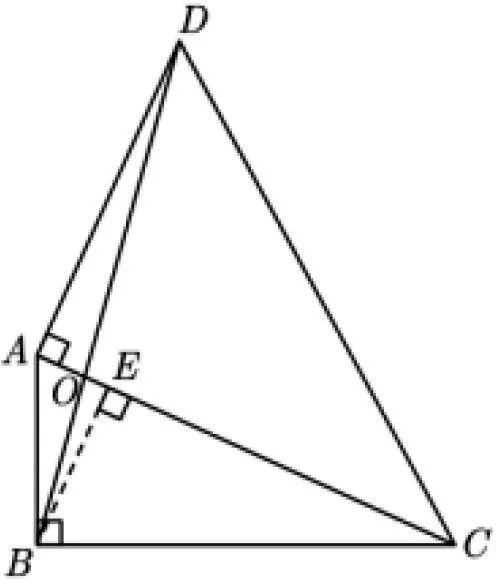
圖14

思路4 已知OA與OC的比值和AD與AC的比值，去求OB與OD的比值和AB與BC的比值．

變式4 如圖15，已知四邊形ABCD，AC與BD相交于點

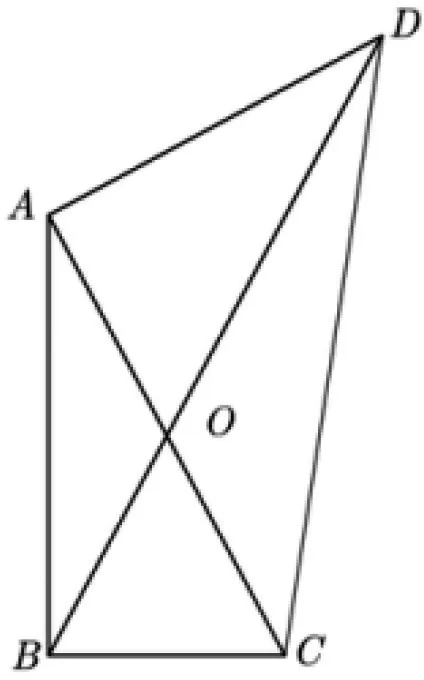
圖15

求證

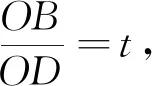
思路5 在背景探究中揭示了本題蘊含的“一線三直角模型”，若圖1中的∠ABC和∠DAC不是直角，結論會怎樣？于是得到如下推廣．

變式5 如圖16，已知四邊形ABCD，AC與BD相交于點

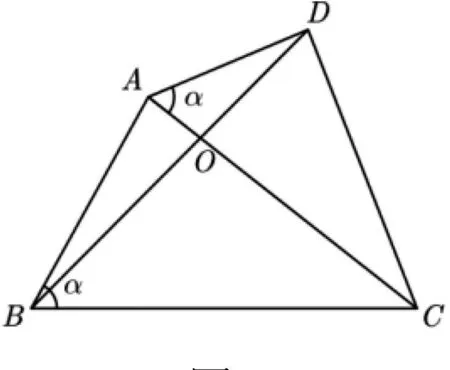
圖16

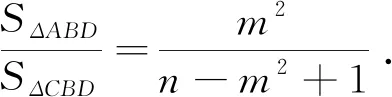
簡證：過點B作AD的平行線與AC相交，方法類似于解法探究中的解法1．

評注：為了描述的簡便性，在RtΔDAC和RtΔABC為載體的四邊形ABCD中，稱OB與OD的比值和OA與OC的比值為“內邊比”、稱AB與BC的比值、AD與AC的比值為“直角三角形的外邊比”．從變式1、2、3、4可知，只要已知任意一組“內邊比”和一組“直角三角形的外邊比”，就可求出另一組“內邊比”和另一組“直角三角形的外邊比”．變式5讓16題更具一般性．