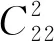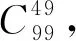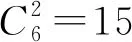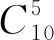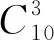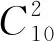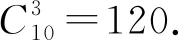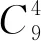一類不定方程整數解問題的求解策略

江蘇省徐州市第一中學 (221004) 許 麗

1．基本問題的求解模型

問題n元一次不定方程x1+x2+…+xn=m(m≥n≥2)的正整數解(x1，x2，…，xn)的組數是多少？

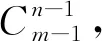
競賽對這一類不定方程問題情有獨鐘，常考常新．梳理近些年各省的預賽和全國聯賽中有關n元一次不定方程的考題，發現這類問題在方程形式和解的制約關系等方面不斷進行變化，通過改變方程的形式、增加限制條件、包裝成別樣面目等，將這類問題演繹得絢麗多姿，精彩紛呈．

2．形態多樣的不定方程

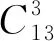
例2 (2009湖北預賽)求不定方程x1+x2+x3+3x4+3x5+5x6=21的正整數解的組數．

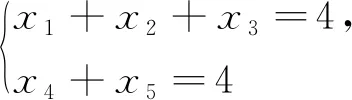
例3 (2021福建預賽)設整數a，b，c滿足0≤a≤10，0≤b≤10，0≤c≤10，10≤a+b+c≤20，則滿足條件的有序數組(a，b，c)共有組．

解析：令a+1=x，b+1=y，c+1=z，則1≤x，y，z≤11，13≤x+y+z≤23．

例4 (2018上海預賽)求不定方程x+y+z+w=25滿足x

例5 (2010全國高中數學聯賽)方程x+y+z=2010滿足x≤y≤z的正整數解(x，y，z)的個數是．

3．千姿百態的廣泛應用

例6 (2002全國高中數學聯賽)已知兩個實數集合A={a1，a2，…，a100}與B={b1，b2，…，b50}，若從A到B的映射f使得B中每個元素都有原象，且f(a1)≤f(a2)≤…≤f(a100)，則這樣的映射共有( ).

例7 (2012黑龍江預賽)將10個相同的小球裝入編號為1，2，3的三個盒子(每次要把十個球裝完)中，要求每個盒子里球的個數不少于盒子的編號數，則這樣的裝法種數為．

例8(2013遼寧預賽)將11個完全一樣的小球放入6個不相同的盒子中，使得至多有3個空盒子的方法種數為．

例9 (2011內蒙古預賽)各位數字之和等于11的四位數的個數為．

例10 (2020浙江預賽)已知由6個正整數組成的六位十進制數中，其個位上的數字是4的倍數，十位和百位上的數字都是3的倍數，且六位數的數碼和為21，則滿足上述條件的六位數的個數為．

解析：由題意知，該六位數后三位(百位、十位、個位)上的數字所有可能為：334，364，394，634，664，934，338，368，638．

例11 (2021上海預賽)在正整數1，2，…，20210418中，有多少個數的數碼和為8？

解析：設這樣的正整數為n．

例12 (2016河北預賽)如果從數1，2，3，…，14中按由小到大的順序取出a1，a2，a3，使得同時滿足a2-a1≥3，a3-a2≥3，那么符合要求的不同取法數為．

例13 (2018湖北預賽)一枚骰子連續投擲4次，從第二次起每次出現的點數都不小于前一次出現的點數的概率為．

例14 (2022重慶預賽)將一枚骰子連續投擲五次，則事件“五次出現的點數既不全相同，也不兩兩互異，且從第二次起每一次的點數都不小于前一次的點數”的概率為．