一道導數聯考題的命制創新與解法分析*

湖北省恩施州教育科學研究院 (445000) 周 威

湖南省長沙市雷鋒學校 (410217) 童繼稀

一、命題靈感與創新

2022屆湖北省七市(州)3月聯考，備受學校和社會關注，命題質量要求較高，而其經典壓軸的導數綜合題，自然成為關注焦點.結合近幾年的高考考查趨勢，此次聯考導數綜合題的多維雙向細目表設置如下：

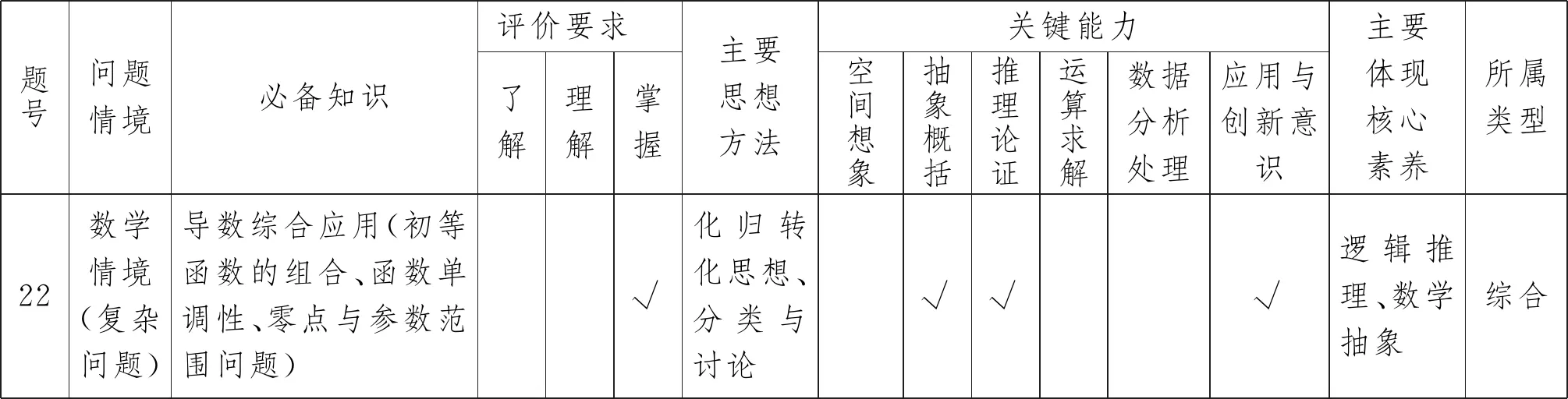
表1 導數綜合題雙向細目表

那么，如何根據表中必備知識、關鍵能力要求命好這道導數綜合題呢？這肯定少不了高考導向與靈感創新．

1．高考導向下的命題靈感

首先，根據必備知識要求，從2021年新高考Ⅰ卷導數題中尋找靈感．

例1 (2021年新高考Ⅰ卷22題)已知函數f(x)=x(1-lnx)．

(1)討論f(x)的單調性；

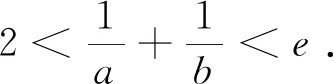
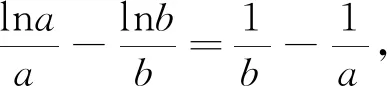
其次，注意到2021年新高考Ⅱ卷導數題綜合考查了含雙參數的關于零點個數問題，試題呈現如下：

例2 (2021年新高考Ⅱ卷22題)已知函數f(x)=(x-1)ex-ax2+b．

(1)討論f(x)的單調性；

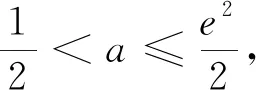
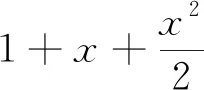
思考到這里，雙向細目表中的“初等函數的組合、零點與參數范圍問題”要求，就有了命題靈感，那就是y=xlnx與二次函數的組合成一個新函數g(x)=xlnx-ax2+b+cx．

接下來的問題是考查一個參數還是兩個參數問題，以及如何確定參數a,b,c的值？考慮到文[2]中對含雙參數函數的零點分類討論的復雜性，還是選擇單參數.另外，注意到對g(x)求導后有g′(x)=lnx+1-2ax+c，設置c=-1方便進一步計算．同時，設置b=1，此時g(1)=-a恰好只含有參數部分．因此，新函數確定為g(x)=xlnx-ax2-x+1，從而設置試題命制初稿如下：

例3 已知函數g(x)=xlnx-ax2-x+1．

(1)當a=0時，討論函數g(x)的單調性；

(2)試討論函數g(x)的零點個數．

2．基于“解決問題能力”的命題創新

在對例3第(2)問的計算過程中發現，

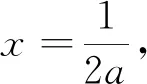
若

若

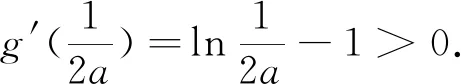
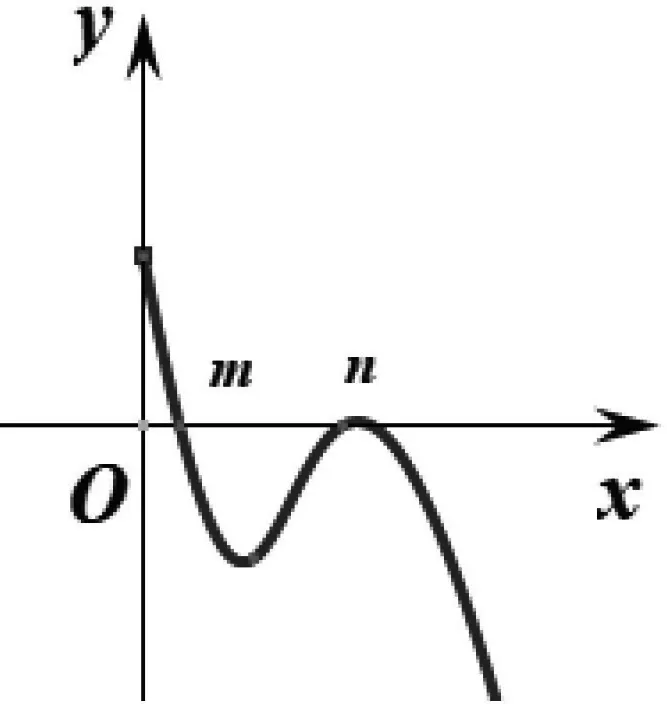
如圖1所示，g(x)在(0,m)上單調遞減，在(m,n)上單調遞增，在(n,+∞)上單調遞減．

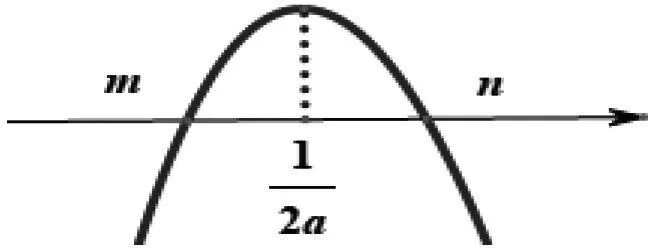
圖1

由g(m)=mlnm-am2-m+1=am2-m+1<0，可知g(n)=nlnn-an2-n+1有三種情況，如圖2所示，且g(n)=0時n為“隱零點”，n的值求不出來，這為后面的討論帶來了困難，因此這就需要對題目進行再修改.

g(n)=0

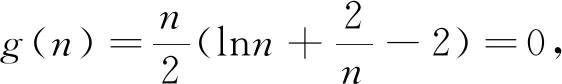
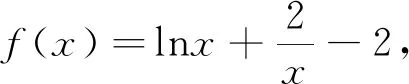
(1)證明：函數f(x)在(1，+∞)上有且僅有一個零點；

(2)假設常數λ>1，且滿足f(λ)=0，試討論函數g(x)的零點個數．

二、試題解法分析

例4第(1)問的證明較為簡單，分值設置為3分，具體證明過程如下：

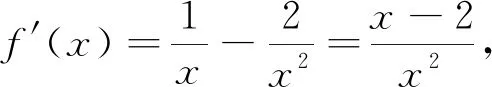
結合單調性得f(x)在(1，+∞)有且僅有一個零點．

例4第(2)問可以從分類討論角度進行求解，也可以從半分離參數或分離參數的角度進行求解，思路入口寬，即實現了導數綜合題兩種常用方法的考查，考查了學生在具體實踐中的問題解決能力.

解法1：(分類討論)由題意

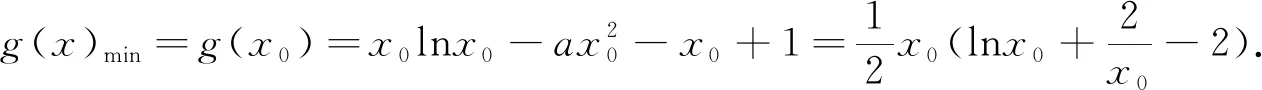
當a=0時，g(x)=xlnx-x+1，g′(x)=lnx．令g′(x)=0，解得x=1，則g(x)在(0,1)上單調遞減，在(1,+∞)上單調遞增，g(x)min=g(1)=0，可得g(x)只有一個零點．

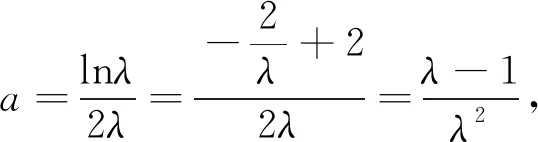
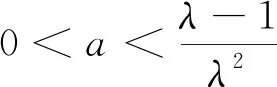
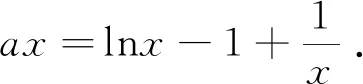
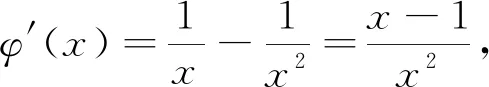
當a=0時，y=ax圖像與φ(x)圖像有一個交點；

當a<0時，y=ax圖像經過二、四象限，與φ(x)圖像無交點；

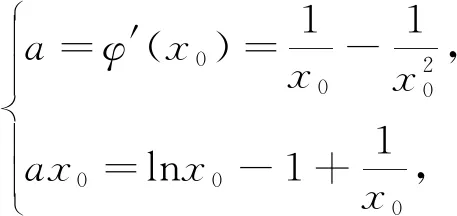
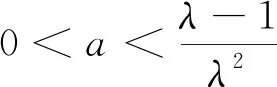
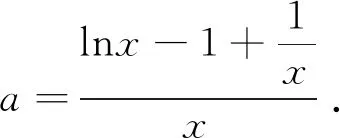
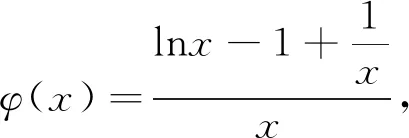
結合(1)可知，φ(x)在(0,1)上單調遞減，0在(1,λ)上單調遞增，在(λ,+∞)上單調遞減，如圖3所示．又

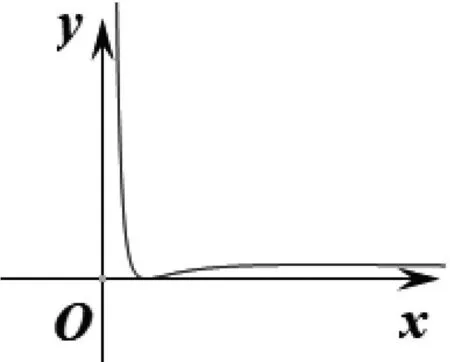
圖3

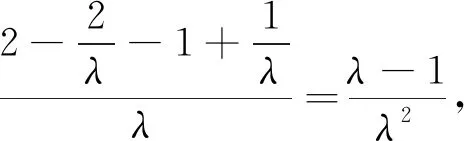
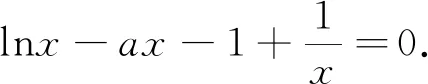
令函數φ(x)=ax2-x+1,x∈(0,+∞)．

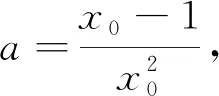
同(1)問，可證函數f(x)在x∈(0,1)單調遞減，則h(x)min=f(x0)>f(1)=0，可得函數h(x)在(0,+∞)無零點．

當a=0時，可得x∈(0,1)時，φ(x)>0，即h′(x)<0，則函數h(x)單調遞減；x∈(1,+∞)時，φ(x)<0，即h′(x)>0，則函數h(x)單調遞增，有h(x)min=h(1)=0，故h(x)在(0,+∞)只有一個零點．

當a>0時，根據判別式Δ=1-4a的符號分情況討論．

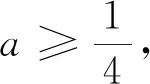
可得函數h(x)在(0,+∞)只有一個零點．

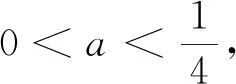
則函數h(x)在(0,1)有一個零點；而在(1,+∞)的零點個數由極大值h(x2)的符號決定，函數h(x)圖象有圖4的3種情況如下：

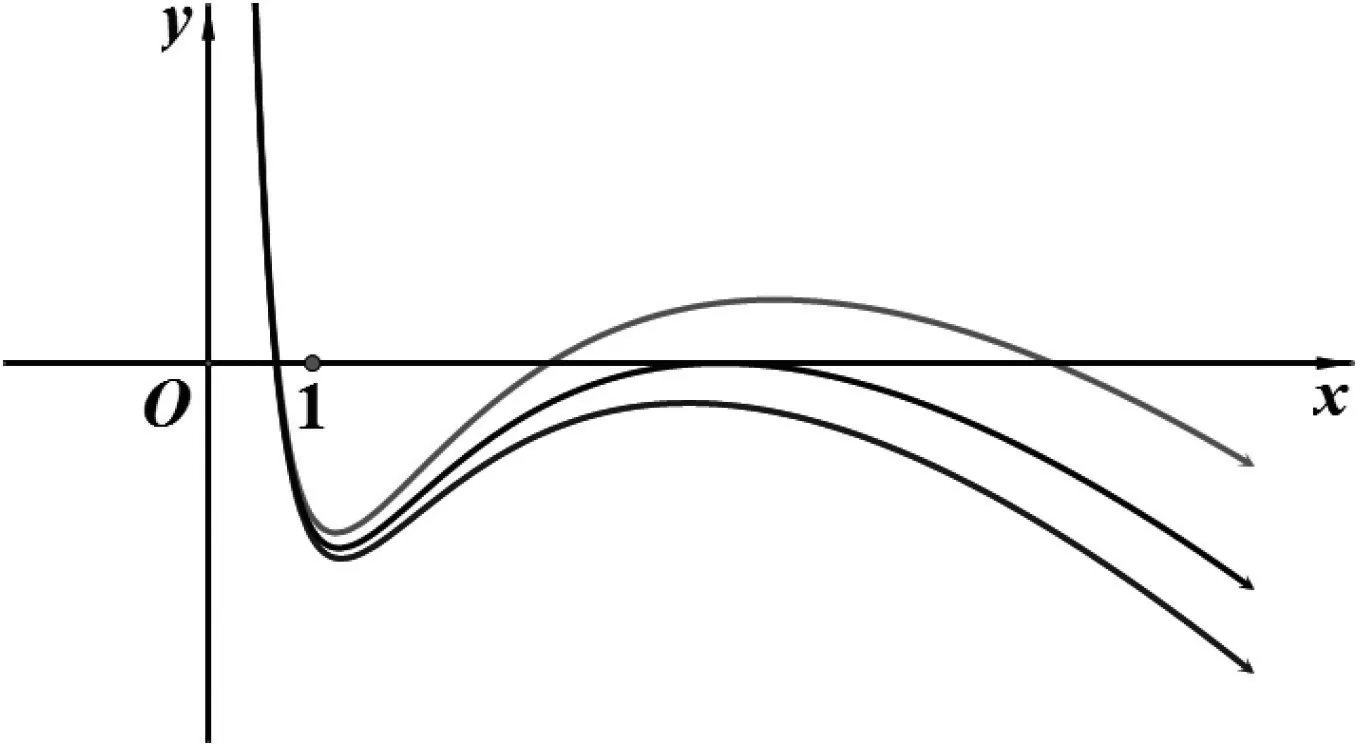
圖4

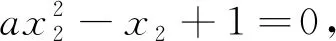
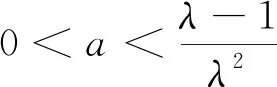
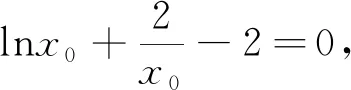
三、考試結果評價與結語

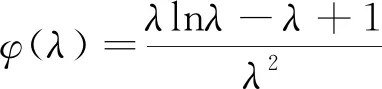
結合上述命題意圖和考試結果分析，在二輪復習教學中，依然要注重基礎知識和基本解題技能的滲透，對優秀學生的計算能力、轉化化歸能力、直觀想象能力進行專項突破，對函數導數板塊知識做好分層教學，因材施教，使得不同思維水平的學生的得分均得到體現．