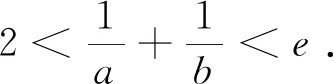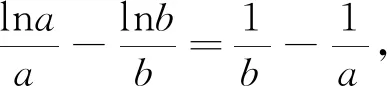一道高考導數壓軸題的解法探究

廣東省中山市濠頭中學 (528437) 李 方 楊沛娟

一、試題呈現及分析

分析：(1) 首先確定函數的定義域，然后求得導函數的解析式，求出函數的導數，由導函數的符號即可確定原函數的單調性.

二、試題解答

第(1)小題解法如下：f(x)的定義域為(0,+∞)．由f(x)=x(1-lnx)得f′(x)=-lnx，當x=1時，f′(x)=0；當x∈(0,1)時f′(x)>0；當x∈(1,+∞)時，f′(x)<0．故f(x)在區間(0,1]內為增函數，在區間[1,+∞)內為減函數.

本文主要分析第(2)小題的解法.

先證x1+x2>2.若x2≥2，x1+x2>2必成立.若x2<2， 要證x1+x2>2，即證x1>2-x2，而0<2-x2<1，故即證f(x1)>f(2-x2)，即證f(x2)>f(2-x2)，其中10，所以g′(x)>0，故g(x)在(1,2)為增函數，所以g(x)>g(1)=0，故f(x)>f(2-x)，即f(x2)>f(2-x2)成立，所以x1+x2>2成立.綜上，x1+x2>2成立.

設x2=tx1，則t>1，結合

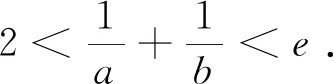
評注：極值點偏移問題，一般利用通過原函數的單調性，把與自變量有關的不等式問題轉化與原函數的函數值有關的不等式問題，也可以引入第三個變量，把不等式的問題轉化為與新引入變量有關的不等式問題.

[2]雍照章.開發中職專業技能課程標準的基本問題分析 [J].職業技術教育,2017,38(10):24-29.

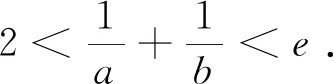
評注：等價轉化是處理導數問題的常見方法，其中利用的對稱差函數，構造函數的思想，這些都是導數問題必備的知識和技能.

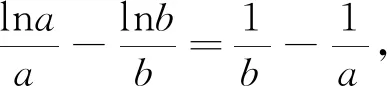
令f(x)=x(1-lnx)，則f(m)=f(n)，不妨設m2．要證m+n>2?n>2-m?f(n)2．

再證m+nm，所以需證n(1-lnn)+n0，故h(x)在(1,e)內單調遞增．所以h(x)

評注：等價轉化是常見的數學思想，構造對稱差函數是最基本的極值點偏移問題的處理策略.

點評：解法4用到了比值代換，這是一種將雙變量問題化為單變量問題的有效途徑，然后構造函數利用函數的單調性證明題中的不等式即可.

評注：解法5用到的是構造函數法，構造函數之后想辦法出現關于x1+x2-e<0的式子，這是本方法證明不等式的關鍵思想所在.