帶紅利和交易成本的歐式期權三叉樹定價

茹琴

摘要：文章考慮按已知紅利率和交易成本比例以及按固定紅利額和交易成本額支付一次紅利和交易成本，分別推導出含紅利和交易成本的三叉樹模型，通過矩陣算法計算該模型下期權的理論價格，并選取2020年9月25日至2020年12月23日上證50ETF三份認購期權合約的交易數據，對上述模型進行檢驗，結果表明，考慮紅利率和交易成本比例的三叉樹模型能夠較好地反映市場的真實情況，且精確度高于考慮固定紅利額和交易成本額的三叉樹模型和不含紅利和交易成本的三叉樹模型。

關鍵詞：歐式期權；三叉樹；紅利；交易成本

一、引言

近年來，我國金融市場發展迅速，市場規模不斷壯大，投資者對金融衍生產品的需求日益強烈。期權作為一種金融衍生產品，自1973年期權定價公式出現以來，日漸成為交易者投資決策時獲取利益信心的產品之一，在增強金融市場的穩定性和流動性等方面都具有重要意義，因此期權定價是否合理顯得至關重要。隨著金融市場的迅速發展，期權的定價模型也在不斷地更新與修正，目前已有很多發展比較成熟的期權定價模型，二叉樹模型就是其中之一。該模型最早是在1979年由Cox等提出，此后因應用簡單高效得到了快速發展，隨之而來的問題是該模型在實際應用中存在模型誤差。為了解決二叉樹定價方法的精確度問題，1986年，Boyle P P在二叉樹模型的基礎上進行拓展，提出了三叉樹模型，隨后Ahn等證明了三叉樹定價模型的收斂效果以及精確性。目前有關二叉樹和三叉樹期權定價模型的研究很少有考慮支付紅利和交易費用的情況，具體來說，張鐵借助隨機誤差校正的方法構造出了精確度較高的新型二叉樹參數模型。韓立杰等利用矩的思想構造出了B-S定價公式Δt上一階近似的新型三叉樹模型定價公式。宮文秀等給出了復合期權三叉樹模型，并結合實例分析了相關影響變量的敏感度。李昊軒等借助隨機方程和原點矩思想，在二叉樹模型的基礎上，給出了三叉樹模型參數和期權價格的遞推表達，證明了三叉樹模型的收斂性和穩定性更好。然而，實際的金融市場中，股票交易需要支付紅利和交易成本，因此在期權的定價模型中需要融入交易成本和紅利以適應金融市場的實際情況。任芳玲等基于經典的B-S-M模型，考慮交易費用，并利用模型的解析式法，二叉樹定價方法以及三叉樹定價方法計算期權價格。宮文秀等在傳統的三叉樹定價方法基礎上，引入CARCH模型，給出了隨機市場模型下支付固定比例紅利和交易費用的歐式看漲期權的三叉樹模型。

現有文獻中，將交易成本和紅利融入三叉樹期權定價模型中的研究較少。因此，本文考慮支付一次紅利和交易成本，推導出含有交易成本和紅利的歐式期權的三叉樹模型，使該定價方法更符合金融市場的實際情況，并借助矩陣算法計算期權價格，最后通過選取上證50ETF三份認購期權的實際交易數據，對文中模型進行分析和檢驗。

二、模型說明

（一）三叉樹模型

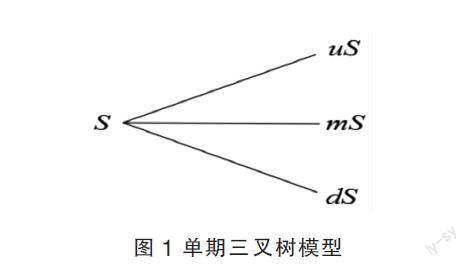
三叉樹模型是在二叉樹模型基礎上的擴展延伸，與二叉樹模型的定義類似，不同于二叉樹模型的是，在期權有效期的每個時間段的節點上，期權價格的變化有三種可能：上升、持平和下降。如圖1所示，標的資產在交易過程中有不確定的三種變化值uS、mS以及dS。

其中，u，m，d滿足d<m=1<u。假設股票價格上升的概率為pu，下降的概率為pd，保持不變的概率為pm，且概率測度需滿足：

pu+pm+pd=1

將期權的有效期[0，T]分為N個長度為Δt（Δt＝T/N）的相等時間段，股票的初始價格為S0，i為第i（1≤i≤N）個時刻，j表示對應時刻第j（1≤j≤2i-1）個支點，則在結點（i，j）處的股票價格為：

Si，j＝S0ui-1dj-1

其中，1≤i≤N，1≤j≤2i-1。在不考慮支付紅利和交易成本時，令歐式期權的到期日為，到期日執行價格為K，fi，j為iΔt時刻在結點（i，j）的期權價格，則歐式看漲期權的價格為：

fN，j＝max（0，S0uN-1dj-1-K），0≤j≤2N-1

在風險中性概率測度p下，可得到在任意結點（i，j）的風險中性定價公式：

fi，j=e-rΔt[pufi+1，j+pmfi+1，j+1+pdfi+1，j+2]

上述兩式中的參數滿足：

pu=■，

pm=■

pd=■，

u=M+■，d=M-■

其中，r為無風險收益率，σ為標的資產波動率，M＝■。

（二）已知紅利率和交易成本比例的三叉樹模型

期權在實際的金融市場交易中，往往會支付紅利和交易費用，支付紅利會引起股票價格下降，支付交易費用會引起股票價格上升，股票價格下降和上升的幅度分別為每股股票支付紅利和交易費用的金額，依據金融市場交易規律，由紅利引起的股票價格下跌的幅度往往要高于由交易費用引起的股票價格上漲的幅度。假設有效期內期權僅支付一次紅利和交易成本，紅利率為δ，交易成本收取比例為k，在除息日這一時刻結點，按照上述方法可以得到：

除息日之前結點（i，j）的股票價格為：

Si，j＝S0ui-1dj-1

除息日之后結點（i，j）的股票價格為：

Si，j＝S0（1-δ+k）ui-1dj-1

如果有效期內期權支付多次紅利，且除息日在結點（i，j）之前，令δi為時刻i之前所有除息日支付紅利的紅利率總和，結點（i，j）相對應的股票價格為：

Si，j＝S0（1-δi+k）ui-1dj-1

對上述模型使用矩陣算法進行計算，考慮僅支付一次紅利和交易成本，紅利率為δ，固定交易成本比例為k，則參照文獻可以得出如下定理：

定理1：到期日之前按照已知的紅利率δ和固定交易比例k支付一次紅利和交易成本，則歐式期權價格在時刻tN有2N-1種可能，分別為：

fN，1，fN，2，…，fN，2N-1

令行矩陣F＝（fN，1，fN，2，…，fN，2N-1），G為2N-1階矩陣，設

G＝p■? 0? … 0 0 0p■ p■ … 0 0 0p■ p■ … 0 0 00? p■ … 0 0 0┆┆？塤 ┆┆┆0? 0 … p■ 0 00? 0 … p■ 0 00? 0 … p■ 0 0

則T1時刻期權的價格為：f=e-rNΔtFG■■，其中G■■為G的N次冪的第一列。

證明 由三叉樹方法可知TN-1時刻各結點的期權價格：

結點（N-1，1）的期權價格為：

fN-1，1＝e-rΔt[pufN，1+pmfN，2+pdfN，3]=e-rΔt（fN，1，fN，2，fN，，3，fN，4，…，fN，2N-1）（pu，pm，pd，0，…，0）T

結點（N-1，2）的期權價格為：

fN-1，2＝e-rΔt[pufN，2+pmfN，3+pdfN，4]=e-rΔt（fN，1，fN，2，fN，，3，fN，4，…，fN，2N-1）（0，pu，pm，pd，0）T

以此類推，結點（N-1，2N-3）的期權價格為：

fN-1，2N－3＝e-rΔt[pufN，2N-3+pmfN，2N+pdfN，2N-1]

=e-rΔt（fN，1，fN，2，fN，，3，fN，4，…，fN，2N-1）（0，…，0，pu，pm，pd）T

綜合可得，

（fN-1，1，fN-1，2，…，fN-1，2N－3，0，0）＝e-rΔtFG1

繼續按照結點（N-1，1）的方法推導出結點TN-2時刻各節點的期權價格。

結點（N-2，1）的期權價格為：

fN-2，1＝e-rΔt[pufN-1，1+pmfN-1，2+pdfN-1，3]=e-rΔt（fN-1，1，fN-1，2，fN-1，3，fN-1，4，…，fN，2N－3，0，0）（pu，pm，pd，0，…，0）T

結合TN-1時刻各節點的期權價格可得

fN-2，1＝e-2rΔtFG1（pu，pm，pd，0，…，0）T

同理可得：

fN-2，2N－5＝e-2rΔtFG1（0，…，0，pu，pm，pd）T

整理得：

（fN-2，1，fN-2，2，…，fN-2，2N-5，*，*，0，0）＝e-2rΔtFG2

TN-2時刻共有2N-5個節點，因此只需考慮（fN-2，1，fN-2，2，…，fN-2，2N-5），*表示的內容不在本文考慮范圍內，故沒有展示具體內容。繼續向前推導每個時刻各節點的期權價格，最終可以得到T1時刻節點（1，1）的期權價格為：

（f1，1，*，…，*，0，0）＝e-NrΔtFGN

*表示的內容不在研究范圍內，因此，可以得到T1時刻期權的價格為：

f＝e-NrΔtFG1N

其中，G1N為G的N次冪的第一列。則歐式看漲期權定價公式為：

fN，j＝max（S0（1-δ+k）uN-1dj-1-K，0）

其中，fN，j可由定理1中行矩陣F的各元素確定。如果期權在有效期內多次支付紅利，可按上述算法進行計算，即將一次支付紅利率δ替換為多次支付紅利率總和δi即可。

（三）已知紅利額和交易成本額的三叉樹模型

假設期權在有效期內按已知的數額支付紅利和交易成本，則三叉樹圖在支付紅利和交易成本后的樹枝不再重合，若考慮支付多次紅利，需考慮的結點數過多，過程較為繁瑣，因此本文僅考慮支付一次紅利和交易成本。令股票的波動率σ為常數，除息日τ在時刻lΔt和（l+1）Δt之間，支付紅利數額為D，支付交易成本數額為H，這時任意結點（i，j）處期權的價值需要從以下幾點來考慮。

1.當i≤l時，此時未到除息日τ，因此不需要考慮支付紅利和交易成本，任意結點相對應的股票價格為：

Si，j＝S0ui-1dj-1，1≤j≤2i-1

2.當i=l+1時，此時已在除息日支付紅利和交易成本，任意結點相對應的股票價格為：

Si，j＝S0ui-1dj-1-D+H，1≤j≤2i-1

3.當i=l+2時，此時任意結點對應的股票價格應基于支付紅利和交易成本后的股票價格來計算，股票價格為：

u（S0ui-1dj-1-D+H），S0ui-1dj-1-D+H和d（S0ui-1dj-1-D+H）

其中1≤j≤2i-1，此時，三叉樹將有3（i+1）個結點而不是2i-1個結點。則在（l+m）Δt時刻，將有（2m-1）（2l-1）個結點而不是2（l+m）-1個結點。由于支付紅利和交易成本后，樹枝不再重合，為解決這一問題，可將股票價格考慮為由兩部分組成，一部分考慮為不確定的股票價格，另一部分考慮為有效期內期權支付紅利和交易成本決定的股票價格。令不確定的股票價格為S*，此時股票價格的波動率σ*為常數，在期權的有效期內有個除息日τ，且lΔt≤τ≤（l+1）Δt，則在任意時刻iΔt時刻，不確定的股票價格S*為：

S*=S，iΔt＞τS*＝S-（D-H）e-r（τ-iΔt），iΔt≤τ

通過這種方法可以將支付的紅利和交易成本加在每個節點的股票價格上，這樣就可以恢復原來三叉樹的重合狀態，iΔt時刻恢復2i-1個結點。此時，在iΔt時刻，任意結點所對應的股票價格可由下面的公式給出。

當時刻iΔt在除息日τ當日或之前，即iΔt≤τ，任意結點股票價格為：

S*ui-1dj-1+（D-H）e-r（τ-iΔt），j=1，2，…，2i-1

當時刻iΔt在除息日τ之后，即iΔt＞τ，任意結點股票價格為：

S*ui-1dj-1，j=1，2，…，2i-1

定理2：按已知數額D和H支付一次紅利和交易成本，則歐式期權價格在tN時刻的2N-1種可能，分別為：

fN，1，fN，2，…，fN，2N-1

行矩陣F和2N-1階下三角矩陣G與定理1一致，則在T1時刻期權的價格為：

f=e-NrΔtFG■■

其中，G■■為下三角矩陣G的N次冪的第一列。該定理的證明過程和定理1一致，在此不作重復證明。在到期日T，歐式看漲期權的定價公式為：

fN+1，j＝max（■-K，0），j=1，2，…，2N-1；

其中，■的定義和上文一致，由不確定的股票價格S*確定，公式如下：

■＝S*ui-1dj-1+（D-H）e-r（τ-iΔt），iΔt≤τS*ui-1dj-1，iΔt＞τ。

三、實證分析

（一）變量選取及數據說明

本文采用上證50ETF期權的實際交易數據對上述模型進行實證分析，選擇樣本區間為期權持有期是2020年9月25日至2020年12月23日的三份認購期權合約，分別為50ETF購12月3844A、50ETF購12月3746A以及50ETF購12月3647A，數據均來源于東方財富Choice金融終端。根據上述模型可知，期權價格主要受標的資產價格S，期權執行價格K，到期日T，無風險利率r，標的資產波動率σ，紅利以及交易成本的影響。

1.標的資產價格S。本文選取樣本區間內三份認購期權所對應的標的資產在交易日的收盤價作為標的資產價格S，選取三份認購期權每日的收盤價作為期權的實際市場價格。例如，2020年10月15日標的資產收盤價為3.4250元，則S＝3.4250。

2.期權執行價格K。三份認購期權的執行價格分別為3.8440，3.7460以及3.6740。

3.到期日T。本文選取的樣本區間共58個交易日，上證50ETF期權一年大約有250天交易日，令Δt為期權上市的交易天數，則到期日為：

T＝■

4.無風險利率r。本文選取和期權樣本同期的上海銀行間同業拆放利率6個月期shibor利率的平均值作為無風險利率r，經過計算，無風險利率r的年化利率為2.9%。

5.標的資產波動率σ。本文的標的資產波動率采用歷史波動率，即選取樣本區間第一天之前的58天的數據來計算標的資產波動率，計算公式如下：

σ＝■×■

其中，μi=ln（Si/Si-1），i=1，2，…，n，n＝58。根據公式計算出標的資產的歷史波動率約為0.222。

6.紅利。樣本區間內紅利的除息日為2020年11月30日，每份分紅為0.051元。紅利率為紅利和標的資產價格的比值，標的資產價格本文選取除息日標的資產的收盤價格，計算出紅利率為1.5%。

7.交易成本。本文選取上證50ETF期權的基金運作費用率0.6%作為交易成本比例，選取樣本區間內標的資產的均值和基金運作費用率的乘積作為交易費用，計算結果為0.021。

（二）上證50ETF期權理論價格

根據對各參數的介紹，分別計算出所取樣本含紅利和交易費以及不含紅利和交易費的期權價格，并與實際的市場價格進行比較，三份認購期權的理論價格與實際價格比較折線圖如圖2和圖3所示，BC表示含有紅利和交易成本的期權理論價格，NBC表示不含紅利和交易成本的期權理論價格，從中可以看出，無論是已知紅利率和交易成本比例，還是已知紅利額和交易成本額，三份認購期權考慮紅利和交易費用的理論價格以及不考慮紅利和交易費用的理論價格均能較好地貼近實際價格，且價格的變化趨勢基本一致，也可以清晰地看出，考慮已知紅利率和交易成本比例的三叉樹期權定價模型可以貼近上證50ETF期權的實際價格，說明在實際的金融市場中，紅利和交易費用會影響期權的定價。

（三）誤差分析

除了折線圖直觀的描述之外，還可以通過誤差分析來說明含紅利和交易費用期權定價模型的效率。本文主要選取以下三種誤差來進行分析，假設期權的實際價格為Pactual，期權的理論價格為Ptheory，樣本量為，則可以得到以下誤差分析公式：

1.平均絕對誤差（MAE）

MAE=■■｜P■-P■｜

2.平方絕對百分比誤差（MAPE）

MAPE=■■｜■｜×100%

3.均方根誤差（RMSE）

RMSE=■

根據上述三個誤差公式，對含紅利和交易費用的期權定價模型以及不含紅利和交易費用的期權定價模型計算出的理論價格分別進行誤差分析，結果如表1所示。

MAE，MAPE以及RMSE主要衡量的是期權的實際價格與理論價格之間偏差的大小，值越小說明模型的精確度更高。從表1中可以看出，三份認購期權考慮紅利率和交易成本比例的理論價格的誤差均小于不含紅利和交易成本的理論價格的誤差，說明在對上證50ETF進行定價時，考慮紅利率和交易成本比例的定價模型精確度更高。也同樣可以看出考慮紅利額和交易成本額的定價模型的精確度要低于考慮紅利率和交易成本比例的定價模型。

四、結語

本文在傳統三叉樹期權定價方法的基礎上，考慮支付一次分紅和交易成本，推導出含有紅利和交易成本的歐式期權的三叉樹定價方法，再結合矩陣算法，得到了歐式期權價格基于三叉樹期權定價模型的數值求解方法。最后，本文選取2020年9月25日至2020年12月23日上證50ETF三份認購期權合約的交易數據，對其進行實證分析，結果表明，考慮紅利率和交易成本比例的三叉樹定價方法可以較好地貼近期權的實際市場價格，更符合市場的真實情況，考慮紅利額和交易成本額的三叉樹定價方法相對來說貼合度較弱，三種誤差MAE，MAPE以及RMSE也進一步表明考慮紅利率和交易成本比例的三叉樹定價方法的精確度優于不含紅利和交易成本的三叉樹定價方法以及考慮紅利額和交易成本額的三叉樹定價方法。

參考文獻：

[1]COX J C， ROSS S A， RUBINSTEIN M.Option pricing： a simplified approach[J].Journal of Financial Economics，1979，7（03）：229-263．

[2]Boyle P P.Option Valuation Using a Tree-Jump Process[J].International Options Journal，1986，3：7-12．

[3]Ahn J，Song M.Convergence of the Trinomial Tree Method for Pricing European/American Options[J].Applied Mathematics and Compution，2007，189（01）：575-582.

[4]張鐵.一個新型的期權定價二叉樹參數模型[J].系統工程理論與實踐，2000，20（11）：90-93.

[5]韓立杰，劉喜波，劉宇.期權定價的新型三叉樹方法[J].數學的實踐與認識，2007，37（18）：39-42.

[6]宮文秀，高凌云.復合期權的三叉樹模型[J].統計與決策，2016（18）：83-86．

[7]李昊軒，賀鈺淇，張昊陽，解菲.基于Vasicek隨機利率模型的美式期權三叉樹定價[J].中國商論，2020（16）：44-47.

[8]任芳玲，薛盼紅.考慮交易費用和泊松過程的滬深300股指期權定價研究[J].湖北大學學報（自然科學版），2018，40（04）：327-332.

[9]宮文秀，許作良.基于CARCH模型的三叉樹期權定價方法[J].數學的實踐與認識，2020，50（07）：106-114.

[10]覃思乾.基于二叉樹模型期權定價的矩陣形式算法[J].廣西師范學院學報，2006，23（01）：26-30.

（作者單位：湖北工業大學理學院）