多元線性回歸模型在河流水質(zhì)預測中的應用

李秋瑤

摘要：為實現(xiàn)基于水質(zhì)自動監(jiān)測數(shù)據(jù)對未來水質(zhì)數(shù)據(jù)的快速預測預報，以水質(zhì)自動監(jiān)測數(shù)據(jù)為基礎，結合統(tǒng)計學基本原理，基于多元線性回歸模型建模，將前一日自動監(jiān)測數(shù)據(jù)作為自變量，后一日各污染源因子濃度作為因變量，研究建立河流水質(zhì)預測模型的變化響應關系。通過對模型的檢驗和校正，在試驗斷面上，基本達到了快速預測預警的效果，模型在實際預測中效果較好。該方法所需數(shù)據(jù)較少，預測快速，準確及時，因此，該方法可作為輔助手段應用于實際水質(zhì)監(jiān)測預警工作。

關鍵詞：多元線性回歸預測；河流水質(zhì)預測；水質(zhì)預測方法

一、前言

水質(zhì)自動監(jiān)測是一項與國民經(jīng)濟密切相關的基礎工作，也是開展水質(zhì)預測預警的重要前提[1]。科學準確的水質(zhì)預測預警有助于認識水質(zhì)變化的規(guī)律和發(fā)展態(tài)勢，增加其在保障水質(zhì)安全、水污染防治上的決策主動性和工作效率[2-3]。

近年來，《國務院關于印發(fā)水污染防治行動計劃的通知》[4]等一系列通知，明確提出改善水環(huán)境質(zhì)量的目標和要求，旨在推進重點流域污染治理，切實改善水環(huán)境質(zhì)量。對于重點河流斷面，持續(xù)開展水質(zhì)預測，以預測數(shù)據(jù)作為后續(xù)污染防治工作決策的依據(jù)，具有重要的現(xiàn)實意義。

隨著地表水自動監(jiān)測技術的成熟和推廣應用，環(huán)境監(jiān)測監(jiān)管部門能夠?qū)崟r獲取監(jiān)測點位的水質(zhì)情況。自動監(jiān)測數(shù)據(jù)監(jiān)測頻率高，監(jiān)測時間連續(xù)，具備開展大數(shù)據(jù)統(tǒng)計預測的條件。各地也陸續(xù)開展了相關的研究和試點工作，利用自動監(jiān)測數(shù)據(jù)開展統(tǒng)計預測有以下研究意義：①由于自動數(shù)據(jù)實時性高，可基于自動監(jiān)測數(shù)據(jù)實現(xiàn)快速預測預報；②自動監(jiān)測數(shù)據(jù)量大，時序性高，因此可有效提高水質(zhì)預測精度；③通過基于自動監(jiān)測數(shù)據(jù)的水質(zhì)預測能及時感知污染風險；④通過預測值和實測值比較，當相差較大時，說明條件發(fā)生了較大變化，尤其當實測偏大時應排查異常，及時把控風險。

通常，河流水質(zhì)預測采用綜合指標法、平均增長率法等經(jīng)驗類推可以取得較好的研究結果[5]，但需要滿足河流斷面受周邊影響小、水質(zhì)變化小的前提，如河流斷面水質(zhì)受周邊環(huán)境影響較大，其實際數(shù)據(jù)變化不規(guī)則，采用類推的方法則達不到理想的效果，因此需要采用建立模型的方法進行水質(zhì)預測。目前常用定額預測法、回歸分析法、灰色預測法等水質(zhì)預測方法。本研究采用多元線性回歸分析法進行模型建模。多元線性回歸模型不僅要對回歸系數(shù)進行檢驗，還需要對假設性和共線性作用方面進行研究與驗證，從而優(yōu)化變量，篩選適合的模型，增加水質(zhì)預測的精確度。

二、多元線性回歸方法基本原理

（一）多元線性回歸模型

對于河流的水質(zhì)預測，水質(zhì)變化結果通常是多個因素共同影響的結果，因此，由多個自變量篩選優(yōu)化后建立的多元線性回歸模型，比單一自變量建立的一元線性回歸模型更符合實際，更加準確與客觀。目前，常規(guī)的水質(zhì)自動監(jiān)測因子包括：水溫、pH值、溶解氧、電導率、濁度、高錳酸鹽指數(shù)、氨氮、總磷、總氮等。以溶解氧為例，假定河流水質(zhì)濃度與前一日各因子濃度間存在線性關系如下：

y=a₀+a₁x₁+a₂x₂+a₃x₃+…a_nx_m+ε

式中，y為因變量，x₁，x₂，x₃，……，x_m為自變量，a₁，a₂，……，a_n為回歸系數(shù)；ε為隨機誤差，假定ε～N（μ，σ²）。

（二）數(shù)據(jù)來源

本研究根據(jù)前一日各監(jiān)測因子的濃度水平來判定對當日監(jiān)測因子的影響，以溶解氧因子為例，選擇溶解氧作為預測因子是因為溶解氧是研究地表水自凈能力的一種重要依據(jù)，相對其他因子來說，溶解氧與水溫、pH及其他因子有著密切的關系，因此可以假定溶解氧濃度可通過前一日各項因子濃度進行預測。

本研究建模數(shù)據(jù)來源于2022年1月至6月廣西某湖庫水質(zhì)自動站的監(jiān)測數(shù)據(jù)日均值。該水站小時數(shù)據(jù)有效率為97.32%，日數(shù)據(jù)有效率大于99%。其有效自動監(jiān)測數(shù)據(jù)的完整度和連續(xù)性為研究數(shù)據(jù)演變關系提供了很大便利，水站監(jiān)測數(shù)據(jù)包括水溫、pH值、溶解氧、電導率、濁度、高錳酸鹽指數(shù)、氨氮、總磷、總氮。設自變量前一日水溫為x₁，pH為x₂，溶解氧為x₃，電導率為x₄，濁度為x₅，高錳酸鹽指數(shù)為x₆，氨氮為x₇，總磷為x₈，總氮為x₉，因變量溶解氧預測濃度為y。

三、建立方程模型

本文采用的模型基于R語言編寫。首先，將訓練數(shù)據(jù)輸入R語言，通過線性回歸模型進行建模，第一次建模得到模型擬合數(shù)據(jù)與實際數(shù)據(jù)的R²為0.9596，R²度量了多元線性回歸模型的擬合優(yōu)度，說明擬合優(yōu)度較好，但模型反應水溫、高錳酸鹽指數(shù)、總磷、總氮P值較大，P值代表犯第一類錯誤（Ⅰ型錯誤）的概率，在回歸方程中，體現(xiàn)了自變量的顯著性。P值越大，說明自變量顯著性越低。從第一次模型參數(shù)中得出，水溫、高錳酸鹽指數(shù)、總磷、總氮的顯著性較低，因此將4個指標剔除后重新建模，R²為0.9594，且整體顯著性與第一次建模相當，且剔除指標后由于減少了干擾，剩余指標的顯著性得到了提升。可推斷出因變量yi可以被前一日pH、溶解氧、電導率、濁度、氨氮濃度的線性方程進行描述，即：自變量為{x₂，x₃，x₄，x₅，x₇}。

通過重新建模，用上一日水質(zhì)因子數(shù)據(jù)與當日水質(zhì)因子數(shù)據(jù)，建立多元線性回歸方程為：

y=4.943388-0.284600x₂+0.913373x₃-0.009313x₄+0.020536x_₅-0.602887x₇

四、模型檢驗

（一）模型優(yōu)化

回歸模型的優(yōu)化主要從模型假設診斷，多重共線性進行模型的優(yōu)化，首先需要診斷多元回歸模型和假設相符，即模型的殘差呈正態(tài)分布。其次，模型的自變量不存在多余重復信息，為簡化模型提供依據(jù)。

1.模型診斷

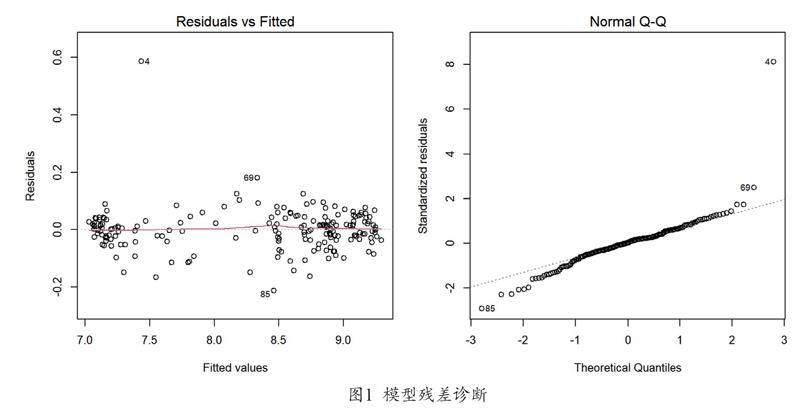
通過繪制殘差圖診斷模型的假定，從圖1殘差圖中可以看出，第4點、第69點、第85點有較大殘差，其中第4點的殘差較大。據(jù)調(diào)查是該日藻類增加導致pH、溶解氧同時增加，pH前三日數(shù)據(jù)分別為7.16、7.14、7.23，第4日突增到8.02，溶解氧前三日數(shù)據(jù)分別為6.89、6.39、6.82，第4日突增到7.45，但都在3類標準范圍內(nèi)，因此驗證了該模型方法對突發(fā)事件預警的能力。排除4號點影響后，模型整體殘差在兩側(cè)分布均勻，在-0.2與0.2之間，殘差期望值接近于0。通過圖1模型的正態(tài)Q-Q圖檢驗，對應點分布在y=x附近，可以得出模型的殘差值基本呈正態(tài)分布。進一步驗證模型的構建是有效的。

2.共線性優(yōu)化

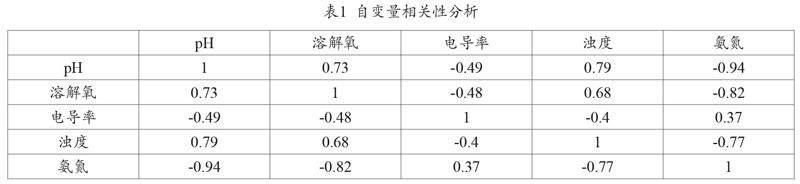
首先可以對指標開展相關性檢驗，相關性檢驗可以檢驗指標之間是否存在明顯的相關關系。根據(jù)相關性檢驗結果，相關性統(tǒng)計如表1。

所選指標中pH和濁度呈正相關，pH和氨氮呈正相關，溶解氧和氨氮呈負相關，濁度和氨氮呈負相關，因此所選指標存在共線性。且氨氮與其他3個指標存在明顯的相關性，考慮先將氨氮作為待剔除指標，需進一步借助VIF與容忍度驗證共線強度檢驗。根據(jù)R輸出的結果如表2，在考慮剔除指標時，由于pH和氨氮存在較大的共線性關系，這也與實際相符，氨氮與水形成弱堿，氨氮的濃度越高，水中的pH值越大，因此優(yōu)先考慮剔除其中一個指標，剔除指標方法結合顯著性、容忍度、VIF（方差膨脹因子）進行判斷。一般認為VIF大于10，容忍度小于0.1，說明自變量之間存在顯著的共線性，這里將VIF較大的氨氮進行剔除。

VIF越大，容忍度越小，共線性越嚴重。將指標氨氮剔除后，重新建立模型，再次對模型進行容忍度和VIF檢驗，輸出結果如表3，自變量容忍度均大于0.1，VIF小于10。新的模型R²變?yōu)?.9581，較之前無明顯變化。

3.逐步回歸驗證

本文采用赤池信息量準則（AIC）進行逐步回歸分析，得到最小AIC組合為：pH、溶解氧、濁度、電導率。最終表明無需再剔除指標，模型方程得到確認。

最終模型方程為：

y=1.576793-0.103860x₂+0.967248x₃-0.003806x₄+0.018848x₅

（二）擬合檢驗

通過對溶解氧的實測值與預測值的相對誤差進行比較，以及y和yi之間的相對誤差分析，根據(jù)圖2曲線圖可以看出，溶解氧實際值和預測值擬合度良好，擬合值和實測值呈顯著的正相關性，說明多元線性回歸模型具有較高的精準度，對歷史值的預測較好。

五、結果驗證

通過多元線性回歸模型對水站2022年8月—12月每日溶解氧數(shù)據(jù)進行預測，得到預測值與實測值的擬合結果如圖3所示，預測結果誤差核密度如圖4所示。

從相對誤差核密度圖可看出，多元線性回歸預測平均相對誤差近似為0.328%（接近于期望0），最大相對誤差為14.5%，75%誤差分位數(shù)為3.2%，90%分位數(shù)為5.4%，95%分位數(shù)為7.8%，即95%的情況下，誤差精度在8%以內(nèi)，說明多元線性回歸模型滿足水質(zhì)預測預報的精度要求，模型預測效果較好，為水質(zhì)預測預警提供了數(shù)據(jù)支撐。

六、結語

1.本研究利用水站歷史自動監(jiān)測數(shù)據(jù)，基于多元線性回歸分析法，建立多元線性回歸模型對溶解氧進行預測，結果表明，在此站點，多元線性回歸模型對預測溶解氧濃度具有較高的精確度。

2.利用本研究建立的模型對水站2022年8月—12月每日溶解氧數(shù)據(jù)進行預測，驗證數(shù)據(jù)顯示模型滿足水質(zhì)預測的精度要求，預測效果較好，為水質(zhì)預警預測提供了數(shù)據(jù)支撐。

3.該方法建模過程簡單，結果直觀，精確度高，大幅度減少了計算時間，可在其他斷面推廣和應用。

參考文獻

[1]王婷婷，李慧.水質(zhì)監(jiān)測實驗室的安全管理[J].資源與環(huán)境，2022，48（2）：190-192.

[2]張穎，高倩倩.基于灰色模型和模糊神經(jīng)網(wǎng)絡的綜合水質(zhì)預測模型研究[J].環(huán)境工程學報，2015，9（2）：537-545.

[3]石月.基于時間序列分析的松花江流域水質(zhì)預測[D].哈爾濱：哈爾濱師范大學，2015.

[4]國務院.國務院關于印發(fā)水污染防治行動計劃的通知[EB/OL].（2015-04-16）[2023-01-17] .http：//www.gov.cn/zhengce/content/2015-04/16/content_9613.htm.

[5]申杰，潘楊，黃勇.城市地表水環(huán)境評價方法綜述[J].環(huán)保科技，2011，17（4）：41-45.

作者單位：中國人民大學