內波與地形作用過程研究
王春凌 王寅

摘要:內波是分層水體中普遍存在的水動力現象,破碎產生的湍流是打破水體層化的重要機制之一。本文采用數值模擬技術模擬研究了內孤立波與典型大陸坡的相互作用過程。
關鍵詞:破碎;內孤立波;能量耗散;地形
基金項目:國家自然科學基金青年基金項目
項目編號:52009087、52109090
基金項目:浙江省自然科學基金公益項目
項目編號:LGF19E090005
基金項目:中國博士后科學基金面上項目
項目編號:2022M721426
一、研究背景
內波是密度層化水體中內界面波動現象,在遭遇地形或障礙物時,內波會發生不同程度的破碎,激發的紊流有助于局部水體混合,改善局部水質,無規律的水質點運動作用于結構,使結構體發生“渦振”,破壞結構穩定性。內波破碎和誘發機制復雜,Saffarinia和Kao等人用數值方法模擬了兩層流體中內孤立波在平坦地形上傳播和破碎,發現當波面指點流速超過內波相速度時,下層水體被卷躍至上層,內波發生破碎且此時波幅為上層水深的2.65倍,指出波的破碎是對流不穩定導致的。Vlasenko和Hutter對內孤立波與大陸架作用過程模擬發現,淺水效應使內波波面不斷陡峭直至翻轉、破碎,此時的破碎由對流不穩定引起,隨后Afansyev和Peltier、Legg和Adcroft、Klymak和Pinkel等也得到類似結論。Barad 和Fringer等人的研究則指出,剪切不穩定同樣可導致內波發生破碎,在內重力波和加速剪切流的傳播過程中,剪切不穩定的發生取決于剪切流的加速度,即當加速度較小時,內波會因為剪切不穩定發生破碎,且內波誘發紊流產生的水體混合效率與不穩定剪切相關。然而,自然條件下內波破碎通常是對流不穩定和剪切不穩定共同作用的結果,不穩定特征與波幅和傳播方向相關。劉國濤等人對內波在白噪聲干擾下引起的不穩定現象進行分析,結果顯示,靜力不穩定最先出現,持續時間較長,隨后剪切不穩定和對流不穩定相繼出現。
關于內波破碎判據,Helfrich將離岸最遠的初始湍流斑點出現位置定義為內波破碎位置,并得出當a/d≥0.4±0.1(a是斜坡起點處波幅,d是破碎位置的下層水深)時,內波發生破碎。Vlasenko和Hutter認為:當無量綱振幅a*=am /(Hb-Hm)滿足a*=0.8/γ+0.4時,如果Hs<Hb,內波的背風面在斜坡上破碎,反之會以頻散尾波的形式繼續傳播。Fringer和Street認為內波破碎發生的不穩定主要與界面厚度相關,并給出kδ<0.56時(k為水平波數,δ為界面厚度),內波波峰和波谷出現Kelvin-Helmholtz(K-H)不穩定;當0.56≤kδ<2.33時,初始不穩定為剪切不穩定;當kδ≥2.33時,由于界面厚度較大無法形成K-H不穩定,為對流不穩定。Troy的研究結論認為當0<kδ<0.66時,擾動長度僅隨界面厚度變化,具有最大增長率的擾動得以充分發展,形成K-H滾動,內波破碎主要是剪切不穩定引起;當0.66≤kδ<0.3時,擾動增長率減小,剪切不穩定不能充分發展;當kδ≥1.3時,剪切不穩定不可能發生,內波不發生破碎。
Barad和Fringer分別給出不穩定性的判據條件:Richardson數Ri小于0.1;σT>5, T是Ri數<0.25的時間長度,σ是擾動在此時間內的平均增長率;Lw/L>0.86, Lw是Ri<1/4區域的長度的一半,L是內波的半寬度。近年來,有研究者提出內波破碎與地形坡度和內波坡度的比值相關,比值越小,破碎摻混越劇烈。相對于斜坡,孤島地形導致的內波破碎通常用阻塞系數ζ(ζ=(a+H1)/(H1+H2+hs),a是波幅,H1、H2分別為上下層水深,Hs是障礙物高度描述將內波與障礙物作用程度分為弱作用(ζ<0.55),適度作用(0.55<ζ<0.7)和內波破碎(ζ>0.7),各研究者根據阻塞系數的取法不一致,結論有所不同。對于三層分層流體中的第二模態內波,當阻塞系數0.2<B<2(B=am/?h, am為波幅,?h為內界面到地形頂面的高度)時,內波將完全破碎分解。
針對內波能量計算,多數研究者的論文中采用下式估算內波勢能:
; (1)
此法簡單易行,只需勾勒出波面形態即可進行估算,多用于物理水槽試驗中。然而,在內波破碎劇烈情況下,用此方法進行勢能估算誤差較大,一方面,混合區界面無法準確捕捉;另一方面,作用過程形成的小尺度和微尺度內波難以被精確刻畫。
綜上所述,內波破碎仍有兩個問題有待進一步探討:內波破碎過程特征尚未確定;傳統內波勢能計算公式存在一定局限,真實能量的損耗、轉化需進一步分析。
本文通過數值模擬方法,系統研究典型地形與內波作用過程,分析水體剪切不穩定和對流不穩定發生機制,確定內波與大陸架地形破碎的基本特征。同時,為探求更為精確的內波能量損失值,對用式(1)的估算值進行分析和修正,為理論模型用于實際工程提供可靠的參考及修正依據。
二、數學模型
(一)控制方程
基于連續介質假設,描述不可壓縮粘性流體的連續方程和動量方程為:
; (2)
;? (3)
式中,ui 和xi分別是i方向的速度和坐標;ρ是壓強;是流體密度,本研究中清水密度取值1000kg/m3,鹽水密度取值為1030kg/m3;t是時間;μ是流體動力黏度;gi是i方向加速度,豎直方向取值為-9.8m/s2,其他方向取值為0;si是動量源項。
通常將內波概化為兩層分層流體的多相流問題,數值計算中通過求解體積分數對當地物理量進行更新:
且? ?; (4)
式中,λ為更新的物性值,例如密度,Φm和λm分別為第m相的體積分數和相屬性值。對于不可壓縮兩相流,只需計算某一相體積分數,余下即為另外一相。
本文采用大渦模型求解控制方程,濾波后的控制方程和體積分數輸運方程為:
(5)
τij為亞格子應力項,是可解尺度運動與亞格子尺度運動之間的動量輸運,需進行模化處理,采用擬序渦結構模型封閉方程。
(二)求解方法和邊界條件
采用結構化網格對計算區域進行離散,通過分步法(Fractional Method)分別求解對流項、擴散項和壓力項,方程如下:
; (6)
; (7)
; (8)
式中,“*”和“**”分別代表對流步和擴散步求解的中間物理量,“n”代表當前時刻,“n+1”代表新時刻。在得到流場后,求解體積分數(Volume Of Fraction,簡稱“VOF”)輸運方程:
; (9)
同時,由式(3)更新本地密度。
邊界是否設置合理直接關系計算收斂和數值準確性。本文中水槽自由液面采用垂向速度為零,其他方向速度梯度為零;底部采用固體壁面邊界;入流邊界采用滑移邊界;出流采用Sommerfeld邊界,避免入射波反射。
應用兩層流體內波關系式:(h1+a) U1 = (h2-a) U2 = c0η, 得到上下層水體的理論流速值。其中,η為波面高; h1和h2分別為上下層水深;U1和U2分別為上下層理論平均流速。基于波面函數和流速理論解,采用邊界造波方法進行數值造波,與傳統方法相比,該方法保證了完整的波形,便于波能計算。
三、模型實驗及結果
(一)模擬試驗
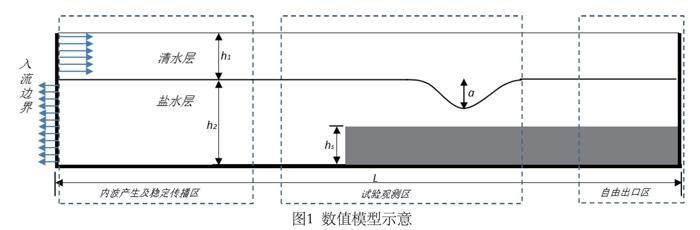
試驗在一數值水槽中進行,水槽長10m、寬0.5m、高0.4m,圖1為數值水槽示意圖。在入流邊界定義流速進行造波,速度如何取值見上文。hs為大陸架高度,h1和h2分別為清水層和鹽水層厚度,清水密度為1000kg/m3,鹽水密度為1030kg/m3,水槽右側為自由開邊界,防止反射波影響試驗觀測區。
(二)模擬結果
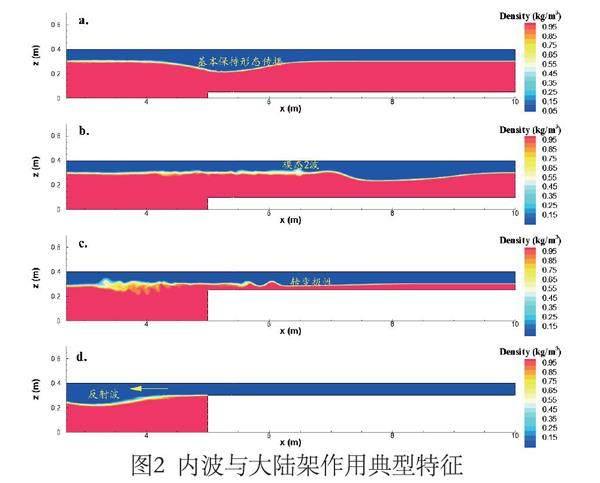
模擬實驗揭示了下凹型內孤立波與大陸架地形相互作用過程,該過程可分為三種情況:當地形高度與內分界面距離較大時,內孤立波不受影響繼續保持原有波形前行(圖2a)。隨著地形高度增加,在內孤立波接近地形過程中,由于局部水流增大波面發生不同程度的扭曲變形甚至破碎產生紊流。因此,內孤立波也被稱為水體的天然攪拌器。局部的混合不僅利于上下層水體打破分層將富含氧的水體輸送到底層,其形成的第二模態內波(圖2b)還可實現界面處的物質遠距離輸運。除此之外,模擬研究發現與地形作用過程中存在內孤立波轉變極性的情況(圖2c),這主要取決于地形上方的上下層水深比。根據KdV理論,h1/h2的值偏離1,其非線性越明顯,表現在波形上是波幅越大;反之,表現為彌散作用占主導,即波形越變得扁平。
當地形高度等于或高于分層界面時,內孤立波幾乎完全反射(圖2d),但反射系數與大陸架坡度有一定相關性,這一點在Chen等人(2007)的研究中已得到證實。圖3中為直角大陸架和非直角大陸架上內孤立波誘發的流場,圖中內孤立波向右傳播,引起的下層水體流向與波的傳播方向相反,很明顯在直角大陸架的迎波面有逆時針的漩渦形成,原因是直角處的水體受剪切;當坡面較緩更貼合水流特性,坡底水體受剪切不易形成漩渦。漩渦的存在大大增加了對底部的剪切,造成地形不同程度的侵蝕,消耗的能量也相對較多。圖4為直角大陸架和非直角大陸架對內波能量消耗的對比圖,從圖中可以看出,直角大陸架消耗的內波能量高于帶坡度大陸架地形約1.5%,整體能量損失隨地形高度先增后減且符合線性規律,峰值位置出現在km≈0.3處,大小約為初始能量的20%~25%。
四、結語
本文采用數值試驗的方法對內波與典型大陸架地形的相互作用過程進行了模擬,通過分析流場和能量計算得到如下結論:
內波與大陸架作用的演變過程與地形高度相關,當地形高度小于下層水深1/6時,內波幾乎不受地形影響保持原有形態前行;當高度超過此數值,內波的演變還與地形上的上下層水深比相關,根據該比值偏離1的程度發生裂變和轉變極性。同時,伴隨內波第二模態出現,地形上方水深比大于1時,第二模態波跟隨反射波;反之,模態二波跟隨透射波。
與地形作用過程損失的能量與地形高度相關,隨地形高度的增加出現先增后減的趨勢,且在無量綱參數km=0.3時,耗散能量達到峰值,約占初始能量的20%~25%。
與非直角大陸架相比,直角大陸架消耗的能量偏多,主要原因是與地形作用過程中在坡腳產生旋渦結構,該結構加大了水體剪切,從而加速能量損耗。
參考文獻:
[1]Aghsaee,P.and L.Boegman.Experimental Investigation of Sediment Resuspension Beneath Internal Solitary Waves of Depression.Journal of Geophysical Research:Oceans,2015,
120(05): 3301-3314.
[2]Zhu,H.,L.Wang,and H.Tang. Large-eddy Simulation of the Generation and Propagation of Internal Solitary Waves.Science China Physics,Mechanics & Astronomy,2014,57(06):1128-1136.
[3]Saffarinia,K.and T.W.Kao,A Numerical Study of the Breaking of an Internal Soliton and Its Interaction with a Slope.Dynamics of Atmospheres and Oceans,1996,
23:379-391.
[4]Vlasenko,V.and K.Hutter.Numerical Experiments on the Breaking of Solitary Internal Waves. Journal of Physical Oceanography,2002,32:1779-1793.
[5]Vlasenko,V.I.and K.Hutter.Generation of Second Mode Solitary Waves by the Interaction of a First Mode Soliton with a Sill.Nonlinear Processes in Geophysi-cs,2001,08(4/5):223-239.
[6]Barad,M.F.and O.B.Fringer.Simulations of Shear Instabilities in Interfacial Gravity Waves. Journal of Fluid Mechanics,2010.644:61-95.
[7]劉國濤,尚曉東.海洋內波能量耗散的數值研究[J].海洋石油,2019,39(01):82-87.
[8]Helfrich,K.R.Internal Solitary Wave Breaking and Run-up on a Uniform Slope. Journal of Fluid Mechanics,1992,243:133-154.
[9]Arthur,R.S.and O.B.Fringer.The Dynamics of Breaking Internal Solitary Waves on Slopes. Journal of Fluid Mechanics,2014,761:360-398.
[10]Maderich,V,et al.Numerical Simulations of the Nonhydrostatic Transformation of Basin-Scale Internal Gravity Waves and Wave-Enhanced Meromixis in Lakes, in Nonlinear Internal Waves in Lakes,2012:193-276.
[11]Talipova,T,et al.Internal Solitary Wave Transformation Over a Bottom Step: Loss of Energy. Physics of Fluids,2013,25(03):032110.
[12]Liu,A.K,et al.Generation and Evolution of Mode-two Internal Waves in the South China Sea.Continental Shelf Research,2013(59):18-27.
[13]Chen,C.Y.Amplitude Decay and Energy Dissipation Due to the Interaction of Internal Solitary Waves with a Triangular Obstacle in a Two-layer Fluid System:the Blockage Parameter.Journal of Marine Science and Technology,2009,14(04):499-512.
[14]Wang,C.,etal.Numerical Modeling of Energy Dissipation of Internal Solitary Waves Encountering Step Topography.Ocean Engineering,2022,259:111853.
[15]Wang,C.L.,L.L.Wang,andH.W.Tang,Depression Internal Solitary Wave Interaction with Submerged Obstacle.Journal of Environmental Biology,2016,37(05):1217-1223.
[16]Chen,Y.C.,et al.Wave Propagation at the Interface of a Two-layer Fluid System in the Laboratary.Journal of Marine Science and Technology,2007,15(01):8-16.
作者簡介:王春凌(1985),男,安徽省安慶市人,中級講師,博士學歷,主要研究方向為水力學。

