車內發動機噪聲主動降噪辨識方法及DSP實現

張程鵬，張士強，李 浩，王 石，李 允，曹蘊濤

（中國第一汽車集團有限公司，吉林 長春 130011）

1 研究現狀

汽車主動降噪技術（Active Noise Control,ANC）在近兩年的國內汽車市場發展迅速，截至2022 年1 月，國內汽車市場有25 個品牌共63 款車型具備主動降噪功能，如合資品牌的凱迪拉克、林肯、本田、別克等，國產品牌的紅旗、長城、吉利、大通等。合資品牌的產品主要由BOSE、哈曼、Silentium、松下等供應商提供，國內相關企業也逐步在國產車型上進行量產。

以乘用車四缸發動機為例，發動機噪聲的能量集中在二、四、六階，屬于低頻噪聲，傳統被動降噪方法對低頻噪聲的隔吸聲并不理想。由于低頻噪聲波長較長，相位變化慢，根據聲波干涉原理，主動降噪技術對低頻噪聲的抵消有明顯優勢。

1.1 國外研究進展

2017 年，HASEGAWA 等人提出虛擬麥克風技術用于修正人耳不在最佳降噪位置的問題，但增加的傳遞函數會占用更多的計算資源[1]。2018年，CHENG 等改進了窄帶噪聲的次級傳遞函數的辨識方法，采用一系列自適應濾波器，針對不同頻帶的次級傳遞函數特征完成建模，降低誤差并提高了收斂速度[2]。

1.2 國內研究進展

2017 年，MA 等人在利用附加隨機噪聲法進行次級路徑建模，采用無限脈沖響應（Infinite Impulse Response, IIR）濾波器減小了寬頻隨機噪聲對殘余噪聲功率的影響，從而提高了系統收斂速度和建模精度[3]。2018 年，ZHAO 等人提出一種將次級路徑離線識別和在線識別相結合的新型方法，可以使有源噪聲控制系統達到更快更穩定的效果[4]。2019 年陳祥君在陷波最小均方算法（Least Mean Square, LMS）的基礎上提出陷波延時LMS 算法，從而將參考信號的延時操作取代傳統陷波LMS 算法中次級路徑傳遞函數與參考信號的卷積操作，大幅降低算法的計算量[5]。2020 年肖夢迪提出一種基于能量比調控的次級通道在線建模有源噪聲控制算法，能獲得較快的建模收斂速度[6]。2021 年來昊采用誤差濾波LMS 算法進行控制，噪聲煩惱度明顯降低[7]。WANG 等人對于窄帶有源噪聲控制系統提出了一種新的頻率估計方法，該方法不需要原始信號的先驗信息，并且大大改善了收斂特性[8]。馮智睿基于虛擬誤差傳感的方法，擴大了主動降噪的有效降噪范圍[9]。2022年吳禮福采用一種自校正自適應算法，通過串聯多個低階濾波器以簡化濾波器階數選擇并降低計算復雜度，同時獲得與濾波x 最小均方算法（Filtered-x Least Mean Square, FxLMS）相當的降噪性能[10]。

2 FxLMS 算法原理

2.1 LMS 算法理論

LMS 是以誤差信號的均方根最小為目標進行計算，采用有限脈沖響應（Finite Impulse Response,FIR）濾波器，其輸出只和當前時刻的輸入以及之前若干時刻的輸入有關。

n時刻輸入X(n)為

n時刻濾波器權系數W(n)為

n時刻濾波器輸出y(n)為

LMS 算法基本思路為控制權系數W(n)沿著梯度方向搜索實現均方誤差ε最小，下面簡述公式推導過程。

期望信號d(n)與輸出信號y(n)相減：

均方誤差ε為

權系數更新為

2.2 自適應陷波法原理

目前車內發動機主動降噪的原理主要采用基于FxLMS 的自適應陷波濾波算法，自適應陷波算法是人為構造正弦頻率信號作為參考信號，通過LMS 算法實現對某一目標頻率噪聲的抵消，自適應陷波濾波算法框圖如圖1 所示，其中x(n)為噪聲源，d(n)為誤差麥克風噪聲處原始噪聲，X0(n)為正弦參考信號，w0(n)和w1(n)為權系數，y(n)為次級聲波，e(n)為誤差信號，S(z)為次級傳遞函數，S0(z)為次級傳遞函數估計。由于自適應陷波算法結構簡單、計算量較小，并受限于汽車成本，因此，工程應用廣泛采用自適應陷波算法。

圖1 自適應陷波法原理圖

3 仿真模型

本文采用 Simulink 建立了自適應陷波模型，采集實車的加速噪聲及轉速數據，對轉速進行平滑處理，比較降噪前后的仿真結果，對該算法進行了驗證，結果符合預期。

在Simulink 仿真環境中建立的主動降噪仿真模型如圖2 所示。仿真模型采用車內原始加速噪聲數據及發動機轉速數據，根據轉速構建正弦參考信號。為滿足LMS 算法的收斂的要求，其中可調節的參數包括迭代步長、泄露因子、信號幅值等，運行模型能夠驗證陷波算法的有效性。但需要注意的是，純數值仿真無法模擬真實次級路徑與次級路徑估計的差異。

圖2 自適應陷波仿真模型

某四缸機車型加速工況駕駛員左耳噪聲仿真效果對比如圖3 所示，仿真結果驗證了仿真模型和算法的有效性。圖3 上半部分為原始噪聲，圖3下半部分為仿真降噪后的效果，可以看出發動機二階噪聲明顯降低，驗證效果符合預期。

圖3 仿真降噪前后對比圖

4 掃頻辨識方法

次級路徑的辨識過程有離線和在線兩種方法，其中離線建模是在系統未工作時，對次級路徑的傳遞函數用FIR 濾波器進行估計，對于車內主動降噪系統的次級路徑建模，當硬件系統的位置和參數確定后，次級路徑特性保持不變，因此，車內主動降噪研究普遍采用離線建模的方式估計次級路徑。

次級路徑的辨識是數字信號從發出到再次采集的過程，主要體現了信號的延時和相位變化，包含了硬件電路、揚聲器、空氣、麥克風的完整的信號傳輸路徑。實現過程如圖4 所示。

圖4 離線辨識次級路徑過程示意圖

目前公開的研究成果對次級路徑建模采用白噪聲信號進行辨識過程的計算，本文采用一種掃頻方法進行次級路徑離線建模工作，通過合成降噪頻率區間的正弦波進行掃頻辨識，估計出次級路徑的時延系數的擬合曲線，在進行控制程序濾波時調用。該方法的優點在于采用連續變化的頻率進行建模，頻率范圍和運行時間可根據研究或工程需要靈活調整。

掃頻信號的計算推導如下：

頻率函數為

式中，f0為初始頻率；k為增長系數。

式中，f1為終止頻率。

則計算相位函數需要對f(t)積分，得

所以正弦掃頻的函數為

采用上述推導的掃頻公式結合揚聲器的頻響特征，研究過程設定掃頻范圍為50～300 Hz，時間為10 s。在車內環境下進行次級路徑的辨識結果如圖5 所示。

圖5 次級路徑辨識結果

5 DSP 控制器與實車匹配

DSP 芯片是一種特別適合于進行實時數字信號處理運算的微處理器，具有獨立的硬件乘法器，乘法指令可在單周期內完成，使卷積、數字濾波、相關運算、矩陣運算等算法中的大量乘法運算速度加快。

本文使用的硬件控制器的DSP 芯片型號為ADI 21489，使用C 語言對控制器進行固件開發及主動降噪算法移植。控制器具備麥克風信號讀取、控制器局域網（Controller Area Network, CAN）信號讀取，數據處理及驅動揚聲器發聲等功能，可以滿足研究工作的需求，進行主動降噪效果驗證。本節內容對DSP 控制器與實車的匹配工作進行介紹，包括硬件接口匹配、發動機轉速信號接口匹配、發動機轉速與控制器程序匹配。

5.1 硬件接口匹配

本研究采用原車線束進行音響系統與控制器的匹配，通過以下過程完成控制器與原車揚聲器的匹配工作。實物效果如圖6 所示。

圖6 控制器接口及匹配

參照原車功放的針腳接口定義確認原車線束端的電源、揚聲器線束位置；根據控制器端的接口定義，確認控制器端的電源、揚聲器、CAN、麥克風的針腳，通過接插頭線束引出；通過線端的接插件，將原車線束定義與控制器端的線束定義對應連接。

5.2 發動機轉速與控制器程序匹配

根據自適應陷波算法的原理，需要轉速信號生成主階次頻率的參考信號。從車載診斷系統接口（On Board Diagnostics, OBD）引出CAN_H、CAN_L 針腳；使用CAN 分析儀連接并確認讀出正確的發動機轉速信號；引出信號接入控制器；修改微控制單元（Micro Controller Unit, MCU）部分程序代碼，根據原車OBD 文件修改發動機轉速信號對應的地址、掩碼、高低位、精度和偏置量。將修改好的程序刷入控制器的MCU 中，通過控制器的上位機可以顯示出當前發動機的轉速數值，即完成了發動轉速與控制器的程序匹配。

主動降噪程序具備了在實車環境下進行閉環驗證的硬件條件。控制程序能夠在DSP 上運行，以發動機轉速為前饋信號、麥克風誤差信號作為反饋信號，進行主動降噪功能驗證。

6 實車布置與測試結果

6.1 車內主動降噪的硬件布置方案

降噪麥克風布置在副駕駛頭枕位置，控制器布置在后備箱內，驅動右前車門低音揚聲器發聲，降噪麥克風布置在副駕駛頭枕處。測試使用的標準傳聲器布置在與降噪麥克風相同的位置，如圖7所示，其余測試設備及測試人員均在后排。

圖7 誤差麥克風與標準傳聲器布置圖

6.2 試驗結果

在轉轂試驗室進行主動降噪功能測試，用掃頻方法得到次級路徑的系數（圖5），將系數導入降噪控制程序中進行主動降噪性能測試。測試工況選擇擋位鎖定在二擋，緩加速20 s，發動機轉速從1 000 r/min 上升至4 000 r/min。通過標準傳聲器采集噪聲數據并分析發現，300 Hz 以內的發動機二、四、六階降噪效果明顯，30～300 Hz 的Overall（OA）值最大降低4 dB。試驗結果如圖8所示，其中虛線為原始噪聲，實線為開啟主動降噪的效果。

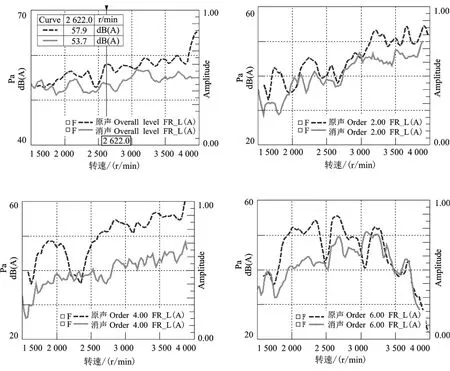
圖8 主動降噪開關前后對比圖

6.3 結果分析

測試結果證明主動降噪效果明顯，證明掃頻辨識方法行之有效。根據主動降噪算法的原理，對于較突出的頻率噪聲有明顯降噪效果，并且主觀感受明顯；反之若發動機階次噪聲控制的很好，階次噪聲較小，則主動降噪的降噪幅度較小，主觀感受相對微弱。本試驗樣車的發動機階次噪聲較為突出，測試結果表明主動降噪技術是一種有效的發動機噪聲解決方案。

7 結束語

本文首先介紹了主動降噪的國內外研究進展以及部分原理，其次通過仿真模型驗證了算法的可行性，最后從工程角度介紹了主動降噪系統從線束連接、控制器通訊、硬件布置、DSP 代碼控制實現過程。本文提出了一種采用掃頻辨識的方法進行發動機主動降噪的次級路徑研究，采用50～300 Hz 區間的掃頻信號完成辨識，并使用DSP 控制器在車內驗證了主動降噪的效果。測試結果表明50～300 Hz 的發動機二、四、六階降噪效果明顯，聲壓級 OA 值最大降低4 dB。試驗結果驗證了掃頻方法用于次級路徑建模是可行的，可根據需要靈活調整，是一種切實可行的方法。