前有“蘊蓄” 后有“突破”
——單元整體視角下《平行與垂直》教學與思考

文|徐曉良 黃陳辰

一、剖析：直面現狀，尋圖形教學的癥結點

在日常教學中，雖然學生掌握了相關的概念，但是并不能應用概念來識別圖形，對圖形本質特征以及圖形之間的區別與聯系的理解還不到位。以2019年嘉興市五年級上冊期末檢測卷中的一道題為例：下圖中兩個正方形的邊長分別是5 厘米和4 厘米，圖中的四邊形ABCD 是（ ）形。全市學生的正確率僅為38.9%。

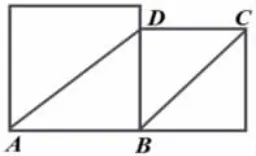
進一步對城區學校五年級某班進行第二次測試，改編問題為填空加論述：有一大一小兩個正方形，圖中的四邊形ABCD 是（ ）形，你的判斷依據是什么？學生填空的正確率為36.6%。進一步訪談發現學生錯誤的原因是：第一感覺看著不像梯形，63.4%的學生覺得看著是平行四邊形。

可見，學生在系統學習了單元內容后仍依賴于“直觀感知”區分圖形，沒有從概念本質出發。而在日常學習中，標準圖形刺激遠大于變式圖形刺激，學生憑表象感知來識別圖形，在變式圖形的計數與判斷上容易導致錯誤的發生。

二、調查：學情分析，探知識生長的初始點

基于生活經驗，學生對生活中的平行與垂直現象有一定的感知。為深入了解學生關于兩條直線的位置關系以及本單元最難掌握的梯形的已有認識，隨機抽取了本校40 名學生進行了前測（如表1）。

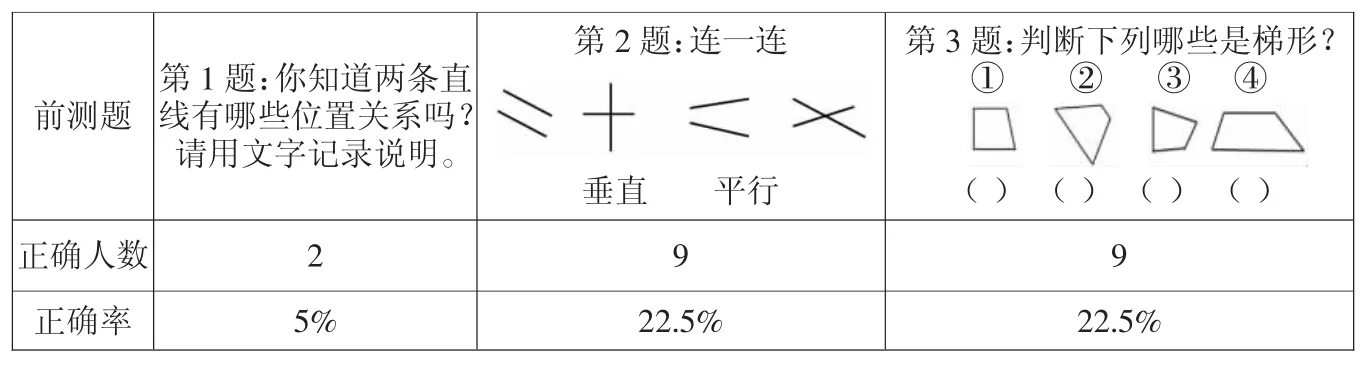
表1 《平行與垂直》教學前測

根據前測結果，結合對學生的訪談可知，對于第1 題，僅有兩名學生正確作答；對于第2 題，學生對平行有直觀感知，但對何為“垂直”基本沒有概念；對于第3題，大多數學生對非標準式的，或者旋轉后位置發生改變的梯形判斷有難度，學生基本是憑直覺大致看一眼判斷，誤認為①②④不是梯形。

可見，學生對于有一定生活經驗的“平行”能正確識別，而對于抽象性較強的“垂直”，以及與生活經驗匹配度不高的特殊四邊形，會因為思維固化，或者缺乏同化經驗而不能靈活遷移。因此在建構概念時要根據學生的認知能力和思維水平從低起點出發。

三、解讀：前延后伸，定單元學習的核心點

作為從一維的線向二維的面過渡的兩個重要概念，“平行與垂直”以線段、射線、直線和角的學習為認知基礎，也是后續平行四邊形、梯形、三角形的概念及面積計算，長方體、正方體知識學習的重要根基。《義務教育數學課程標準（2022年版）》對此要求能辨認同一平面內兩條直線是否平行或垂直。對比人教版、蘇教版、浙教版、北師大版教材（如表2），可以發現各版本教學中都以問題為先導，引領學生開展探索交流。雖然各版本呈現方式有所不同，對兩個核心概念的認識順序各異，但都重視學習素材的直觀呈現，借助動態演示或具體操作，幫助學生內化概念本質。

表2 各版本《平行與垂直》教學內容對比

聚焦本單元重點內容平行四邊形和梯形，作為二維圖形的再認識內容，要求進一步從圖形的要素、名稱及關系來描述其特征，既是從邊和角的要素進行圖形認知，也是從高和底的角度對“面”感知。如何引導學生對平行四邊形和梯形形成結構化的認識，并能運用猜想驗證、類比遷移、特征分類等加深對圖形本質特征和圖形之間關系的深度理解，實現從直觀感受圖形特征到探索圖形本質屬性的成長與跨越，是我們本單元教學中的核心點和思考點。

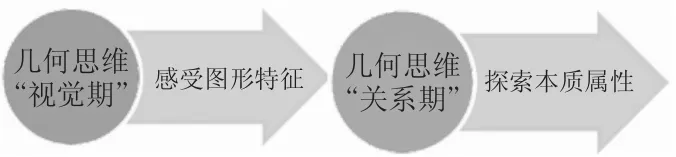
四、統整：蘊蓄突破，架“表象———本質”的著力點

基于以上分析與思考，嘗試將“認識平行和垂直”和“認識梯形”進行重組，將本單元最難認識的梯形在“平行和垂直”的教學中進行滲透，將四邊形教學貫穿單元教學的始終。第一課時從探究圖形出發，到特殊圖形中尋找平行、相交、垂直不同的位置關系，再回到對圖形的再認識，通過系列化的學習任務，引導學生認識圖形與要素、圖形與概念之間的關系，明確數學知識之間的聯結方式，促進學科關鍵能力的提升。

（一）圖形解構，直觀化中理解概念

從直角梯形引入，依托直觀化的素材，通過“梯形解構——共性尋找——趣味命名——深入辨析”四個環節，凸顯核心概念。在這一環節中學生在理解平行和垂直概念的同時，對梯形的特征有了第一次初步的感知。從梯形分解引入，為后面進一步“還原”梯形研究其本質特征做鋪墊。

首先，將梯形進行解構，分解出兩組對邊、四組鄰邊。將每一組鄰邊所在的直線向兩端無限延長，引導學生先想象延長后形成的圖形，再PPT 演示驗證直線延長過程，以此提升學生的空間想象能力。

結合延長后所形成的圖形，引導學生從四組相交的情況中找共同點，根據學生多樣化的回答，如從“角”（有的圖形形成了兩個銳角和兩個鈍角，有的圖形形成了四個直角；這些圖形的對角都相等），從這些圖形都有一個交叉點（即兩條直線的交點）等多角度的思考中培養學生的發散思維。

以“趣味命名”方式凸顯核心概念。先讓學生童趣化“命名”，然后揭示數學家的定義，形成“相交、交點、垂直”等概念，進一步獲得鄰邊所在的直線都相交的結論。特別地，對于“垂直”這個新名詞，抓住“兩條直線相交成直角”的本質特征，經歷垂直的驗證過程，積累活動經驗。

借鑒學習鄰邊的經驗，適時拋出問題“對邊中是否也有這樣的相交現象”，借助《學習單》探究對邊所在直線的兩種不同情況，經歷自主思考、作品交流、深入辨析的過程，通過延長的方法得到左、右對邊所在的直線都相交的結論，完善學生對相交的認知。針對上、下底所在直線的這一組對邊，讓學生解釋一定不相交的理由，發現“永不相交———平行”的現象，也讓學生對平行線間的距離處處相等有一定的感知。

（二）聯結重組，結構化中突出本質

在學生知曉了平行和垂直的概念之后，讓學生在生活中尋找舉例，引導學生用數學的眼光觀察世界。對于“互相平行、互相垂直、垂足”等概念的學習，讓學生以自學釋疑的方式，在自學課本內容圈一圈、畫一畫的基礎上，說一說學到了什么，再聚焦核心問題解析重點，突破難點，讓新知的習得順理成章。

練習的設計從線到面，層層遞進。練習一是對平行與垂直的鞏固，涵蓋了延長后是否屬于平行或垂直的情況，也涉及兩條曲線的情況。針對學生易錯的④號圖形，讓學生展開辨析，抓住垂直本質特征進行判斷。

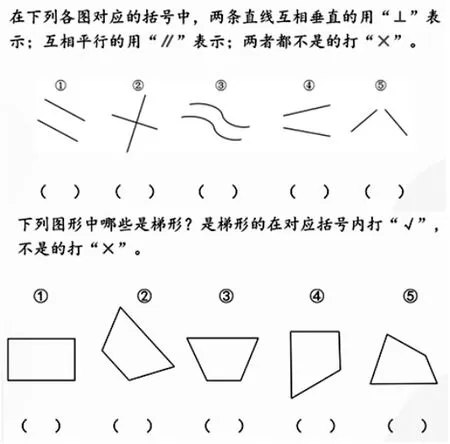
練習二是對梯形特征的梳理，尤其是非標準式的梯形和旋轉后位置發生改變的梯形的抽象，突出梯形“只有一組對邊平行的四邊形”這一本質屬性。學生認識了梯形的各種表現形式，留在腦中的梯形表象將更加鮮明，對梯形特征的理解也更加深刻。

練習的設計不僅指向學生深度理解平行和垂直的概念，還進一步運用概念抽象感悟梯形本質特征。這樣的結構打破了原來先認識平行和垂直，再研究平行四邊形和梯形的教學方式。在研究圖形時，發現一組對邊平行，一組不平行的四邊形是梯形，將表象感知與本質特征結合起來，使學生對圖形的識別不僅僅依賴于表象，更能從圖形本質特征進行理性判斷，實現從圖形本質意義上對梯形特征的第二次認識。

（三）多維建構，模塊化中貫通關聯

延伸第一課時重組教學路徑，從單元視角出發，站在結構化整合視角，關注知識間的關聯度，以板塊化的形式進行重組，形成更具有結構化、模塊化的“邊”“角”“高”“解決問題”“圖形變換”五大系列，讓知識的發生發展更貼近學情，有助于核心知識點的提煉與研究，促進學生思維的發展。（如表3）

表3 《平行四邊形和梯形》單元整合

其中，第二課時以“角”為切入點，猜想并驗證平行四邊形與梯形的特征，對梯形進行分類，完善對四邊形的認知。第三課時以“高”為主線，基于畫垂線與在平行四邊形和梯形中畫高在本質上的共通性，從畫垂線出發，將垂線段放置于圖形中，溝通高的定義，讓學生的學習融會貫通。第四課時從解決問題的角度出發，基于對畫垂線的掌握，用畫垂線的方式建構畫長方形的過程，將垂線段的性質應用于解決生活中的實際問題。第五課時以趣味化的內容，在圖形變換中尋找平行四邊形與梯形間的聯系與區別，在變換中體會四邊形容易變形的特征，讓學生的學習更具體驗感與挑戰性。

在后續深入學習平行四邊形后，再結合學生的生活實際，借助圖形轉換，類比分析，進一步認識梯形的特征并實現對它們的分類，通過研究圖形之間的聯系與區別，關注圖形與圖形之間的內在邏輯關系，多維度構建對梯形的全方位認識，完成對梯形特征的真正理解與應用，在三次認知中實現學生幾何思維能力的真正提升。