從“問題”到“結論” 從“一”到“一切”
廖晨輝
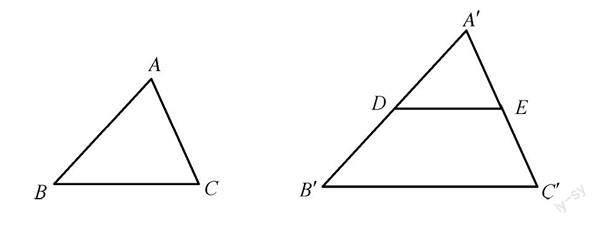
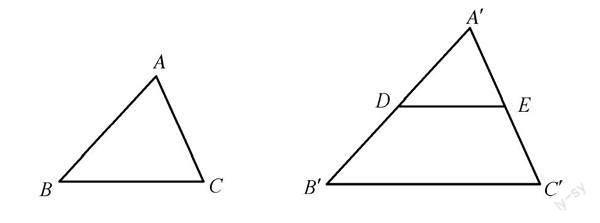

摘 要:抓住問題去探究結論,問題和結論往往存在著千絲萬縷的聯系,運用類比思想建構數學情境,從一道題到一類題再到問題和結論之間的轉化,優化數學課堂,整合提升.
關鍵詞:問題;結論;三角形相似;全等
《義務教育數學課程標準(2022年版)》中對于學生的應用意識和創新意識提出了更高的要求,不僅是跨學段的核心素養,也是跨學科的行為表現.在數學當中,題目千萬道,而唯有掌握其中的算理和邏輯推理,才是解決問題的正確途徑.從全等到相似的判定,既是順利過渡,其中又有著千絲萬縷的聯系,本文主要從相似的幾種判定方法談談從全等到相似的變換.
1 內容及學情分析
全等三角形是蘇科版八年級上冊第一章的內容,學生掌握了ASA、AAS、SAS、SSS、HL等數學證明方法,全等從三個角相等,三條邊相等到證明時只需要三個條件即可證明.相似三角形的探索是九年級下學期才開始的,學生的思維較八年級已經有了較大的發展,思考能力和邏輯推理較八年級有了更大的提升.如何從全等到相似?這些方法能不能無縫對接到相似?針對這些問題,以大單元的形式,筆者嘗試引導學生從全等出發,幫助學生打開探索相似三角形的大門.
2 教學過程
2.1 類比提出問題
前面我們學習了平行線分線段成比例,知道了相似與全等是一般與特殊的關系.那同學們看看全等的判定方法能用到相似上么?
教學說明:由平行得相似,通過在A′B′上截取A′D=AB,過D作DE∥B′C′得到△A′DE∽△A′B′C′,再利用ASA證明△ABC≌△A′DE,順利地從全等過渡到了相似.此刻引導學生了解到全等是相似的一種特殊情況,就是相似比等于1的那種,所以就可以把ASA、AAS里那個S去掉,從而得到只要有兩個角對應相等的兩個三角形是相似三角形,滲透了從特殊到一般的數學思想,在這個過程中讓學生充分探索全等和相似的聯系,并且發現相似的問題歸根到底還是得轉化為全等來解決.全等就是學生手中的那個“一”,是可以用來解決一切問題的那個工具.
2.2 合作探究問題
問題1:類比上述方法,全等中的SAS在相似的探索中如何表述?
問題2:你能用所學知識證明上述結論么?
教學說明:類比上述方法,在A′B′上截取A′D=AB,過D作DE∥B′C′得到△A′DE∽△A′B′C′,A′D∶A′B′=A′E∶A′C′,題目條件中AB∶A′B′=AC∶A′C′,因為A′D=AB,所以AC=A′E,再利用SAS證明△ABC≌△A′DE,再次驗證了全等在相似中的延續,學生的學習經驗得到了升華,進而為后續的推理做好鋪墊.
問題3:類比上述方法,全等中的SSS在相似的探索中如何表述?
問題4:你能用所學知識證明上述結論么?
教學說明:到了這兩個問題時,大部分學生已經可以自己推導證明了,運用類比的方法,在A′B′上截取A′D=AB,過D作DE∥B′C′得到△A′DE∽△A′B′C′,A′D∶A′B′=A′E∶A′C′=DE∶B′C′,又因為AB∶A′B′=AC∶A′C′=BC∶B′C′,所以AB=A′D,AC=A′E,BC=B′C′,從而利用SSS證明△ABC≌△A′DE,進而得到了兩個三角形相似.
3 教學反思
教師在教學時常常關注學生這道題懂了沒有,會不會做,但往往忽視了學生的思維和他的靈感.對于數學中的問題,往往存在著千絲萬縷的聯系,教學時課堂中的靈光一現或是學生腦中閃過的一絲困惑往往會被忽視.教材中的情境引入是教學必不可少的環節,在平時的課堂教學中教師要善于抓住學生的思維進行適時適當的探究,幫助學生建立模型,運用一類方法解決一切問題,這樣對于學生的數學學習是非常有幫助的.從問題到結論,不斷思考,層層遞進,觸類旁通,將知識內化,切實提高學生的思維和解題能力.
參考文獻:
[1] 李建華,胡軍.基于高階思維培養的中考數學專題復習課架構——以“相似三角形”專題復習課為例[J].數學通報,2022,61(6):4248.

