“反證法”的一點教學困惑與釋疑*
安徽省阜陽市第二中學 (236000) 劉蘭梅
合肥工業大學附屬中學 (230009) 王 峰
一、問題提出

由此看出,反證法的證題依據是根據邏輯性中的排中律與矛盾律,通過“否定命題結論的反面,從而知原命題的結論正確”,其實質上是駁倒結論的反面,從而反襯出原命題的結論正確,故稱反證法屬于間接證法.
在多年的教學實踐中,筆者一直有個困惑,那就是在運用反證法處理問題中,從“反設(假設結論的否定正確)”出發進行推理論證,導出矛盾,此時我們就說“反設”錯誤,究竟為何呢?即由“矛盾”怎么就知道一定是由于“反設”造成的呢?其依據的原理是什么?有的教師認為反證法實質上是改正原問題的逆否問題,但反證法證題過程中時,從兩個不同角度進行論證,出現“自相矛盾”的現象顯然不是證原問題的逆否問題,故知反證法的本質是改證其逆否命題的說法不完全正確,那么由“矛盾斷定反設錯誤”這一理論依據是什么呢?
二、問題解決
眾所周知,在運用反證法處理問題時,出現的矛盾的情形概括起來無外乎三種情況:一是與數學知識或常識性知識矛盾;二是與題設條件矛盾;三是自相矛盾.事實上,由于出現矛盾的情形不同,則其由“矛盾”斷定“‘假設’是錯誤的”的原理也有所不同,要因“法”而已,下面就根據“矛盾”這三種情形詮釋一下它們判斷“反設錯誤”的依據.
(1)當所證的命題是一個“簡單命題時”時,這樣的命題若用反證法論證時,出現的就是與“常識性知識或題設條件”的矛盾.這種情況的邏輯基礎是原命題與其逆否命題的等價性.
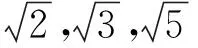
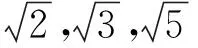
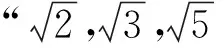


(2)當所證明的命題是“若‘p且q’,則r”時,這種形式的命題若用反證法論證時,我們常常論證命題“r且p?q”或“r且q?p”成立,其推理模式是邏輯學中的反三段論,反三段論的前提“如果p且q,那么r”,可以看作一個三段論,反三段論的結論是“如果p并且非r,那么非q”可以看作是把該三段論的一個前提加以否定,結論也加以否定,并且也調換它們的位置而成.反三段論不但前提蘊含結論,而且結論也蘊含前提,也就是說,前提與結論是等值的.
反三段論的形式是:如果p且q,那么r,所以如果(p并且非r),那么非q.(或如果(q并且非r),那么非p).這個推理形式的有效性可以這樣來解釋:如果同時具備p,q兩個條件,那么就必然出現結果r;當條件p已經具備而結果r沒出現時.就可以推斷另一條件q沒有具備.如零點存在性定理:若函數f(x)在區間[a,b]上連續,且f(a)f(b)<0,則f(x)在區間(a,b)上至少有一個零點.這個定理的條件有兩個:(1)函數f(x)連續;(2)f(a)f(b)<0,結論是“f(x)在區間(a,b)上至少有一個零點”.“假設f(x)在區間(a,b)上沒有一個零點且函數f(x)在[a,b]上連續,則f(a)f(b)≥0.”或“假設f(x)在區間(a,b)上沒有一個零點且f(a)f(b)<0,則函數f(x)在[a,b]不連續.”
由此看出,反三段論的本質是在題設條件有兩個時,即“如果p且q,那么r,”將一個條件p保持不變的情況下,反證法論證的命題是“若非r,則q”,這就是原命題在條件p不變的情況下,命題“若q,則r”的逆否命題,故根據原命題與其逆否命題的等價性,由于反三段論命題:將一個條件p保持不變的情況下,“若非r,則q”是正確的,故知故知原命題在條件p不變的情況下,命題“若q,則r”是真的.反三段論在思維中上經常用到的,如果幾個條件聯合起來構成某一情況的充分條件,那么當該情況不出現時,就可推出幾個條件中至少有一個條件不具備,凡是作這樣的推理時,我們就是應用了反三段論的形式.
案例3函數f(x)在R上是遞增的,且f(a)+f(b)≥f(-a)+f(-b),則a+b≥0.
證明:假設a+b<0,則a<-b,b<-a,因為函數f(x)在R上是遞增的,所以f(a)>f(-b),f(b)>f(-b),兩式相加,得f(a)+f(b) 值得注意的是,利用“反三段論式”推理的反證法,也可理解為改證原命題的逆否命題,這與“反三段論式”的理解是如出一轍,本質一樣.因為當命題的條件和結論不止一個時,原命題的逆否命題不是唯一的,且逆否命題含有原命題的部分條件,這將有助于應用反證法時采用不同的推理方法.例如,“若a,b都是正數,則ab是正數”為原命題,則“若ab不是正數且a正,則b不是正數”、“若ab不是正數且b正,則a不是正數”,它們都是原命題的逆否命題,故與原命題都是等價的.如案例3中,“若函數f(x)在R上是遞增的,且a+b<0,則f(a)+f(b) (3)當用反證法論證時,將結論的反面與題設所有條件都參與使用時,就會出現自相矛盾的現象,這種情形的推理模式是邏輯學中的歸謬式推理.歸謬式推理是根據某一判斷蘊含著兩個不可同真的結果,推出該判斷為假的推理.歸謬式推理的一般形式是: 如果P,那么Q 如果P,那么Q 所以非P 這個推理形式的意思是:如果從一個假定能夠合乎邏輯地導出互相矛盾的結果來,則原來的假定不成立. 在這個推理模式中,為什么由“如果P,那么Q與 如果P,那么Q”就可知命題P是錯誤的呢?其原理是什么呢?因為“如果P,那么Q”?“若Q,則P”,又“如果P,那么Q”,故由“P?Q?P”,顯然這樣的命題P不存在,即非P. 特別指出的是,在利用反證法論證命題是,命題P是指“題設條件+反設”.如不妨設欲論證的命題為“若p,則q”,若用反證法論證命題“若p,則q”時.假設q成立,即將q作為已知條件,如再聯手題設條件p,若從兩個角度進行推理,導出r與r得矛盾出現,就屬于歸謬式推理,因為運用反證法論證時,若將p與q作為推證的條件,此時記“p與q”為P,則若由P既可推出r,又可推出r,根據歸謬式推理知,命題P錯誤,即“p與q”錯誤,說明“p與q”至少有一個錯誤,而命題p是題設條件為真,故知q必錯,根據矛盾律與排中律,知q必正確. 證明:假設a,b,c都不大于0,即a≤0,b≤0,c≤0,則a+b+c≤0;又a+b+c=(x-1)2+(y-1)2+(z-1)2+π-3≥0,這與a+b+c≤0矛盾,故假設錯誤,所以a,b,c中至少有一個大于0. 當然,究竟推證的“矛盾”究竟使用三類中的哪一類,與論證過程的表達方式有關,如案例2,運用反證法也可這樣表達過程: 對于反證法的學習,常常表現為學生問教師:“反證法這一內容高考考不考?”從這個問法就可看出學生對于“反證法”的學習容易產生誤解,認為學習反證法就是為了做題,實則時是對反證法的學習價值的認識不到位,的確,表面上,多年來高考試題沒有明顯呈現“反證法”的題目,但是運用反證法解題的思想無不是不知不覺中在使用. 例如在解答選擇題時,我們為了判斷某個選擇支是否正確,不妨設A選項,若直接不易判斷A是否正確,我們常常假設這個選擇支A正確,如果結合題設條件進行推理,不出現矛盾,就認為A正確;如果結合題設條件進行推理,出現了矛盾,就認為A錯誤,這一錯誤判斷的過程,其實就是使用了反證法的“反證思想”. 又如,舉反例也是我們駁倒某個命題的常用方法,其實質上就是反證法的運用.特別是,當提出一個命題之后,就面臨兩種選擇:一是推證命題成立;二是尋找一個滿足命題的條件使結論不成立,從而否定這個命題,這就是舉反例. 事實上,舉反例是一種重要的反證手段,故學會構造反例也是一種重要數學技能,應該成為數學教學的基本內容而滲透于教學過程之中,所以學習反證法的意義重大,但為什么經常使用“反證法”的思想解題,而沒有意識到在使用反證法呢?筆者認為根本原因是沒有理解透反證法的原理所致,將反證法的三個步驟只是死記硬背的結果,解題時機械操作過程罷了,之所以出現這種現象,筆者認為教師在教授“反證法”時,推理講的多,而對“反證法”的原理分析的少,結果導致學生知其然而不知所以然,很大程度上是我們教學中沒有講清楚根源,不清楚的講解,學生沒消化,不能做到融會貫通.本文給大家關于“反證法”的一個困惑解釋一下,相信對大家有一定的幫助.
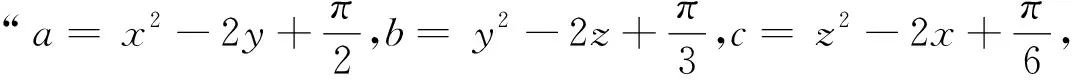
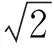
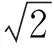


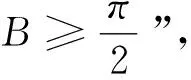
三、教學思考

