2023年新高考全國Ⅱ卷21題的解法與溯源

重慶市綦江中學 (401420) 晏炳剛 劉 燕

2023年新高考全國Ⅱ卷21題是一道定點定直線的問題,涉及非對稱韋達定理的處理,也關聯極點極線背景問題.本文就該題解法進行分析,先給出多種非對稱韋達定理處理思路,再對雙曲線背景題目進行溯源,得到更一般性的結論,最后把結論推廣到橢圓中.

1.題目呈現

⑴求曲線C的方程;

⑵記C的左右頂點為A1,A2,過T(-4,0)的直線l與C 交于M,N兩點,點M在第二象限,記MA1,NA2的交點為P,證明:點P在定直線上.

2.解法探究

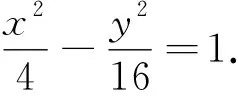
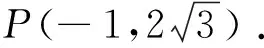
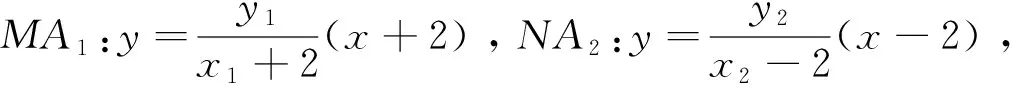
⑶是非對稱形式的韋達定理,下面是處理方法.

思路1 部分韋達定理+消元化簡

思路2 構造韋達定理消元化簡

思路3 韋達定理積化和

思路4 韋達定理和化積

思路5 代入曲線構造韋達定理

思路6 方程組法

y2x1+y1x2=k(x2+4)x1+k(x1+4)x2

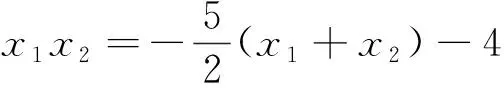
點評：此解法是消去y,留下x的解法.核心思路是求交點P的軌跡方程,聯立直線方程求交點坐標是基本思路,進而得到

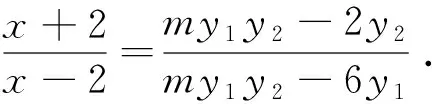
以上6個處理方法,思路1和2,計算量適中.方法3和4,計算量小.方法5構造對稱式意義較大,方法6思路巧妙.

3. 題目溯源

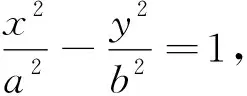
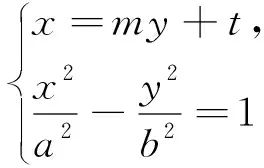
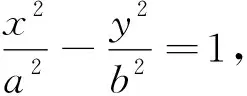
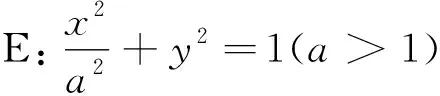
(1)求E方程;(2)證明:直線CD過定點.