例析幾道競賽組合題的解法

江西科技學院附屬中學 (330000) 閔書存

江西省南昌市新建第一中學 (330103) 閔幼梅

組合數學中基本的問題之一是組合計數問題,這部分內容在高中數學中通過排列與組合這一章節進行考察,解決組合計數問題需要學生熟練使用常見的組合計數模型,能夠靈活地設計分類與分步方法,充分利用對稱思想,靈活地將計數問題進行轉化,適當地使用正難則反的思想,建立m對n的對應關系等.本文以近年高中數學聯賽一試中的組合計數問題為例,剖析其解答過程歸納組合計數問題常見的幾種解答方法.

例1 在5×5矩陣中,每個元素都為0或1,且滿足:五行的元素之和都相等,但五列的元素之和兩兩不等,這樣的矩陣個數為________.(2022年全國中學生數學奧林匹克競賽預賽A1卷第8題)

分析1：本題要求五列的元素之和兩兩不等,考慮到一列的和只能取0-5這六種情況,因此五列的列和是0、1、2、3、4、5這些數字中的5個,又考慮到五行的行和都相等,故矩陣中所有元素之和是5的倍數,經過這樣的分析,我們得到五列的列和只能是0、1、2、3、4或者1、2、3、4、5這兩種情況.

分析2：事實上,我們可以建立五列的列和是0、1、2、3、4這種情況和五列的列和是1、2、3、4、5這種情況的一一對應關系,只需將五列的列和是0、1、2、3、4這種情況中列和為0這一列全部填上1則唯一地對應成五列的列和是1、2、3、4、5這種情況.反之,將五列的列和為1、2、3、4、5這種情況中的列和為5這一列全部換成0,則唯一地對應成五列的列和是0、1、2、3、4這種情況,這表明兩種情況的計數數量相同,因此只需計算其中一種情況的計數數量即可.

分析3：考慮列和為1、2、3、4、5的情況的填數方法數,利用對稱性,五列的列和的排布方式總數量5!中的每一種對后續填數方法計數影響一致,故只需考慮圖1中從左到右的列和順序為1、2、3、4、5的情況.

分析4：又由于第一列的1放置在哪一行對后續計數影響一致,第5列已經全部填寫了1,故只需考慮第1列的1放置在第一行的情形,此時的表格簡化為只需考慮如圖2所示的5×3的表格.

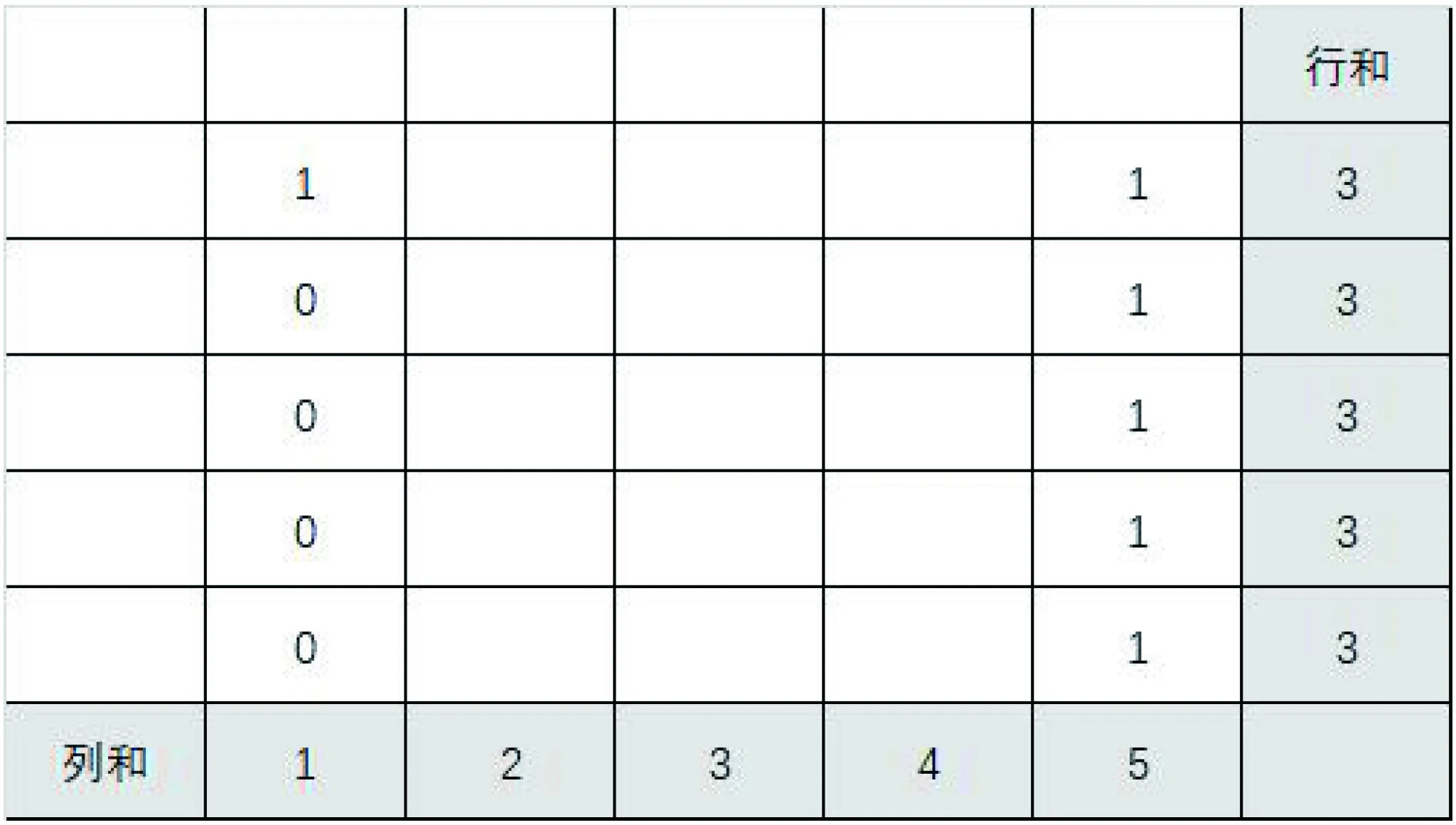
圖2

分析5：考慮第四列的0應當放置在何處,可以分為兩類,一類是0被放置在第一行,一類是0被放置在第二、三、四或者五行,后一類的四種情況對后續計數產生的影響一致,因此只需考慮其中一種情況即可.根據行和為3,部分位置的元素已經被確定,故接下來只需對以下圖3、圖4兩種情況進行計數:

圖3

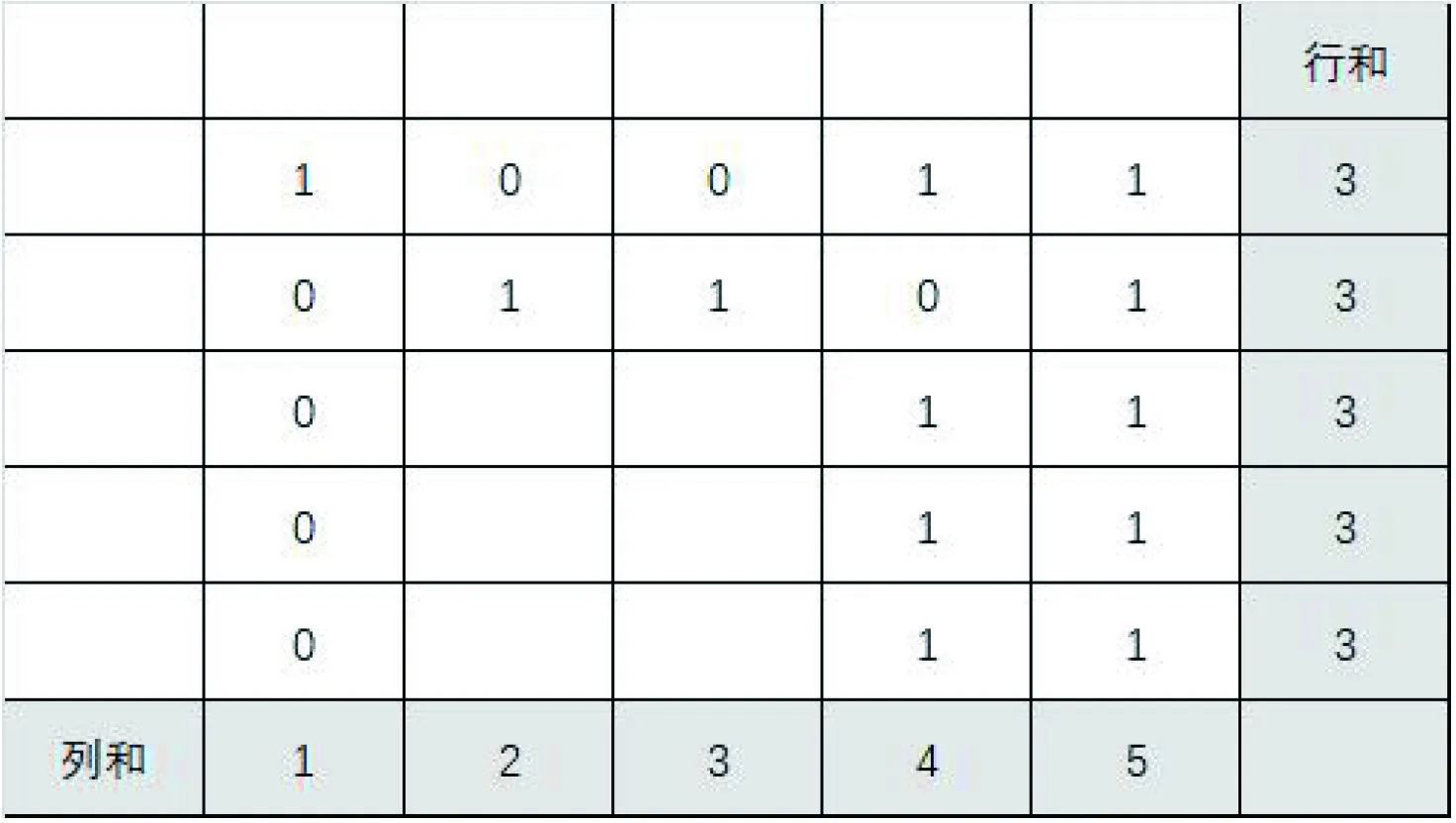
圖4

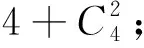
點評：在本題的分析過程中,不斷地通過對稱思想簡化要填寫的表格,最后通過合理的分類與分步將問題解決,充分體現了對稱思想在處理組合計數問題中的作用.

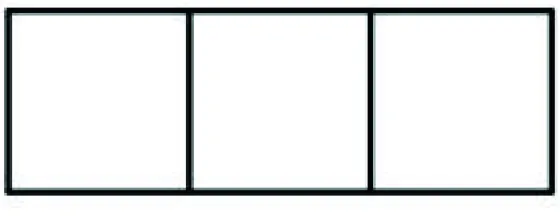
圖5

例一個單位方格的四條邊中，若有兩條邊染了顏色i，另兩條邊分別染了異于i色的另兩種不同顏色，則稱該單位方格是i色主導”的.如圖)5，一個1×3方格表的表格線共含10條單位長線段，現要對這10條線段染色，每條線段染為紅、黃、藍三色之一，使得紅色主導、黃色主導、藍色主導的單位方格各有一個，這樣的染色方式數為_________.(2022年全國中學生數學奧林匹克競賽預賽A卷第8題)

分析1：為方便說明,我們對邊進行如下的編號為如圖6:

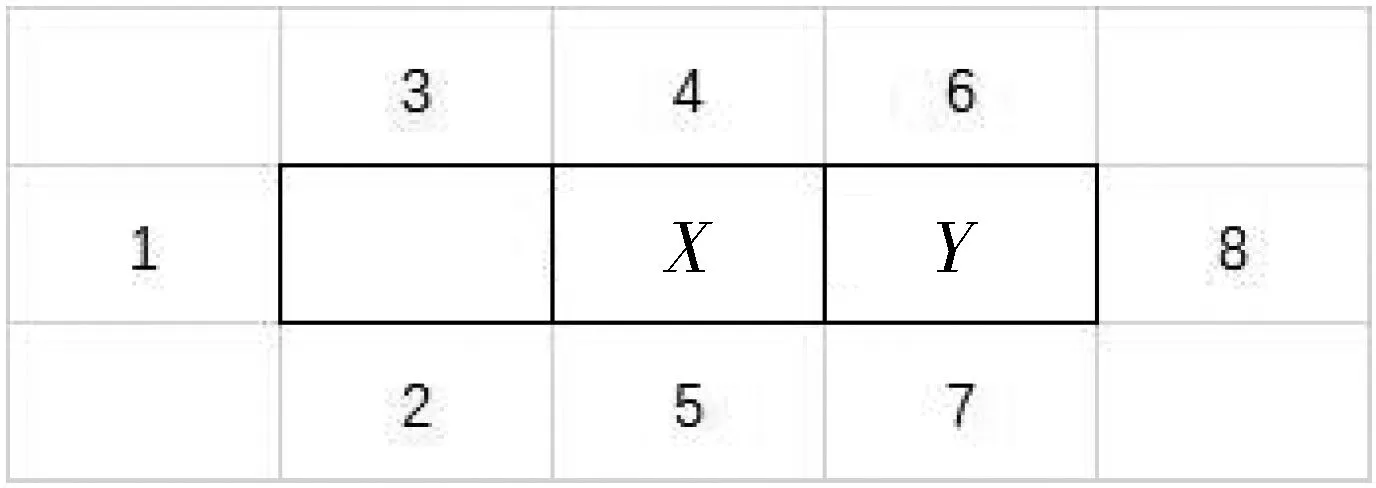
圖6

由對稱性,三個主導顏色的排列順序對后續計數的影響是相同的,因此,只需考慮從左至右三個主導顏色的排列順序為紅黃藍的情況.

分析2：觀察10條邊的特征,發現這些單位方格中的兩條公共邊最特殊,它們中的每一個都會對兩個方格的染色方式產生影響,因此從對象的這一特征入手進行分類.考慮到中間的方格是黃色主導,因此,這兩條公共邊的顏色可以同時是黃色或者其中之一為黃色,或者二者均不為黃色.下面對這三種情況分別進行計數.

分析3：如果XY這兩天邊均為黃色,則邊45可任意染成紅色和藍色即可,故方法數為2;由對稱性,邊123的染色方法數與邊678的染色方法數相等.故只需考慮邊123的染色方法數,只需確定藍色邊的位置即可,故方法數為3.綜合可得此種情況下,染色方法數為2×3×3=18.

分析4：如果XY這兩邊其中之一為黃色,有三種情況需要考慮,分別是X和Y為黃色和紅色、X和Y為黃色和藍色、X和Y為紅色和黃色、X和Y為藍色和黃色,其中X和Y為黃色和紅色這種情況與X和Y為藍色和黃色這種情況具有對稱性,X和Y為紅色和黃色這種情況與X和Y為黃色和藍色這種情況具有對稱性,下面又分別考慮它們.

分析5：若X和Y為黃色和紅色,則45應為黃藍或者藍黃,故染色方法數為2;123應當有兩邊為紅,一邊為藍,故染色方法數為3.678應當由兩邊為藍,一邊為黃,故染色方法數為3;故這種情況下的染色方法數為2×3×3=18.

分析6：若X和Y為紅色和黃色,則45應當有一邊為黃,一邊為藍,故染色方法數為2;123應當是三個顏色,故染色方法數為3!=6;678應當有兩邊為藍,一邊為紅,故染色方法數為3;故這種情況下的染色方法數為2×6×3=36.

分析7：如果XY這兩邊均不為黃色,則45必須均為黃色,此時有兩種情況需要考慮,一種是XY為紅色和藍色,一種是XY為藍色和紅色;若XY分別是紅色和藍色,則123應當是三種顏色,故染色方法數為3!=6;678應當也是三種顏色,故染色方法數為3!=6,故總的染色方法數為6×6=36;若XY分別是藍色和紅色,則123應當有兩邊為紅色一邊為黃色,故染色方法數為3;678應當有兩邊為藍色一邊為黃色,故染色方法數為3,總的染色方法數為3×3=9.

綜上分析可知,總的染色方法數為((36+9)+(36+18)×2+18)×3!=1026.

點評：解決該問題需要靈活地設計分類與分步方法,同時要充分利用對稱思想減少復雜度.

例3 將6個數2,0,1,9,20,19按任意次序排成一行,拼成一個8位數(首位不為0),則產生的不同的8位數的個數為________.(2019年全國中學生數學奧林匹克競賽預賽A卷第8題)

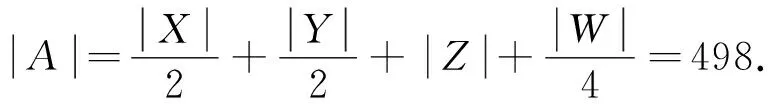
點評：本題通過構造兩個集合的元素之間的映射關系,巧妙地解決了求解其中一個集合的元素的個數的問題,這種方法是解決組合計數問題的常見方法之一.

以上三道試題的剖析,演示了全國高中數學聯賽的組合計數問題中幾種常見的解答方法和解答思想,總體上,解決組合計數問題可以歸納為如下思路:(1)在理解問題的基礎上將問題的主要特征提取出來;(2)考慮是否需要對問題進行適當轉換;(3)根據提取的特征設置適當的分類與分步方式;(4)充分地利用對稱思想減少討論的情況數;(4)在細節處理上適當地使用正難則反的思想;(5)部分不方便計數的問題可以考慮建立集合與集合之間的映射關系.