考慮沖擊與齒根應力的齒輪接觸穩定性分析

何延曉，王承登，伍宏建，劉威，劉鵬

(重慶交通大學機電與車輛工程學院，重慶 400074)

0 前言

漸開線圓柱齒輪傳動作為主要的傳動方式之一，廣泛應用于航空航天、船舶海洋、交通運輸等重要行業。接觸穩定性是評價齒輪傳動品質的關鍵指標，穩定性低的齒輪系統會導致齒輪使用壽命降低、安全可靠性差、各激勵耦合作用明顯、振動噪聲顯著等問題。因此，對齒輪系統接觸穩定性展開研究具有重大理論意義及工程應用價值。

現已有大量學者對齒輪系統嚙合特性展開研究[1-3]。部分學者為探究齒輪接觸特性，對其接觸狀態進行了以下分析：梁棟等人[4]推導了齒輪空間共軛曲線副嚙合方程，對接觸跡線進行了計算與分析；段文浩等[5]研究了不同螺旋角下雙圓弧齒輪的嚙合特性，分析了螺旋角對嚙合特性的影響；王羽達等[6]考慮齒間分配載荷，對齒輪進行了承載接觸分析。

為探尋齒輪穩定性的影響因素及其貢獻度，部分學者對不同物理量與激勵進行分析，研究其對接觸特性的影響。劉明勇等[7]應用有限元法分析了斜齒輪的塑性變形、材料線性強化、溫度及摩擦等因素對齒輪嚙合特性的影響，并用實驗進行驗證；萬志國等[8]建立齒輪系統動力學模型，研究了齒側間隙、時變剛度、嚙合阻尼對齒輪系統動力學特性的影響；陳安華等[9]建立了動力學模型，探究了嚙合阻尼、支承阻尼、重合度與支承剛度對齒輪系統動力穩定性的影響；曲偉等人[10]分析了不同轉速與負載下減速器齒輪的變形量與最大等效應力的變化，并得出相應的變化規律。

綜上可知，關于齒輪接觸特性以及嚙合穩定性的研究眾多，且已取得一定的研究成果。大多學者均是對各因素進行單獨影響分析，缺少對不同工況下嚙合沖擊、齒根應力等各因素間的演變耦合規律進行分析。因此，本文作者以一對機匣齒輪為分析對象，應用能量守恒定理計算不同工況下齒輪嚙合沖擊，應用修改后齒根應力算法計算不同轉矩下的危險截面齒根應力，然后通過有限元法計算實際工況下齒輪動態接觸力，并與理論值對比，驗證其可靠性。探究不同工況下齒輪接觸力穩定性情況，結合嚙合沖擊與齒根應力，綜合分析其影響關系，得出齒輪接觸穩定性受轉速、轉矩、嚙合沖擊、齒根應力的影響規律，為齒輪系統最佳工況選取及接觸穩定性優化提供參考。

1 理論方法

1.1 嚙入沖擊理論

嚙合沖擊包括嚙入沖擊與嚙出沖擊，由于嚙入沖擊影響遠遠大于嚙出沖擊，因此主要針對嚙入沖擊進行分析。

理想狀態下，主被動齒輪基圓齒距相等，齒對沿嚙合線正常嚙合，但由于齒廓誤差與輪齒受載變形等因素影響，齒距發生微量變化，主從動基圓齒距不等，嚙入點偏離嚙合線致使線外嚙合。而未在嚙合線內正常嚙合齒對沿瞬時嚙合線方向速度不等，產生沖擊速度，導致嚙入沖擊。如圖1所示，Pb1與Pb2分別為主從動輪瞬時齒距、嚙入產生的相對齒距差ΔPb導致點A線外嚙合，出現沖擊速度vs，嚙入沖擊在點A產生。

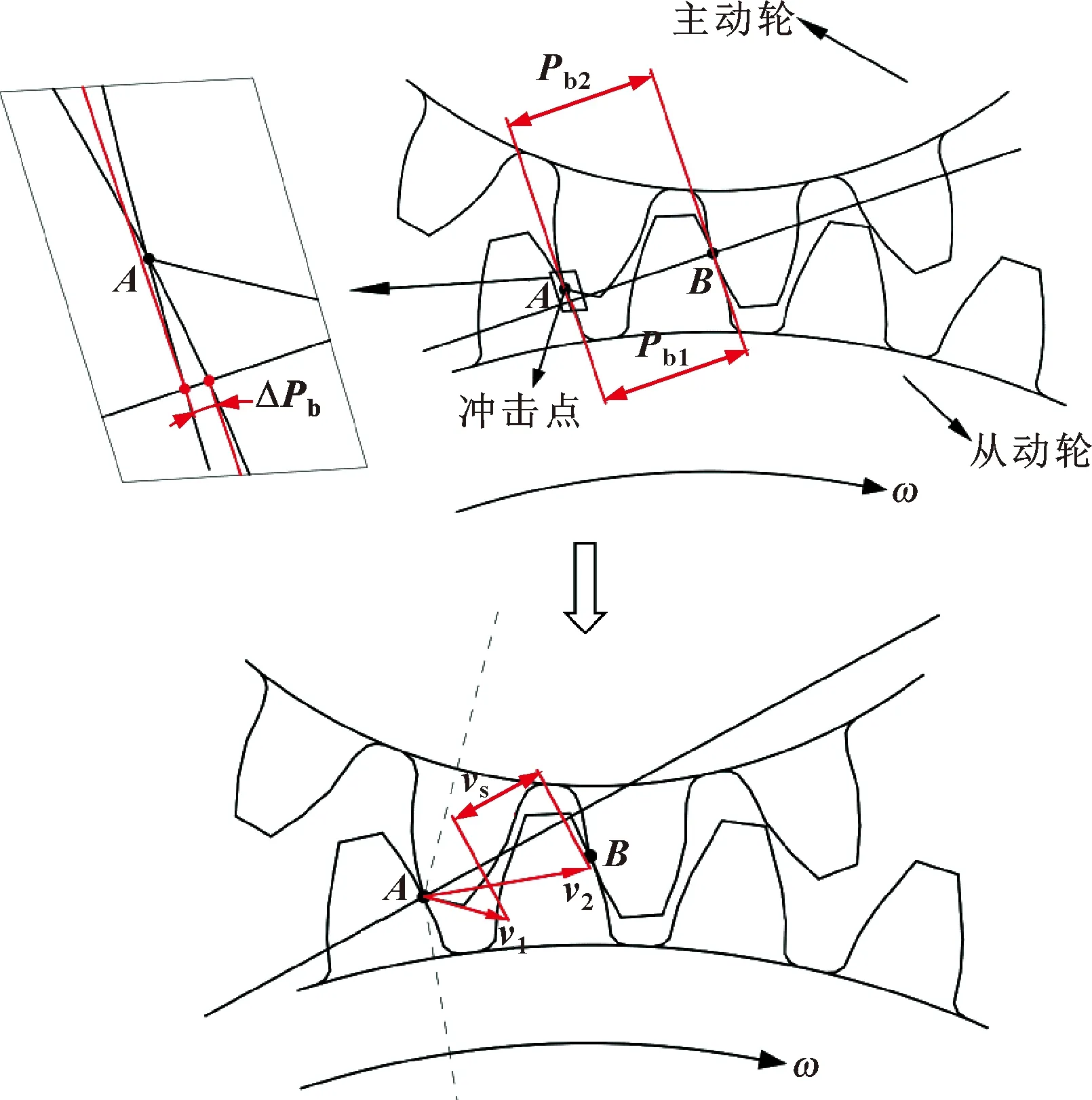
圖1 嚙入沖擊示意

首先確定沖擊點位置，應用反轉法得到嚙入沖擊點幾何位置圖，如圖2所示。幾何間隙角φ可由變形量求得：

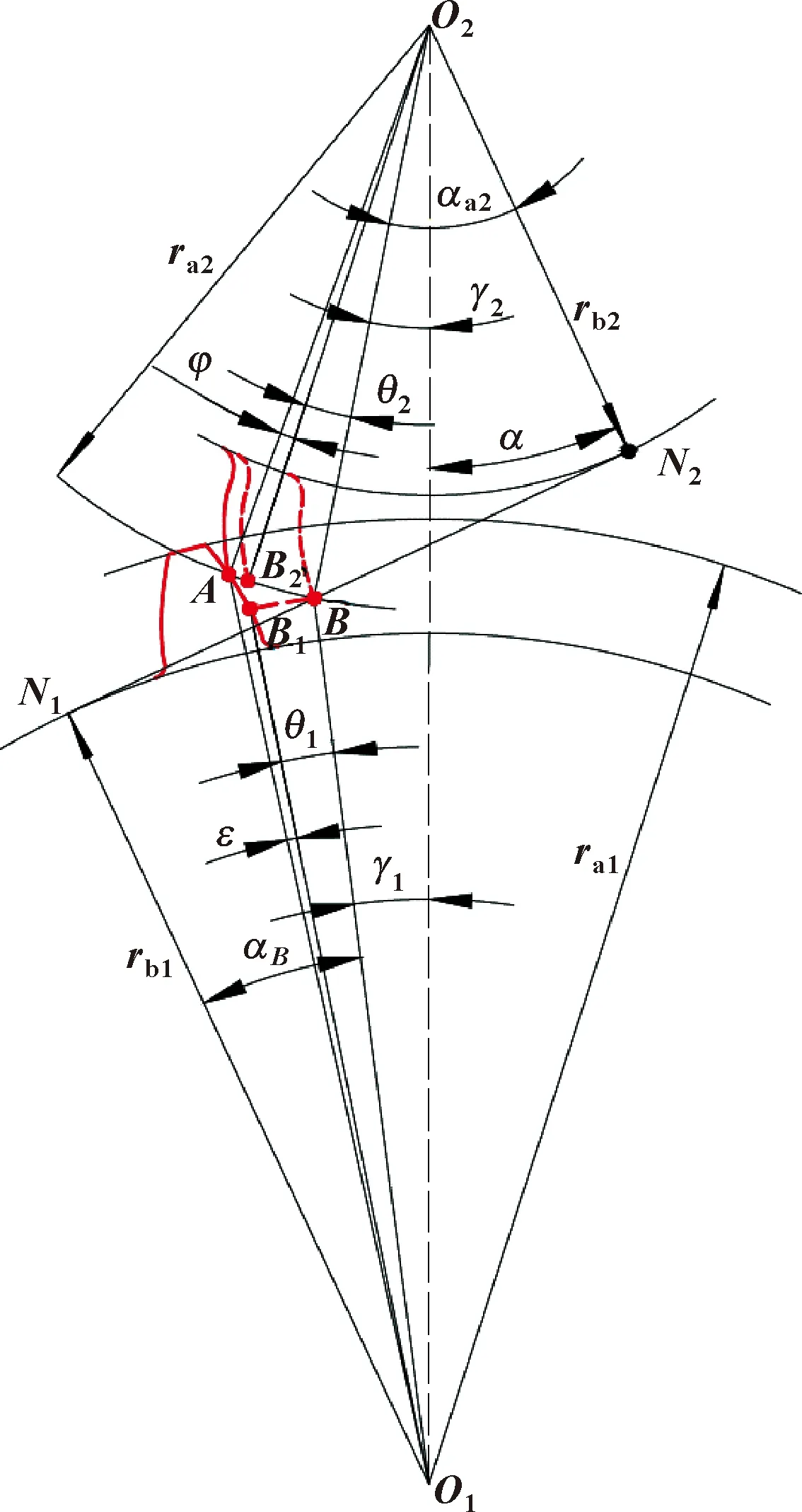
圖2 沖擊點幾何位置

φ=δΣ/rb2

(1)

δΣ=δ1+δ2+δc

(2)

式中：δΣ為前一齒對沿嚙合方向總變形量；δc為前一齒對齒面接觸變形量；δ1、δ2為前一齒對沿嚙合方向產生的撓曲變形量。

由幾何關系可得：

(3)

(4)

(5)

γ1=α-αB

(6)

γ2=αa2-α

(7)

ε=invαA-invαB

(8)

式中：αB為理論嚙合點B的壓力角；k為傳動比；a為中心距；rO1A為沖擊半徑；α為齒輪副壓力角；θ1、θ2為主從動輪反轉角度；αA為沖擊點壓力角；ε為主動齒上提前嚙入角度；αa2從動輪齒頂圓壓力角；ra2為從動輪齒頂圓半徑；γ1、γ2位置如圖2所示。

聯立式(1)—式(8)可求解沖擊半徑，即確定了沖擊位置。在沖擊瞬時可做如圖3所示等效瞬時基圓與嚙合線，則嚙入沖擊速度vs為

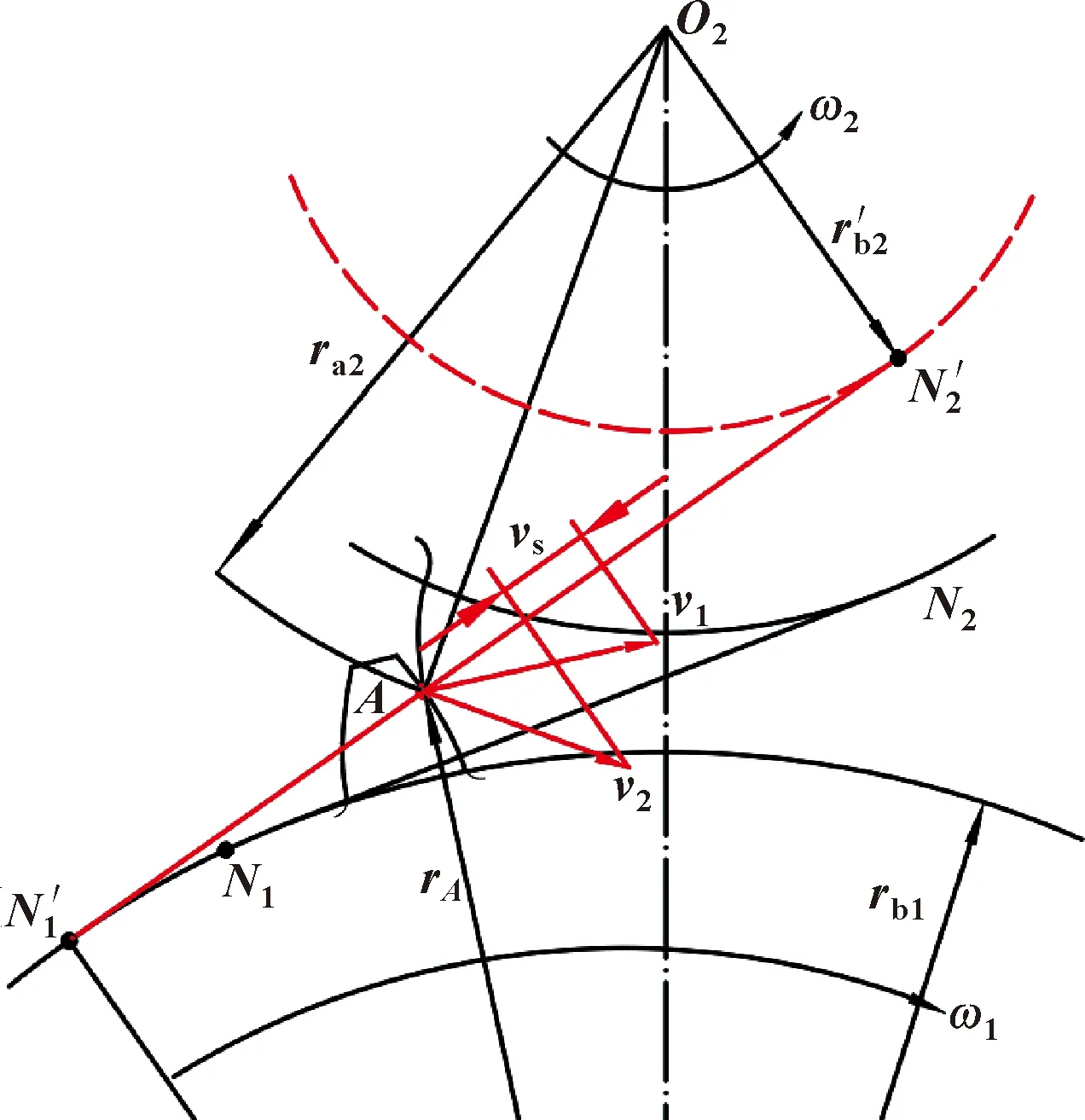
圖3 等效基圓

(9)

(10)

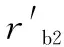
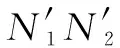
(11)

(12)

式中：m1、m2分別為主、從動輪在瞬時嚙合線上的誘導質量；J1、J2分別為主、從動輪的轉動慣量；rh1、rh2分別為主、從動輪輪轂內孔半徑；ρ為密度；b為齒寬。

根據沖擊力學理論，每片直齒輪副之間產生的最大變形量δs、最大沖擊力F及沖擊能量Ek之間的關系可以表述為

(13)

式中：qs為齒輪副嚙入沖擊點的綜合柔度，qs=q1+q2+qh，q1、q2分別為主、從動輪齒在嚙入沖擊點處的彎曲變形柔度，qh為輪齒在嚙入沖擊點處的接觸柔度。

由式(13)可求齒輪副最大沖擊力的表達式：

(14)

1.2 齒根應力計算方法

目前齒輪齒根應力主要應用漸開線圓柱齒輪承載能力計算方法GB/T 3480計算，但是對于變壓力角滾刀加工的齒輪，此方法會出現較大偏差。因此，文中應用修正后的齒根彎曲應力計算方法進行求解。

將齒輪加工滾齒運動等效為齒輪固定不動、滾刀繞齒輪做純滾動運動，如圖4所示。

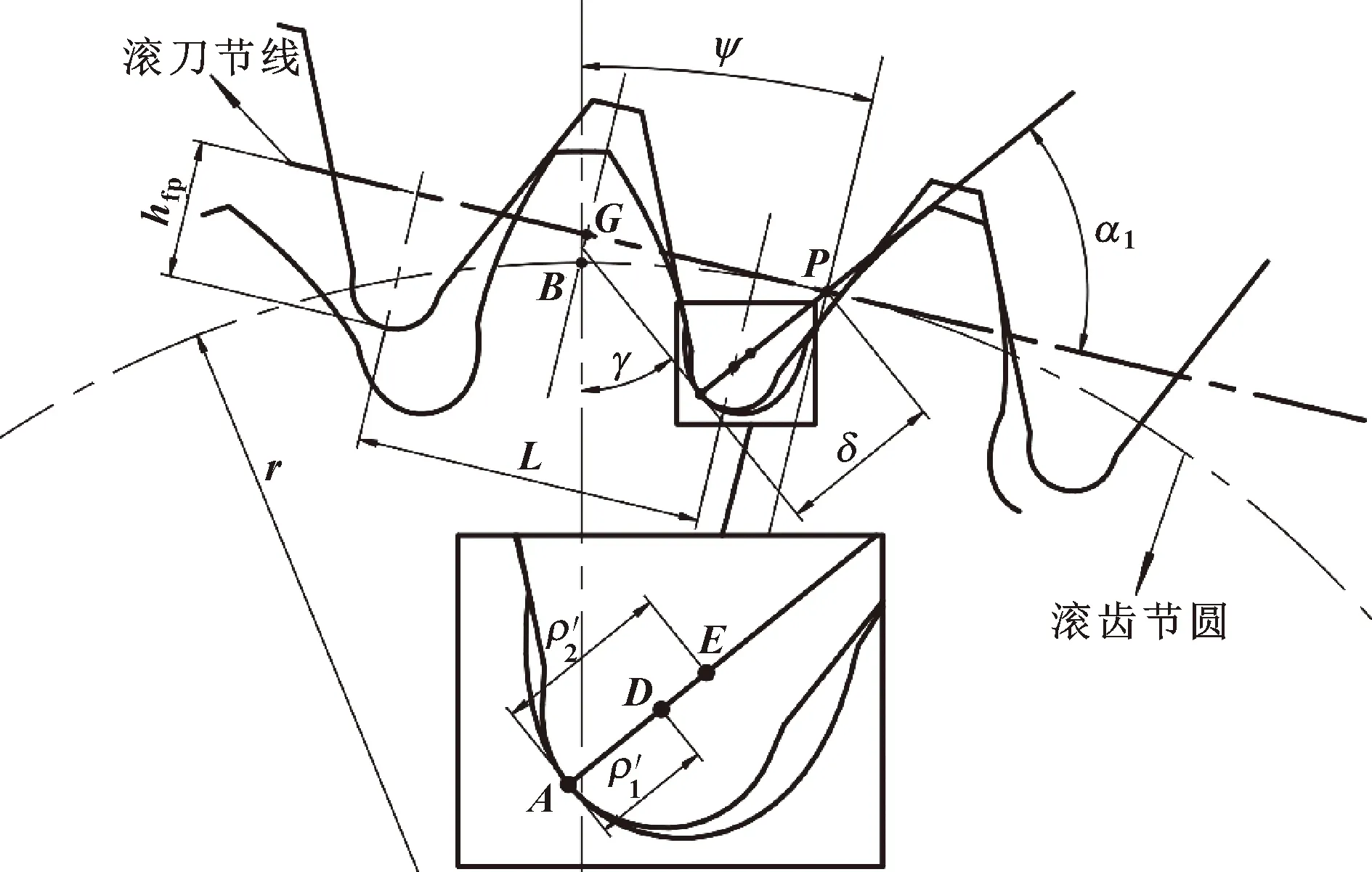
圖4 齒輪與滾刀嚙合示意

圖中，點A為滾刀與齒輪瞬時接觸點，點D為滾刀頂部圓角圓心，AE為齒根接觸點A處曲率半徑，點P為滾刀與齒輪速度瞬心，ψ為P與齒輪中心連線和齒形對稱線間夾角，L為滾刀節距。據滾齒原理可知弧長BP等于GP，因此根據圖中幾何關系得：

r×ψ=L/2+(hfp-ρfp)/tanα1

(15)

γ+ψ=α1

(16)

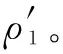
以齒輪圓心為坐標原點建立直角坐標系，則點A的坐標可以表示為

(17)

Euler-Savary公式可以表示共軛曲線與瞬心線曲率半徑的關系，一般形式為

(18)

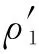
由于兩瞬心線內切，則式(18)中曲率半徑取負值。將此式應用到滾齒運動中，齒根各點的曲率半徑可表示為

(19)

令γ=30°，由式(15)(16)可求解α1，從而求得齒根危險截面處曲率半徑。

圖5所示為輪齒載荷作用示意，αFen為輪齒嚙合外界點載荷作用角，γe為外界點處齒厚半角，圖中點C坐標值可由式(3)求得。由圖中關系可知：

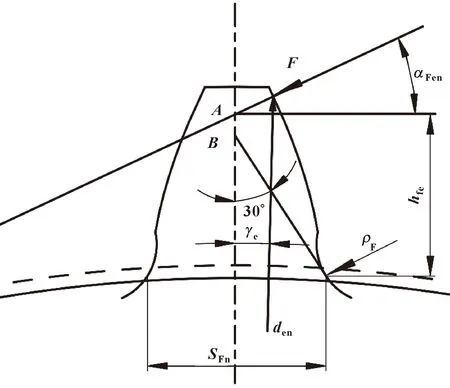
圖5 載荷作用于單對齒嚙合區外界點示意

SFn=2x

(20)

hFe=0.5dencosγe-0.5densinγetanαFen-y

(21)

式中：SFn為危險截面齒厚；hFe為彎曲力臂；den為輪齒嚙合外界點直徑。

應力修正系數Ys與齒形系數YF為

(22)

(23)

式中：L為齒根危險截面齒厚與彎曲力臂比值；qs為齒根圓角參數；α為齒輪分度圓壓力角；m為模數。

至此，經修正的齒輪齒根應力σF可求得：

(24)

σF=σF0KAKvKFβKFα

(25)

式中：σF0為齒根應力的基本值；Yβ為螺旋角系數；Fτ為齒輪分度圓上切向力；KFα為彎曲強度計算的齒間載荷分布系數；KA為使用系數；Kv為動載系數；KFβ為彎曲強度計算的齒向載荷分布系數。

2 接觸力數值計算

齒輪嚙合在考慮摩擦、齒側間隙及齒輪各內部激勵等因素共同作用下為強非線性系統，且各激勵作用下產生的振動響應又反作用于各激勵，造成復雜的多非線性耦合轉化反饋現象。因此，擅長進行幾何非線性分析的有限元法能夠更準確地對此類問題求解，文中用LS-DYNA的顯式直接積分法，進行連續嚙合齒輪動態接觸力求解。

首先建立齒輪嚙合分析精確三維模型，然后對其進行有限元網格離散，得到漸開線直齒輪傳動有限元動態嚙合分析模型如圖6所示。齒輪外部使用Solid164三維實體單元劃分，因Shell63單元具有旋轉自由度，方便工作載荷添加，故齒輪內圈表面選用剛性殼體單元Shell63，實體單元與剛性殼體單元共用節點。為還原真實工況，對齒輪體內孔的所有平動自由度進行了約束，對齒輪除繞軸外的所有轉動自由度進行了約束，在主動齒輪內圈添加驅動轉速，從動齒輪內圈添加負載扭矩，在所有齒對間建立接觸關系。

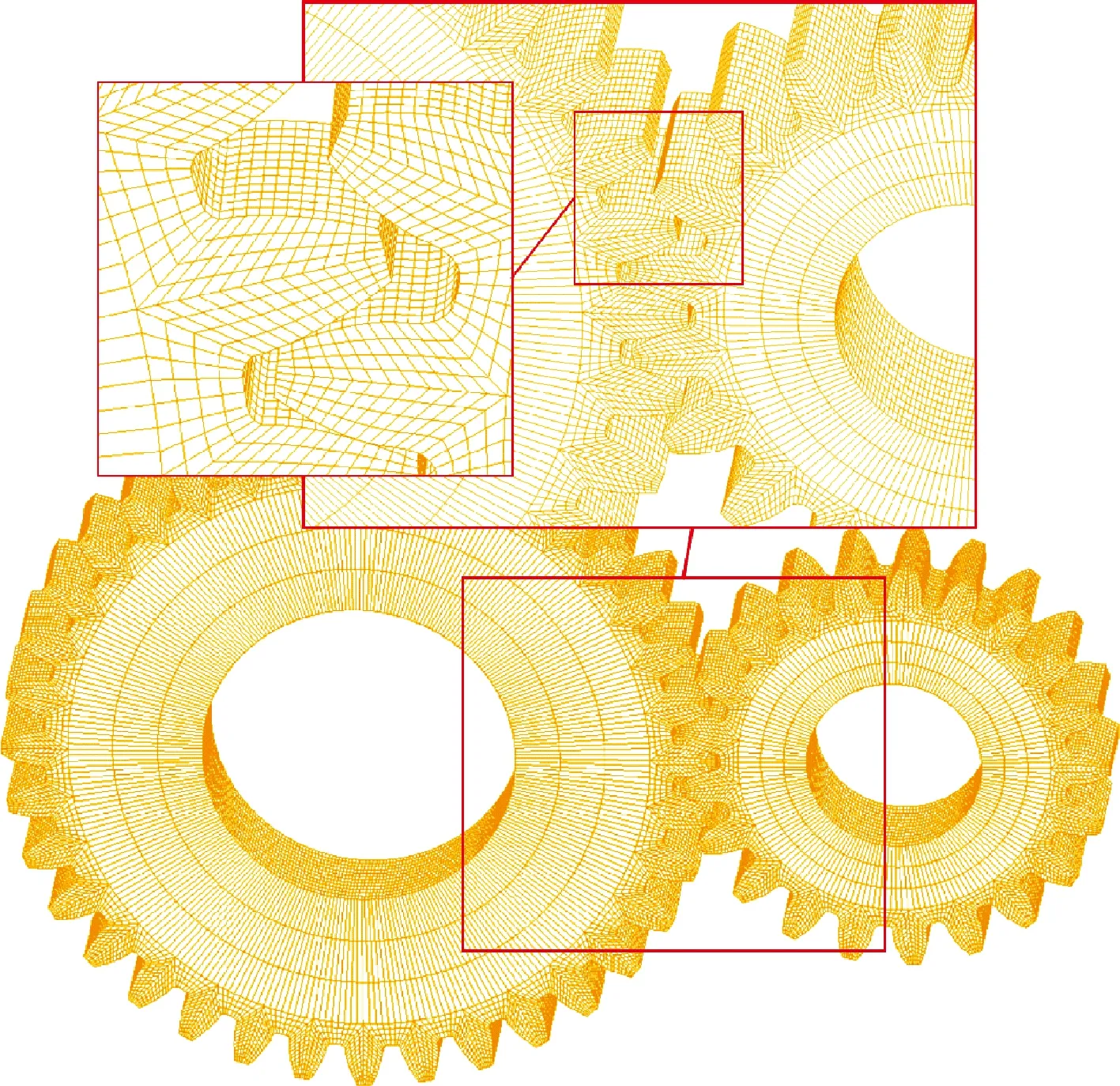
圖6 動態嚙合模型

文中分析對象為一對航空機匣齒輪，齒輪參數如表1所示。為模擬真實啟動狀態，加載過渡時間為3對嚙合齒時間，求解時間設置為主動輪轉動一周時間，此時齒輪嚙合已達相對平穩狀態。以轉矩150 Nm、轉速1 500 r/min為例，載荷歷程曲線如圖7—圖8所示。

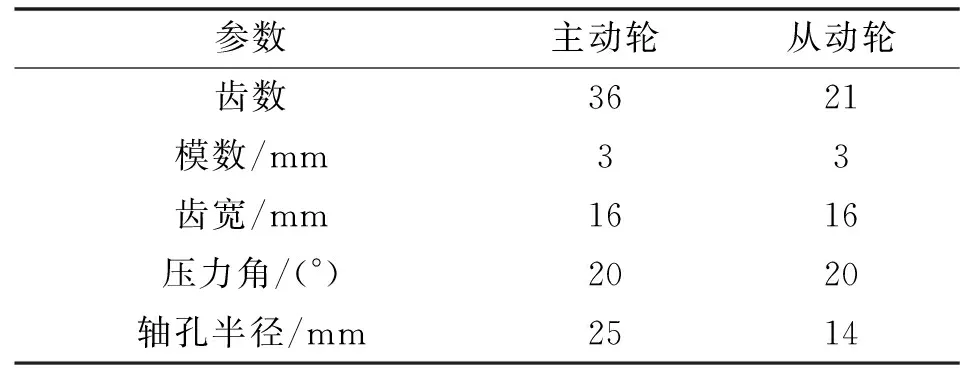
表1 齒輪參數

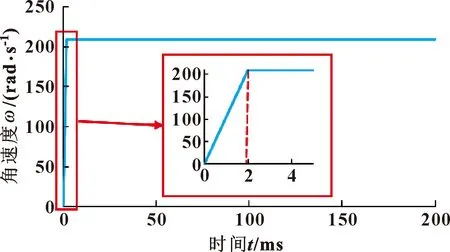
圖7 加載轉速

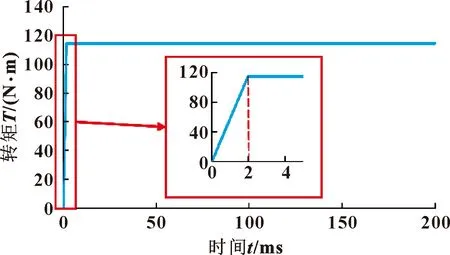
圖8 加載轉矩

求解結束后提取從動輪角速度如圖9所示，可知：2 ms加載結束后，從動輪轉速在理論值269.28 rad/s附近波動，驗證了轉速的合理性。

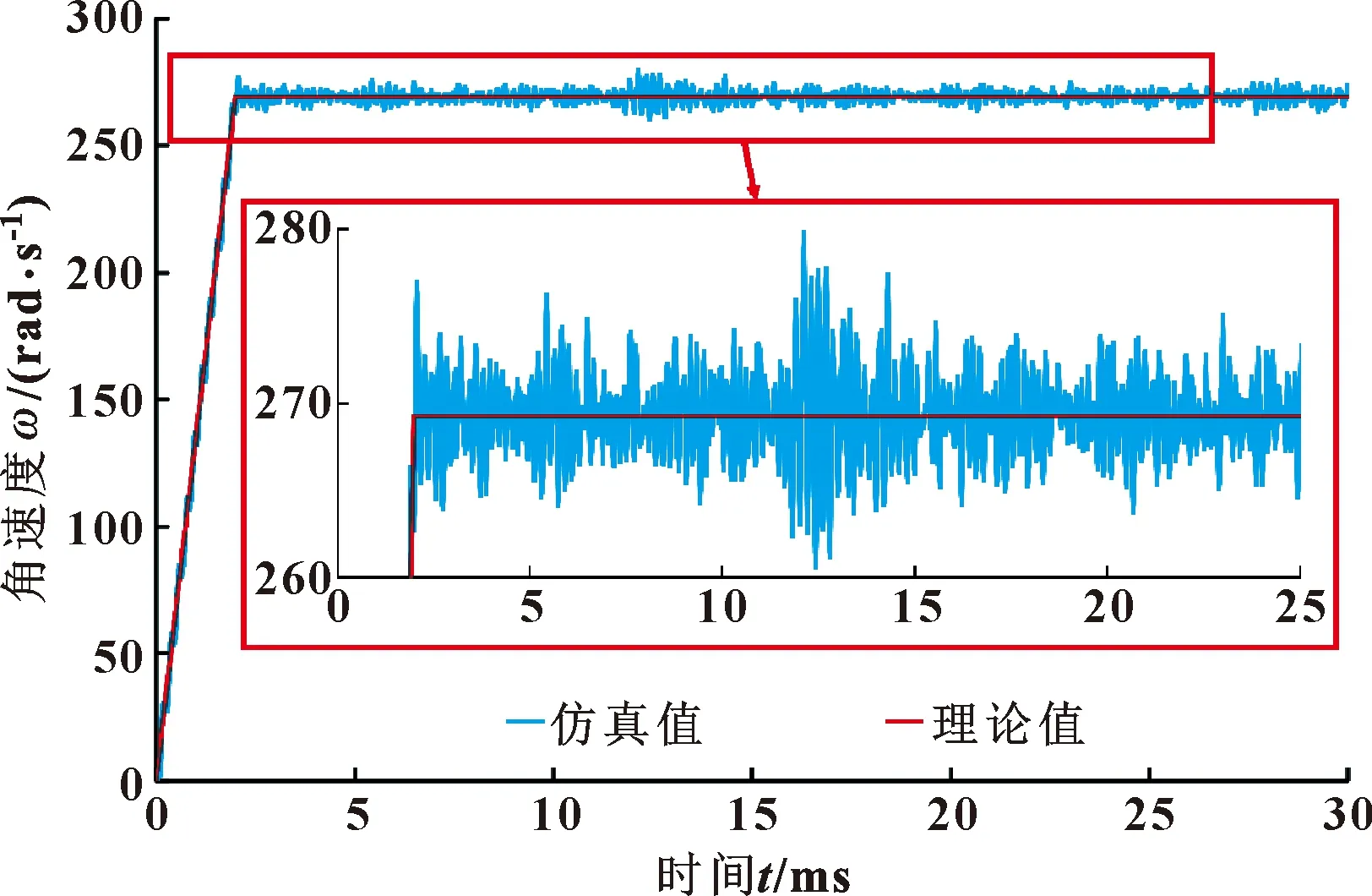
圖9 從動輪動態角速度

提取齒輪穩定運行后齒對動態接觸力如圖10所示，計算得數值計算接觸力平均值為3 031.287 N，與理論解析值2 956.05 N誤差為2.5%，在各激勵耦合作用下，數值解略高于理論值，但誤差在合理范圍內，故該數值解析法合理性得以驗證。

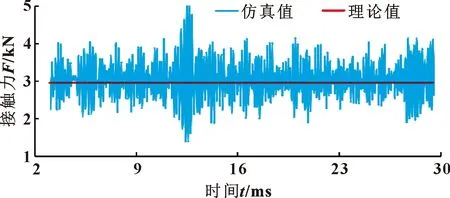
圖10 動態接觸力

3 變工況下齒輪接觸穩定性分析

為揭示不同工況下嚙合沖擊、齒根應力、接觸穩定性間的內在關聯與影響關系，將三者進行對比分析，以便進一步進行最優工況的選取及接觸穩定性優化方法研究。

針對文中研究對象即機匣齒輪設置5個不同轉速，分別為500、1 000、1 500、2 000、2 500 r/min，設置5個不同轉矩分別為50、100、150、200、250 N·m。

將第一節嚙合沖擊與齒根應力計算方法編為MATLAB程序，分別對不同工況下的嚙合沖擊力與齒根應力進行計算，得出如圖11所示的不同工況下兩指標變化規律。

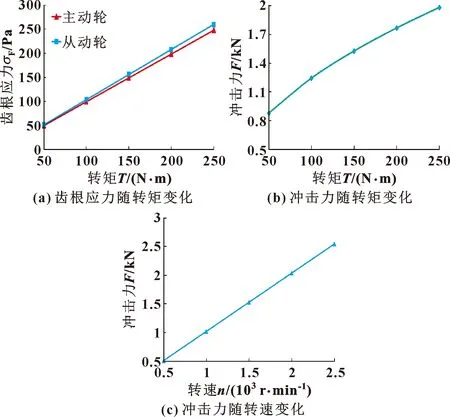
圖11 沖擊力與齒根應力變化規律

圖11(a)中，從動輪齒根應力大于主動輪，且主從動輪的齒根應力均隨轉矩增大而增大。由于轉矩增大導致嚙合力增大，因此齒根應力也隨之增大，由圖11(a)可知應力與轉矩幾乎成正比的關系。

由圖11(b)(c)知，嚙合沖擊力隨轉速與轉矩的增大而增大，且隨轉矩增大，沖擊力的增大趨勢減緩，而沖擊力與轉速幾乎成正比關系增長。結合理論分析，當輸入轉矩增加，齒輪輪齒接觸力增加，導致輪齒受載變形量變大，沖擊速度變大，嚙合沖擊力增大。而轉速增加會導致嚙合沖擊速度增大，因此嚙合沖擊力增加。

在研究工況對接觸穩定性影響時，將轉矩與轉速分為2組進行討論，第一組設置轉速為1 500 r/min，轉矩分別取50～250 N·m；第二組設置轉矩為150 N·m，轉速分別為500～2 500 r/min。第一組變轉矩數值計算時變接觸力如圖12所示，通過接觸力變化幅值與標準差衡量接觸穩定性。

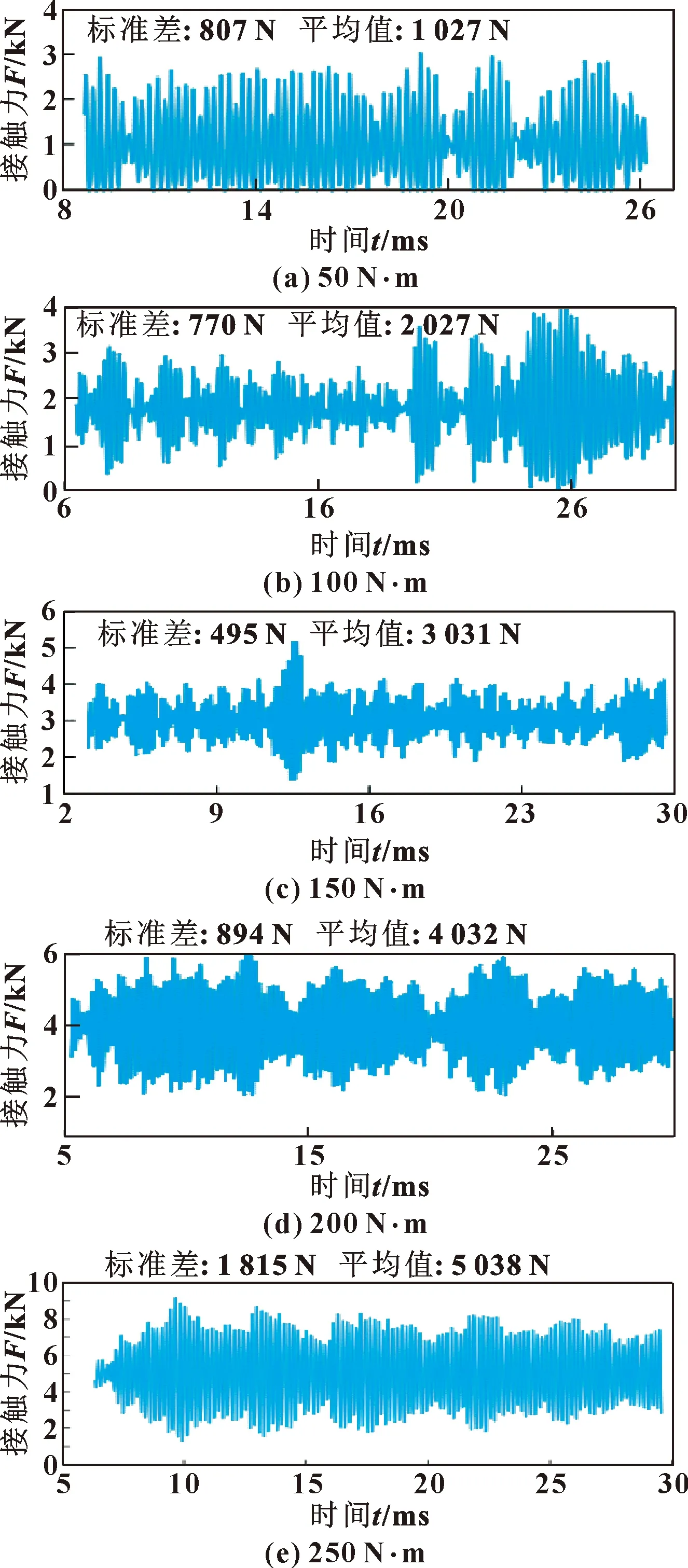
圖12 變轉矩接觸穩定性分析

首先對第一組變轉矩接觸力進行分析，從圖12中可以看出：轉矩為50 N·m時接觸力波動幅值很大，且一直有接觸為0的情況，表明在此工況下齒輪嚙合伴有脫齒現象產生，這是高速輕載工況所導致的，此工況下接觸力標準差為807 N，穩定性較差；轉矩為100 N·m時未見脫齒現象，動態接觸力變化幅值有所降低，穩定性比50 N·m時有所改善；轉矩為150 N·m時接觸趨于相對穩定狀態，標準差為495 N，穩定性最好。轉矩為200 N·m與250 N·m時接觸力變化幅值逐漸增大，接觸力穩定性逐漸變差，但并未出現脫齒現象。綜上分析可以得出接觸穩定性隨轉矩變化規律：在高速輕載時，齒輪嚙合易出現脫齒現象，且接觸穩定性較差，隨著轉矩增大齒輪接觸逐漸趨于穩定，穩定后隨轉矩不斷增大，接觸穩定性漸漸降低，但重載情況下，不會發生脫齒行為。

第二組變轉速數值計算時變接觸力如圖13所示。由圖可知：在正常負載下，所取轉速變化范圍內未見脫齒現象，轉速為500 r/min時接觸穩定性較差，在轉速為1 000 r/min時接觸穩定性最好，其余轉速下穩定性次之，但并未出現穩定性極差的情況。綜上分析可得接觸穩定性隨轉速變化規律：在正常負載情況下，合理范圍內變轉速不會造成脫齒行為，對于負載來說存在某一轉速范圍使接觸穩定性達到最佳，其余轉速接觸穩定性稍次之，且轉速對接觸穩定性影響小于轉矩。

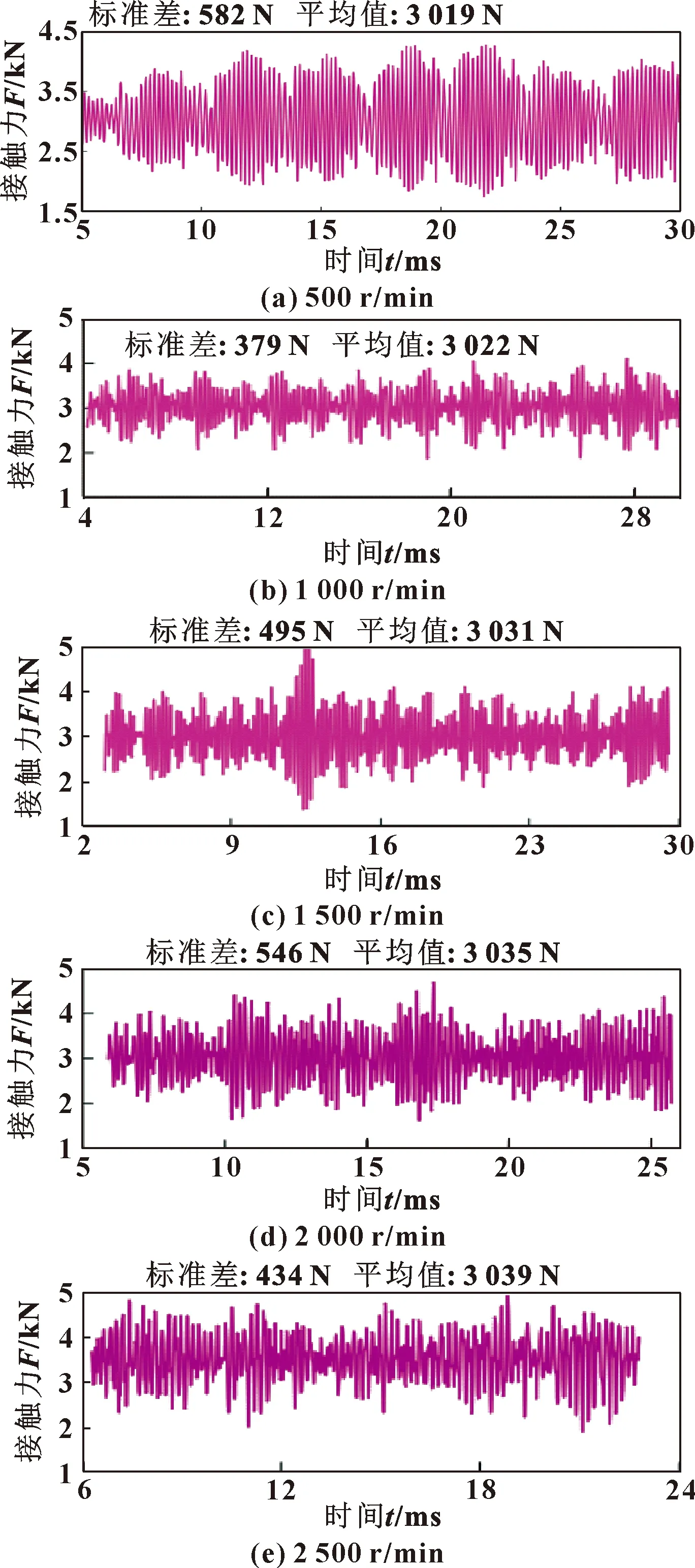
圖13 變轉速接觸穩定性分析

接觸力標準差與平均值隨工況變化規律如圖14所示，轉矩變化引起標準差的變化幅值大于轉速變化，且轉矩與接觸力平均值幾乎成正比例關系，而轉速對平均值影響不大，轉速與轉矩都存在某一最佳范圍使標準差最小。

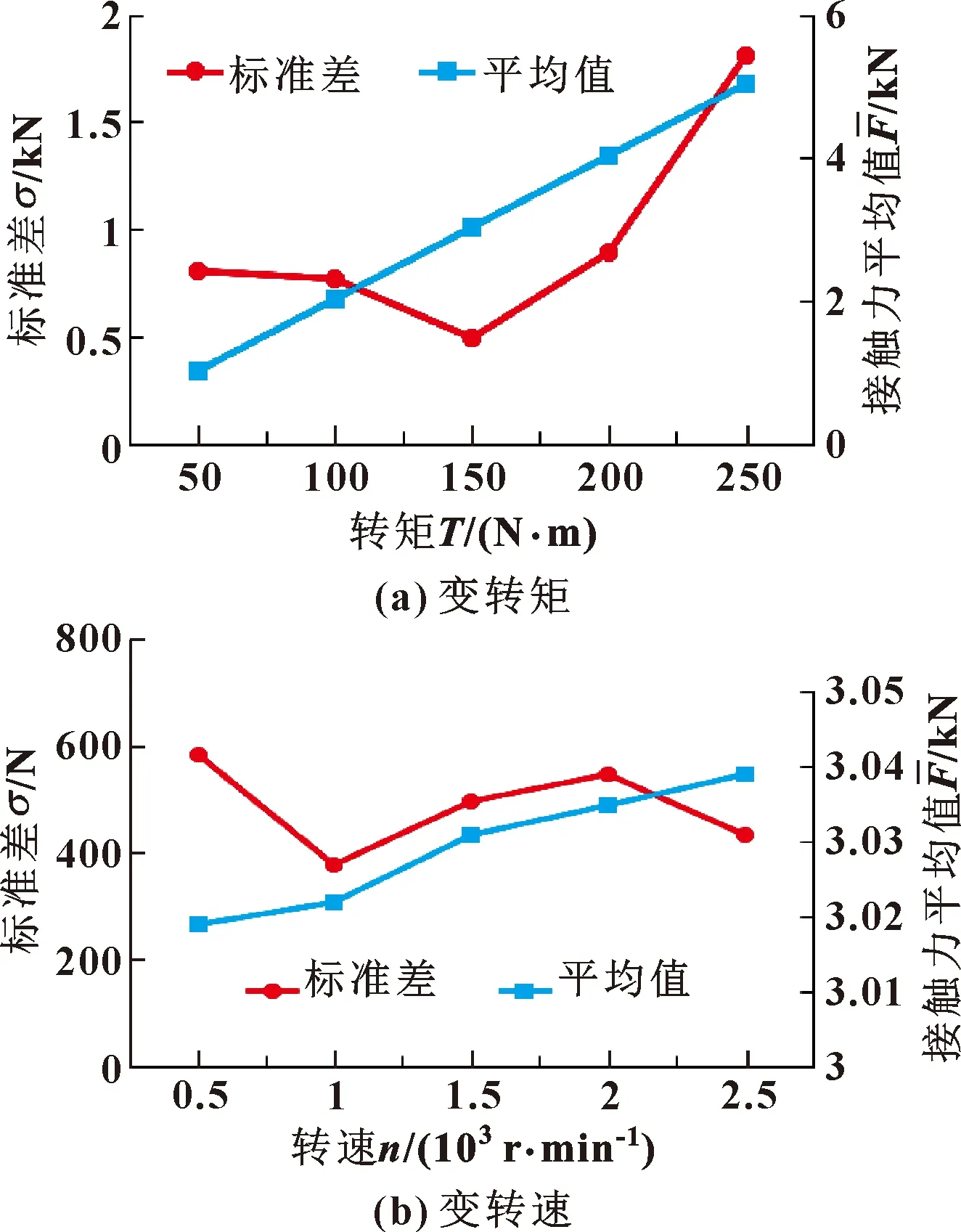
圖14 接觸力標準差與平均值變化規律

結合變工況下齒根應力與嚙合沖擊變化規律對齒輪接觸穩定性進行分析，由圖11與圖14可知轉矩變化會引起接觸力平均值、齒根應力與嚙合沖擊共同變化，說明轉矩變化導致多個狀態量共同變化，互相耦合演化，同時作用于接觸穩定性，使接觸穩定性受轉矩影響較大；而轉速變化對實際接觸力變化影響較小，僅使嚙合沖擊增大，影響接觸穩定，故接觸穩定性受轉速變化影響較小。

4 結論

文中以一對機匣齒輪為研究對象，應用反轉法確定齒輪沖擊位置，計算了不同工況下的最大沖擊力，并通過修正后的齒根應力算法計算了不同轉矩下輪齒危險截面處的齒根應力。用有限元法模擬真實工況，研究了不同工況對接觸穩定性的影響，并結合不同工況下沖擊與齒根應力對接觸穩定性進行分析，得出以下結論：

(1)主動輪齒根應力小于從動輪，且主從動輪的齒根應力均隨轉矩增大而增大，齒根應力隨轉速變化較小。嚙合沖擊力隨轉速與轉矩的增大而增大，且隨著轉矩增大，沖擊力的增大趨勢減緩，而沖擊力與轉速幾乎成正比關系增長。

(2)在高速輕載時，齒輪嚙合易出現脫齒現象，且接觸穩定性較差，隨著轉矩增大嚙合逐漸趨于穩定，穩定后隨轉矩不斷增大，接觸穩定性漸漸降低，但重載情況下，不會發生脫齒行為。

(3)在正常負載情況下，合理范圍內變轉速不會造成脫齒行為，對于負載來說存在某一轉速范圍使接觸穩定性達到最佳，其余轉速接觸穩定性稍次之，且轉速對接觸穩定性影響小于轉矩。

(4)轉矩變化會引起接觸力、齒根應力與嚙合沖擊共同變化，接觸穩定性受轉矩影響較大，而轉速變化僅導致嚙合沖擊力變化，對實際接觸力變化影響較小。在實際應用中，結合以上分析規律，針對負載選取相應的轉速能極大提高齒輪運轉接觸穩定性。