對(duì)一道中考幾何壓軸題的探究與反思

董濤

［摘? 要］ 2021年福建省中考數(shù)學(xué)試卷第25題是一道以正方形為背景，證明線段數(shù)量關(guān)系為定值的幾何壓軸題，該題的圖形結(jié)構(gòu)經(jīng)典，能一題多解，可考查學(xué)生的思維廣度、深度、創(chuàng)造性及解題能力，文章對(duì)此題圖形結(jié)構(gòu)進(jìn)行分析，并探究解法、拓展延伸、解后反思.

［關(guān)鍵詞］ 數(shù)量關(guān)系；構(gòu)造；含參運(yùn)算；一題多解

試題呈現(xiàn)

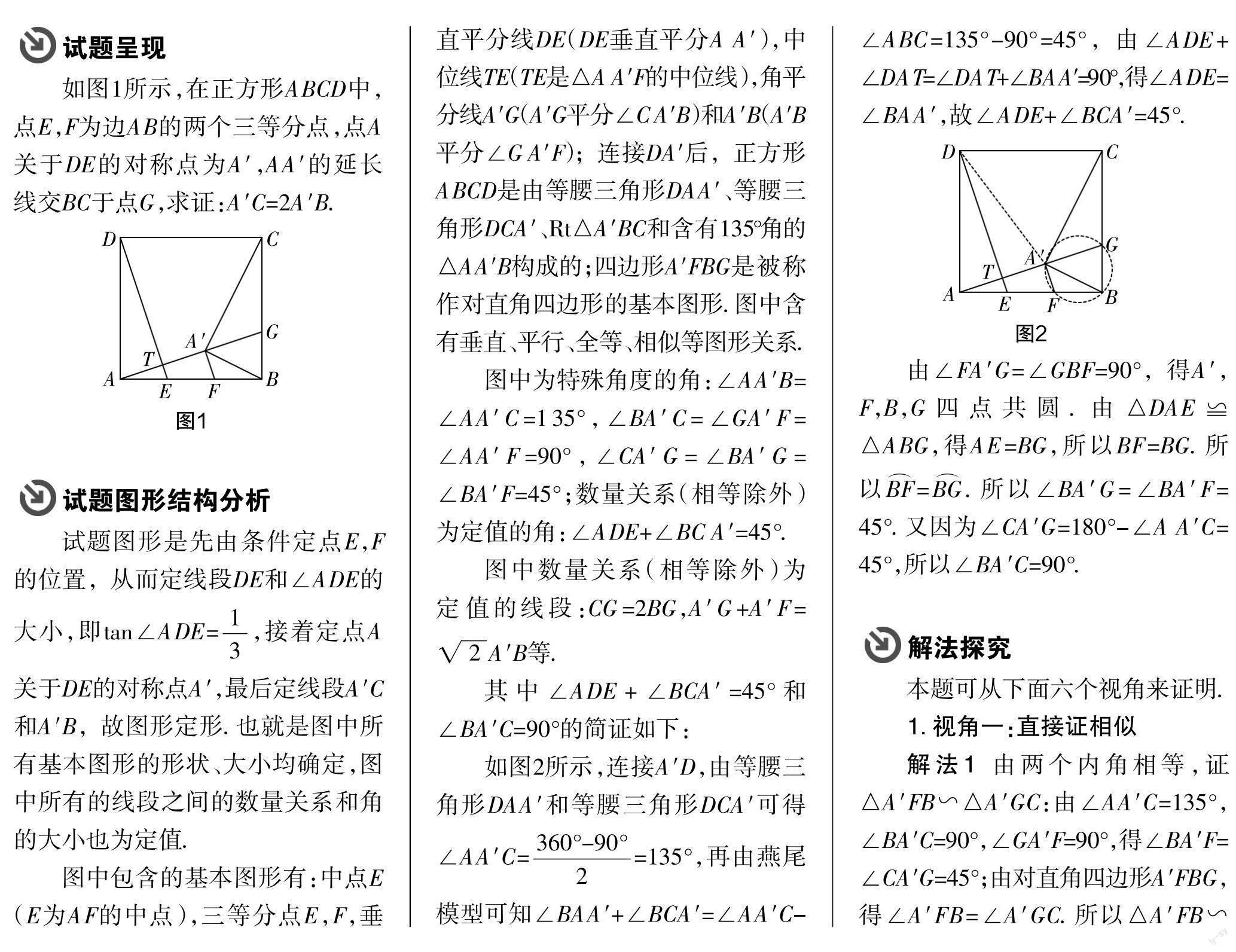
如圖1所示，在正方形ABCD中，點(diǎn)E，F(xiàn)為邊AB的兩個(gè)三等分點(diǎn)，點(diǎn)A關(guān)于DE的對(duì)稱點(diǎn)為A′，AA′的延長線交BC于點(diǎn)G，求證：A′C=2A′B.

解后反思

1. 執(zhí)果索因，為何定形

定形的根本原因一定是數(shù)，三角形定形往往是因?yàn)榫邆渑卸▋蓚€(gè)三角形相似的條件，如定兩個(gè)角的大小、定三邊比值不變、定兩邊比值不變及定一角大小等.追尋定形原因，有助于探尋求解思路，恰當(dāng)?shù)剡M(jìn)行邊角轉(zhuǎn)化.

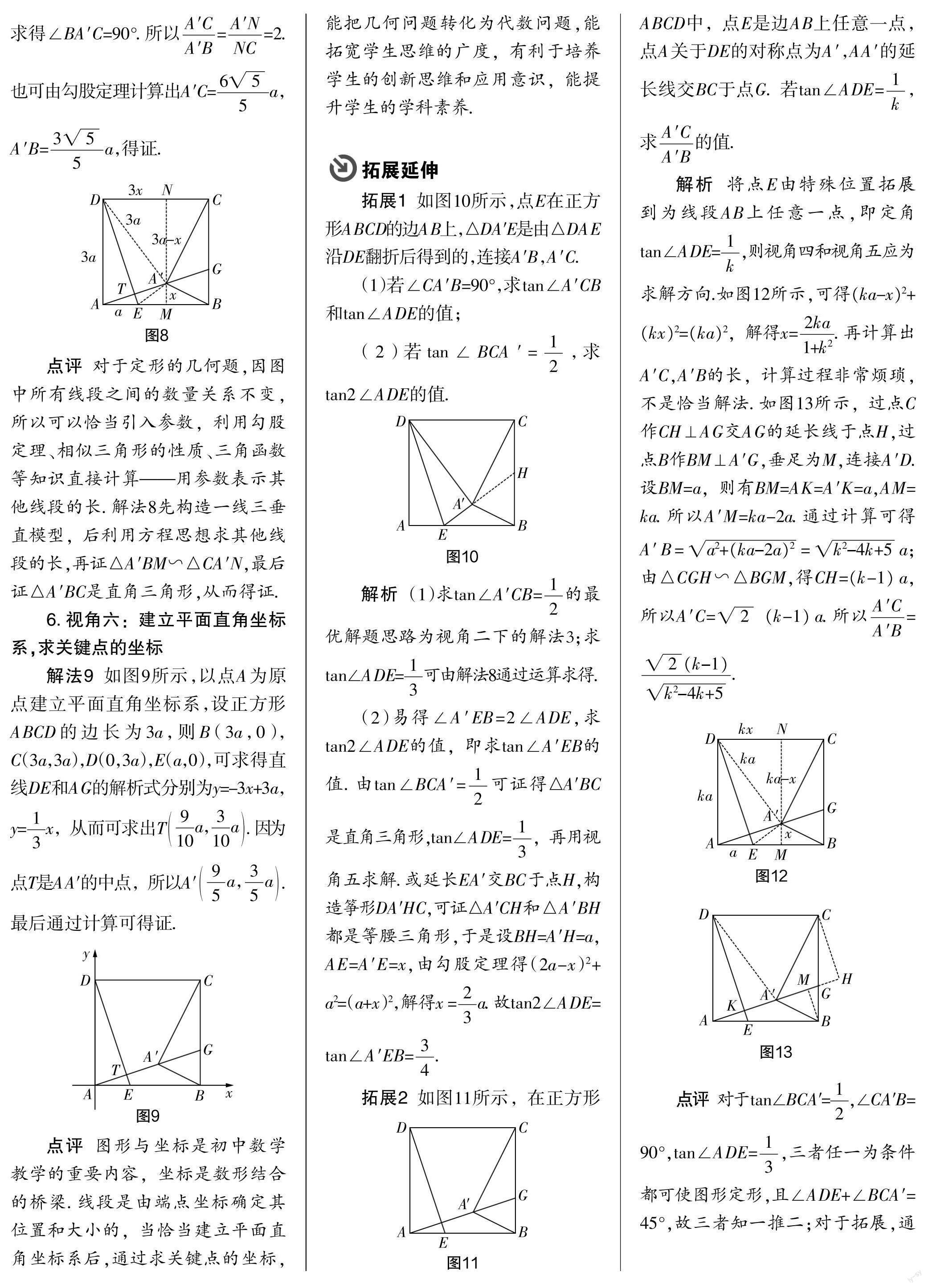
2. 明確構(gòu)圖過程，分析圖形結(jié)構(gòu)

一個(gè)復(fù)雜圖形的生成就是在題目條件不斷累積下一個(gè)又一個(gè)基本圖形的有序組合，當(dāng)出現(xiàn)等邊三角形、等腰直角三角形時(shí)，圖中就會(huì)有特殊角度的角、數(shù)量關(guān)系不變的角和線段、中點(diǎn)、角平分線、垂直平分線、中位線，全等或相似等關(guān)系的圖形，這些都為后面數(shù)量關(guān)系的轉(zhuǎn)化和線段長度的計(jì)算提供了條件.

3. 探尋橋梁，確定求解方法

對(duì)于定形的幾何綜合題，題目條件通常沒有具體線段的長度，無論直接聯(lián)系，還是間接聯(lián)系，都需引入?yún)?shù)進(jìn)行運(yùn)算. 求解時(shí)要能恰當(dāng)?shù)剡x擇勾股定理、相似三角形的性質(zhì)或三角函數(shù)進(jìn)行直接計(jì)算或列方程.

4. 構(gòu)造基本圖形或關(guān)系圖形，提升運(yùn)算能力

幾何背景下的運(yùn)算同空間觀念、邏輯推理能力分不開，這里的運(yùn)算能力指的是通過識(shí)別、構(gòu)造基本形和關(guān)系圖形進(jìn)行簡化運(yùn)算. 構(gòu)造的關(guān)鍵是發(fā)現(xiàn)圖中不變的幾何量.

5. 滲透模型思想和構(gòu)造思想

將“模型思想和構(gòu)造思想”滲透進(jìn)初中幾何教學(xué)之中，既可以增強(qiáng)學(xué)生的空間觀念和創(chuàng)新意識(shí)、應(yīng)用意識(shí)，又能培養(yǎng)學(xué)生的思維能力，提高學(xué)生的數(shù)學(xué)學(xué)科素養(yǎng).