利用數(shù)學(xué)模型分析基坑降水影響半徑的風(fēng)險(xiǎn)
盧丙玉
(中鐵二十二局集團(tuán)市政工程有限公司,廣東 廣州 510000)
0 引言
隨著社會(huì)進(jìn)一步發(fā)展,人們對(duì)基礎(chǔ)建設(shè)的要求越來(lái)越高,尤其是城市建設(shè),為了提高土地利用率,正朝著更高、更快、更深的方向發(fā)展,并呈現(xiàn)出越來(lái)越多的超高層建筑、高速交通、大型深基坑基礎(chǔ)設(shè)施。由于深基坑開挖會(huì)對(duì)土體造成擾動(dòng),使得土體發(fā)生位移變形,繼而對(duì)基坑支護(hù)結(jié)構(gòu)及周邊建筑物結(jié)構(gòu)安全構(gòu)成很大危害,因此控制基坑開挖過(guò)程變形成為重中之重[1-2]。基坑穩(wěn)定是一個(gè)復(fù)雜的工程問題,在土體開挖過(guò)程中,既需要考慮土體本身的強(qiáng)度與穩(wěn)定性因素,還須考慮水的滲流作用導(dǎo)致的變形問題,以及基坑變形對(duì)周邊建筑物的影響,因此傳統(tǒng)的土力學(xué)理論分析已無(wú)法滿足要求。本文通過(guò)構(gòu)建數(shù)學(xué)模型,利用數(shù)學(xué)模型進(jìn)行了基坑降水影響半徑的風(fēng)險(xiǎn)研究。
1 工程概況
某基坑工程位于廣州市花都區(qū),工程施工點(diǎn)東南側(cè)緊鄰新街河,其余方向均有住宅區(qū),且多為高層建筑,該處地下水位較高,在2m~7m之間,多年平均變幅在2m~4m,經(jīng)現(xiàn)場(chǎng)土體鉆探取芯發(fā)現(xiàn),土體層依次為雜填土層、黏性土層、中粗砂層、強(qiáng)風(fēng)化巖層,水文地質(zhì)復(fù)雜。基坑開挖深度為12m,基坑安全等級(jí)為一級(jí)。工作坑底板尺寸為長(zhǎng)32m,寬16.5m,沿基坑外緣2m處布置管井降水點(diǎn),每個(gè)降水點(diǎn)間隔距離為6m,共布置17處,基坑內(nèi)布置5口疏干井。
2 降水?dāng)?shù)學(xué)模型
2.1 滲流方程
假設(shè)在單位降水時(shí)間里,一單位面積內(nèi)微分土體單元降水入滲強(qiáng)度W,流經(jīng)該土體微分單元的流量為q,通過(guò)該土體微分單元后流量為q+dg,滲流場(chǎng)示意如圖1所示。
按達(dá)西公式,假設(shè)在距降水井中心r處,選取一圓環(huán)土體微分單元作為研究對(duì)象,如圖2所示,該圓環(huán)土體微分單元厚度為dr,經(jīng)降水時(shí)間t后,降水深度為H,流入圓環(huán)土體微分單元為Qr,則通過(guò)該圓環(huán)土體微分單元后的流量為如圖2所示。
則流量可以表示為:
K為滲透系數(shù),經(jīng)降水時(shí)間t后獲得的總增量為:
經(jīng)降水時(shí)間t后,在環(huán)形面積2πrdr中滲入的水量為:
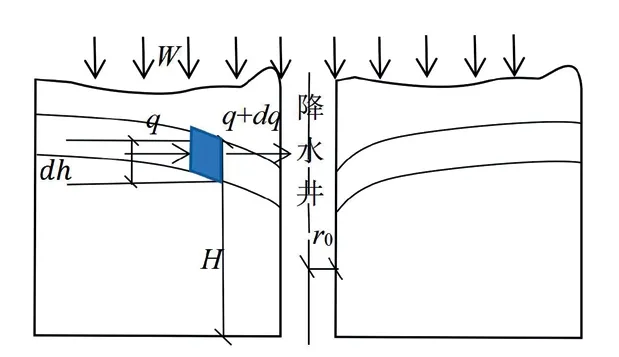
圖1 滲流場(chǎng)示意圖
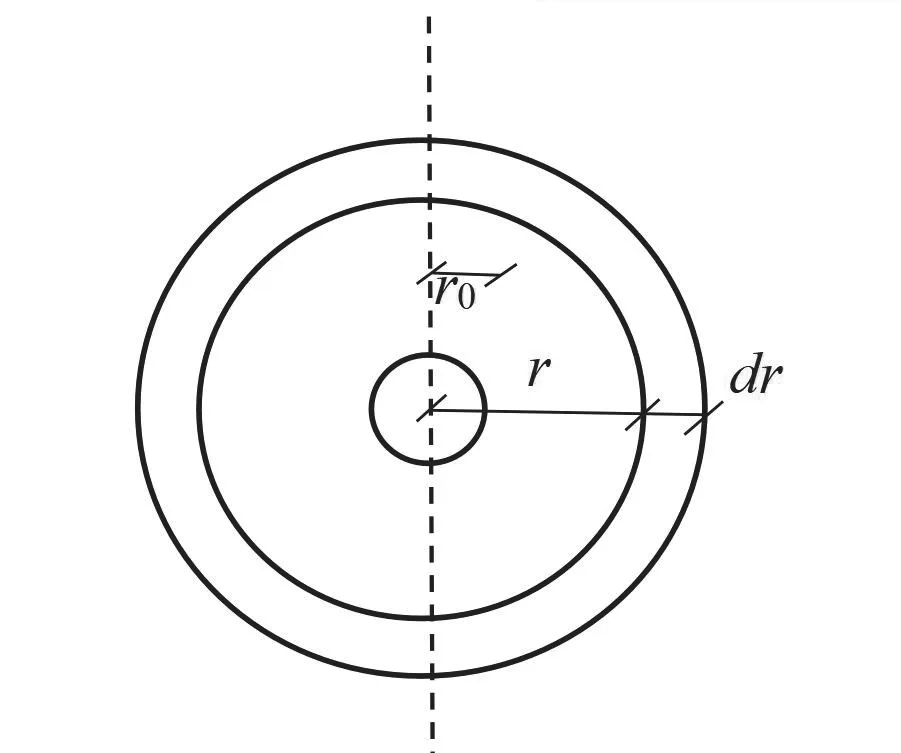
圖2 圓環(huán)土體微分單元
經(jīng)降水時(shí)間t后,微分土體單元中降水量:
式中:μ為給水度。理論上,在微分土體單元中,滲入的水量和降水量應(yīng)與獲得的增量平衡,則有:
整理得到降水高度與時(shí)間關(guān)系為:
已知降水時(shí)間t內(nèi),平均含水層厚度為HP,代入公式7中,則有:
當(dāng)降水入滲強(qiáng)度W=0時(shí),則有:
2.2 降水?dāng)?shù)學(xué)模型
當(dāng)降水時(shí)間t=0時(shí),含水層水位高度H0為初始水位高度,假設(shè)在距抽水井中心r=R0處水位無(wú)變化,則降水時(shí)水位狀態(tài)數(shù)學(xué)模型為:
2.3 數(shù)學(xué)模型求解
根據(jù)本工程項(xiàng)目實(shí)際水文地質(zhì)條件對(duì)降水模型參數(shù)進(jìn)行設(shè)置,含水層初始厚度H0=18.0m,地下水位埋深3m,滲透系數(shù)K=0.4m/d,給水度μ=0.1,抽水井半徑r0=0.25m,假設(shè)抽水井等效半徑R0=70m,期間不計(jì)補(bǔ)給,抽水降深需達(dá)到15m。利用MATLAB軟件中pdepe函數(shù),計(jì)算15d期的降水情況,函數(shù)運(yùn)算過(guò)程如下:
3 數(shù)學(xué)模型計(jì)算結(jié)果分析和監(jiān)測(cè)對(duì)比
3.1 降水影響半徑
通過(guò)對(duì)數(shù)學(xué)模型計(jì)算結(jié)果的整理,以降水點(diǎn)與降水井的距離作為影響半徑的橫坐標(biāo),以地下水位高度作為縱坐標(biāo),分析降水對(duì)周邊建筑物的影響范圍。
隨著降水時(shí)間的延長(zhǎng),地下水位下降深度越大,并且在60m影響半徑范圍內(nèi)時(shí),當(dāng)降水點(diǎn)與降水井的的距離越小,水位下降深度越明顯,降水效果越好;當(dāng)影響半徑>60m時(shí),降水效果不明顯,降水后地下水位趨近于原地下水位埋深。在60m影響半徑范圍內(nèi),與降水井距離越小,水頭越大,降水對(duì)地面沉降變形影響越大,應(yīng)做為地面沉降重點(diǎn)監(jiān)控區(qū)域,選取現(xiàn)場(chǎng)監(jiān)測(cè)數(shù)據(jù)與數(shù)學(xué)模型計(jì)算結(jié)果做對(duì)比,來(lái)佐證數(shù)學(xué)模型計(jì)算結(jié)果的可信度。
從圖3可知,理論計(jì)算值接近實(shí)際監(jiān)測(cè)值,說(shuō)明該數(shù)學(xué)模型能較好地模擬基坑降水,具有很大的參考價(jià)值。
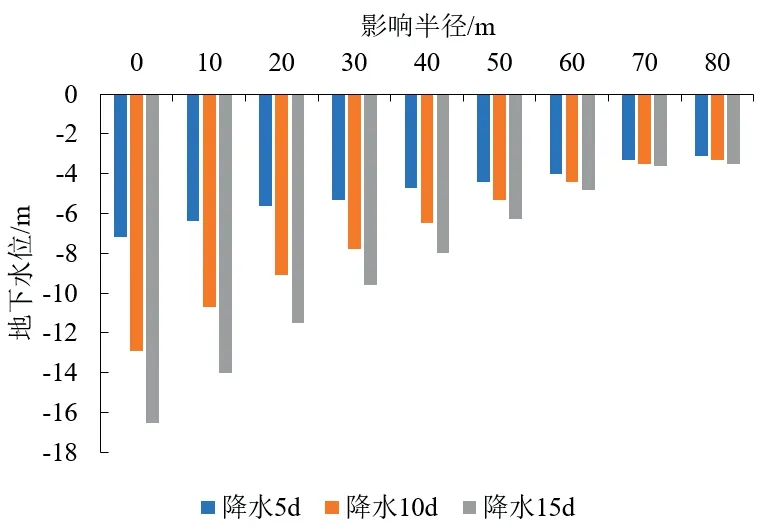
圖3 降水影響半徑
3.2 地表沉降變形
地表沉降變形監(jiān)測(cè)貫穿整個(gè)基坑降水作業(yè)過(guò)程,既是基坑降水深度的指南,也是施工安全的保證,通過(guò)整理監(jiān)測(cè)數(shù)據(jù),以實(shí)際監(jiān)測(cè)的地表沉降變形大小來(lái)佐證降水?dāng)?shù)學(xué)模型的準(zhǔn)確性,地表沉降變形大小。
隨著開挖深度的增加,地表沉降變形量也不斷增大,并且表現(xiàn)為變形量梯度先大后小;其次,距降水井10m處變形量是最大的,應(yīng)重點(diǎn)監(jiān)控,提前做好防護(hù);當(dāng)距降水井>45m時(shí),地表沉降變形量不再增長(zhǎng),說(shuō)明數(shù)學(xué)模型計(jì)算的影響半徑是可信的。
4 結(jié)束語(yǔ)
根據(jù)滲流理論,建立降水?dāng)?shù)學(xué)模型,再根據(jù)設(shè)定的條件由數(shù)學(xué)模型計(jì)算出降水影響半徑,以此確定降水對(duì)周邊建筑物的影響半徑是60m。
選取現(xiàn)場(chǎng)監(jiān)測(cè)數(shù)據(jù)和數(shù)學(xué)模型計(jì)算的水位降深結(jié)果做對(duì)比,發(fā)現(xiàn)數(shù)學(xué)模型計(jì)算的結(jié)果與實(shí)際監(jiān)測(cè)數(shù)據(jù)接近,具有很大的參考價(jià)值。
通過(guò)現(xiàn)場(chǎng)地表沉降變形量監(jiān)測(cè),發(fā)現(xiàn)距降水井10m處變形量最大,應(yīng)重點(diǎn)監(jiān)控并做好防護(hù);當(dāng)距降水井>45m時(shí),地表沉降變形量不再增長(zhǎng)。

