新文科背景下政產學研協同育人演化博弈研究

胡 奇,徐茗臻

(1.江西理工大學 經濟管理學院;2.贛南科技學院 資源與建筑工程學院,江西 贛州 341000)

0 引言

近年來,“新文科”人才的培育在我國高等教育中的地位迅速提升,是我國高等教育頂層設計中關于文科專業(yè)建設的重要任務[1-2]。對于新文科人才的培育需要做到:①對企業(yè)進行升級改造;②增設更能符合社會發(fā)展需求的新專業(yè);③構建社會人才培育體系以及提供充足的培育經費。在培育過程中,多主體分工合作是新文科人才培育的主要手段[3],以學校、企業(yè)、政府為主體的政產學研分別在技術、資金、政策方面給予支持和幫助[4]。但由于政府缺乏剛性的監(jiān)管機制、企業(yè)缺乏合作的動力以及新文科人才培育機制還不完善,協同育人項目難以形成長期穩(wěn)定的合作。因此,如何調節(jié)合作主體之間的關系對于新文科人才培育以及維持聯盟關系尤為重要。通過博弈論創(chuàng)立各主體利益分配模型[5-6],對主體進行合作博弈問題分析,從而了解各主體行為對合作關系的影響。

演化博弈模型對政產學研穩(wěn)定性的研究表明演化過程受到初始狀態(tài)影響,與利益分配、獎懲金額也密切相關[7],而在市場機制下采取適當的獎懲機制可以維持合作穩(wěn)定[8-9]。因此,在演化博弈研究中,需要給定初始合作狀態(tài)、建立獎懲機制,并考慮市場機制和政府調控對合作各方博弈的影響。

本文基于演化博弈論建立了市場機制和政府調控下協同培育新文科人才的模型,分析了在不同情況下企業(yè)與學研機構做出的決策以及聯盟穩(wěn)定性的影響因素。研究表明,初始條件的設置會對聯盟的穩(wěn)定性產生影響,且穩(wěn)定的聯盟會提高新文科人才培養(yǎng)帶來的收益;同時,政府采取協同育人的管控機制可以增強聯盟的穩(wěn)定性。

1 市場機制下政產學研協同育人博弈模型

學研機構、企業(yè)、政府均是利益相關者:學研機構主要負責協同育人創(chuàng)新,企業(yè)主要負責投入和技術轉化,政府負責激勵行為主體參與合作。所以在協同育人過程中,需考慮每個主體參與協同育人的投入與收益,以及其行為決策對合作的影響。各合作者間的演化博弈分析及各主體關系如圖1所示。

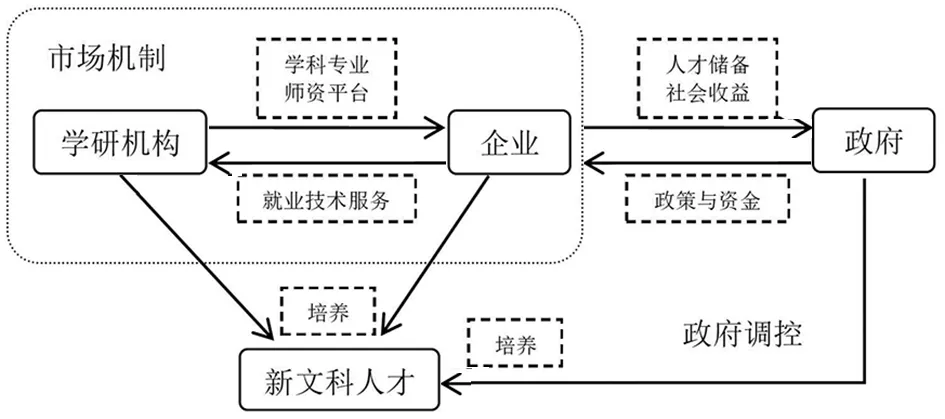
圖1 新文科協同育人各主體間關系

1.1 模型假設

對本文涉及的博弈理論模型,作出以下假設:①假設參與各方掌握的信息具有不對稱性,且追求利益的最大化;②博弈的雙方都處在博弈初始階段,各主體會通過多次博弈來獲取最優(yōu)策略。

1.1.1 企業(yè)行為假設

企業(yè)在博弈過程中的策略選擇為“參與合作”與“不參與合作”,對應的初始概率分別為x1和1-x1,x1范圍為0至1。“參與合作”是指企業(yè)在遵循政府制定的獎懲機制下,選擇與學研機構共同培育新文科人才的策略;“不參與合作”是指企業(yè)不選擇與學研機構共同培育新文科人才的策略。

1.1.2 學研機構行為假設

學研機構在博弈過程中的策略選擇為“參與合作”與“不參與合作”,對應的初始概率分別為y1和1-y1,y1的范圍是0至1。“參與合作”是指學研機構在遵循政府制定的獎懲機制下,選擇與企業(yè)共同培育新文科人才的策略;“不參與合作”是指學研機構不選擇與企業(yè)共同培育新文科人才的策略。

1.2 其他變量設置

1.2.1 企業(yè)

假設L1為企業(yè)參與協同育人項目前的初始收益;R1為企業(yè)選擇“參與合作”策略后的收益;C1為企業(yè)選擇“參與合作”策略后的成本;G1為企業(yè)選擇“參與合作”策略時政府給予的補貼;當政府提供政產學研協同育人優(yōu)惠政策時,企業(yè)可降成本,β為政策支持力度,故βC1則為企業(yè)降低成本。

1.2.2 學研機構

假設L2為學研機構參與協同育人之前的初始收益;R2為學研機構選擇“參與合作”策略后的收益;α為企業(yè)與學研方合作收益的分攤比例系數,則企業(yè)的收益為α(R1+R2),學研機構對應的收益為(1-α)(R1+R2);C2為企業(yè)選擇“參與合作”策略后的成本;G2為企業(yè)選擇“參與合作”策略時政府給予的補貼;故學研機構降低成本為βC2。

1.2.3 懲罰

若企業(yè)與學研機構中途退出,W為退出方支付的罰金,π為退出方在協同育人合作過程中獲得的溢出收益。

以上所有參數均大于0,且α和β均為0至1范圍內的實數。學研機構和企業(yè)選擇合作或不合作策略時,雙方所取得的收益矩陣如表1。

表1 市場機制下政產學研協同育人策略矩陣

1.3 企業(yè)與學研機構的復制動態(tài)方程

1.3.1 企業(yè)

企業(yè)選擇“參與合作”或“不參與合作”的期望收益,如式(1)和(2)。

U1=y1[L1+α(R1+R2)+G1+βC1-C1]+(1-y1)(L1+W+G1+βC1-C1)=y1[α(R1+R2)-W]+L1+W+G1+βC1-C1

(1)

(2)

由式(1)和(2)可以得到企業(yè)的平均期望收益,如式(3)。

(3)

根據平均期望收益,可以得到企業(yè)選擇“參與合作”策略概率的復制動態(tài)方程,如式(4)。

F1(x)=x1(1-x1)

{[α(R1+R2)-π]y1+W+G1+βC1-C1}

(4)

1.3.2 學研機構

學研機構選擇“參與合作”或“不參與合作”的期望收益,如式(5)和(6)。

V1=x1[L2+(1-α)(R1+R2)+G2+βC2-C2]+(1-x1)(L2+W+G2+βC2-C2)=x1[(1-α)

(R1+R2)-W]+L2+W+G2+βC2-C2

(5)

(6)

根據式(5)和(6),得到學研機構平均期望收益,如式(7)。

(7)

由上式可以得到學研機構選擇“參與合作”策略概率的復制動態(tài)方程,如式(8)。

F1(y)=y1(1-y1)[(1-α)(R1+R2)-π]x1+W+G2+βC2-C2

(8)

1.4 市場機制下政產學研協同育人策略均衡點穩(wěn)定性分析

(9)

將企業(yè)與學研機構的復制動態(tài)方程如式(9),得到系統(tǒng) Jacobi 矩陣如下:

(0≤a≤1,0≤b≤1),E5(a,b)為鞍點,屬于不穩(wěn)定狀態(tài),故演化穩(wěn)定狀態(tài)為E1(0,0),E2(0,1),E3(1,0),E4(1,1),分析如下:

結論一:當W+G1+βC1-C1與W+G2+βC2-C2小于0時,企業(yè)和學研機構在市場監(jiān)管機制下相互博弈、相互制約,最后均不參與協同育人項目,此時(0,0)為博弈的演化穩(wěn)定點,即企業(yè)需要做出自身利益最大化的決策。然而企業(yè)與學研機構在政府支持下參與協同育人項目的育人成本大于政府的補貼與對方退出所得到的罰金,即企業(yè)與學研機構的總收益均小于成本。在此條件下,協同育人項目承擔的風險較大,因此企業(yè)與學研機構選擇“不參加合作”策略。

結論二:當α(R1+R2)-π+W+G1+βC1-C1小于0而W+G2+βC2-C2大于0時,演化博弈穩(wěn)定點為(0,1),此時學研機構會參與協同育人項目,但是企業(yè)會退出協同育人項目。原因是:α(R1+R2)-π+W+G1+βC1-C1可以轉化為α(R1+R2)+G1+βC1-C1小于π-W,即企業(yè)參加協同育人的經濟收益小于中途退出的收益。故在多次博弈后,企業(yè)會選擇退出協同育人項目;對于學研機構,得到的政府補貼與企業(yè)的罰金大于合作初成本,不會造成經濟損失。最終,協同育人項目由學研機構單獨進行。

結論三:當W+G1+βC1-C1大于0而(1-α)(R1+R2)-π+W+G2+βC2-C2小于0時,演化博弈點為(1,0)。此時,企業(yè)會參與協同育人項目,但學研機構會選擇退出與協同育人項目。具體來說:(1-α)(R1+R2)-π+W+G2+βC2-C2小于0可以轉化為(1-α)(R1+R2)+G2+βC2-C2小于π-W,即企業(yè)得到學研機構退出的罰金與政府補貼之和大于合作的成本;學研機構退出合作的收益要大于參與協同育人項目時的收益。故在經過多次博弈后,與結論二相似,協同育人項目最終僅有企業(yè)參與。

結論四:α(R1+R2)-π+W+G1+βC1-C1與(1-α)(R1+R2)-π+W+G2+βC2-C2均大于0時,演化博弈穩(wěn)定點為(1,1),此時企業(yè)與學研機構均會堅持新文科協同育人項目。這一現象解釋為:α(R1+R2)-π+W+G1+βC1-C1大于0可轉變?yōu)棣?R1+R2)+G1+βC1-C1大于π-W,此時企業(yè)參與協同育人項目的收益大于退出合作時的收益,所以企業(yè)會選擇繼續(xù)協同育人項目。同理,(1-α)(R1+R2)-π+W+G2+βC2-C2大于0,可轉變?yōu)?1-α)(R1+R2)+G2+βC2-C2大于π-W,則學研機構參與協同育人項目的收益大于不參與協同育人項目的收益,同樣會選擇繼續(xù)參與協同育人項目。因此,雙方均會選擇“參與合作”策略。

2 政府調控下政產學研協同育人博弈模型

2.1 模型假設

2.1.1 企業(yè)與學研機構行為假設

企業(yè)在博弈過程中的策略選擇為“參與合作”與“不參與合作”,對應的初始概率分別為x2和1-x2,x2范圍為0至1。

2.1.2 政府行為假設

政府在博弈過程中的策略選擇為“參與調控”與“不參與調控”,對應的初始概率分別為y2和1-y2,y2的范圍是0至1。

2.2 其他變量設置

2.2.1 企業(yè)與學研機構

假設:L為企業(yè)和學研機構在參與協同育人前的收益;R為企業(yè)和學研機構選擇“參與合作”策略后的收益;R'僅一方參與項目后獲得的收益;C為企業(yè)和學研機構選擇“參與合作”策略后的成本;G為企業(yè)和學研機構選擇“參與合作”策略時政府給予的補貼。

2.2.2 政府

假設S為政府調控時企業(yè)和學研機構參與合作產生的社會收益,δS為政府不調控時企業(yè)和學研機構參與合作時政府獲得的社會收益;S'為政府參與調控時僅一方參與合作產生的社會收益,εS'為政府不參與調控且僅一方參與合作產生的社會收益;F為政府選擇“參與調控”策略時的成本。

以上所有參數均大于0,且δ和ε均為0至1范圍內的實數,根據以上假設得出企業(yè)和學研機構與政府的收益矩陣如表2。

表2 政府調控下政產學研協同育人策略矩陣

2.3 企業(yè)和學研機構與政府的復制動態(tài)方程

基于表2博弈支付矩陣,遵循上述計算博弈主體的期望收益、平均期望收益與復制動態(tài)方程的步驟,得到政府參與調控下博弈主體相應的復制動態(tài)方程組,如式(10)、(11):

F2(x2)=x2(1-x2)(Gy2+R-R'-C)

(10)

F2(y2)=y2(1-y2){[(1-δ)S-(1-ε)S'-G-F]x2+(1-ε)S'}

(11)

2.4 政府調控下政產學研協同育人均衡點穩(wěn)定性分析

與市場機制分析步驟相同,政府調控下的 Jacobi 矩陣為,見式(12):

(12)

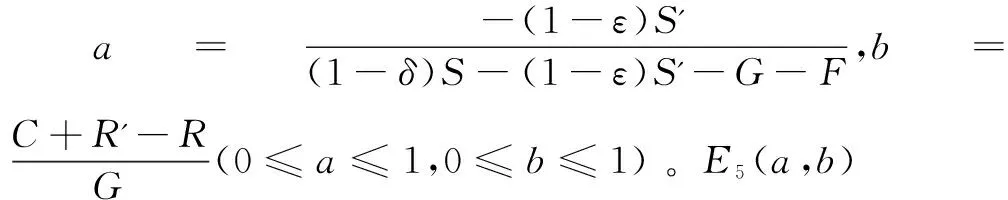
結論五:當R-R'-C小于0且(1-ε)S'小于0時,此時(0,0)為系統(tǒng)演化穩(wěn)定點,企業(yè)和學研機構、政府經過反復博弈,最終形成不合作、不調控的局面。原因是企業(yè)和學研機構合作產生的收益小于單方參與的收益,而政府的調控收益小于不調控產生的收益。最終導致企業(yè)和學研機構均放棄參與合作,且政府也會采取“不調控”策略。

結論六:當G+R-R'-C小于0且(1-ε)S'大于0時,此時(0,1)為系統(tǒng)演化穩(wěn)定點,企業(yè)和學研機構合作的收益與政府的補貼之和小于僅一方參與協同育人的收益,最終采取“不合作”策略;而政府參與調控新文科人才的培育收益大于不參與調控的收益,會采取繼續(xù)“調控”策略。

結論七:當R-R'-C大于0且(1-δ)S-G-F小于0,此時博弈的穩(wěn)定點為(1,0),對于企業(yè)和學研機構而言,雙方參與合作的收益大于僅一方參與協同育人帶來的經濟收益,故會選擇“合作”策略;(1-δ)S-G-F小于0可轉變?yōu)镾-G-F小于δS,說明政府調控的收益減去補貼與成本之和小于不調控新文科協同育人帶來的收益,故經過多次博弈后,最終選擇“不調控”策略。

結論八:當G+R-R'-C與(1-δ)S-G-F大于0時,穩(wěn)定點為(1,1),表明企業(yè)和學研機構會參與協同育人,且政府會參與調控,監(jiān)督聯盟。G+R-R'-C大于0轉變?yōu)镚+R-C大于R',說明企業(yè)和學研機構參與協同育人帶來的收益與政府補貼之和大于僅一方參與的收益,此時選擇“合作”策略;(1-δ)S-G-F大于0轉化為S-G-F大于δS,說明政府獲得的收益大于調控投入的成本和補貼的成本之和,最終會選擇“調控”策略。

3 結論與啟示

3.1 研究結論

本文基于演化博弈理論,探究新文科背景下,政府、學研機構和企業(yè)如何在市場機制與政策調控下進一步開展政產學研協同育人項目,并得出以下結論:

(1)市場機制下企業(yè)與學研機構協同育人的穩(wěn)定程度與設置的罰金、政府的補貼、收益分攤系數以及政府支持力度有關,政府在資金、政策上給予的支持力度越大,越容易促成企業(yè)與學研機構的合作。

(2)政府采取的調控措施影響管理過程中的穩(wěn)定性,政府應在新文科人才培養(yǎng)過程中適當增加監(jiān)督成本等以提高合作的穩(wěn)定性,從而獲得穩(wěn)固收益。

(3)本文運用博弈論,通過分析新文科人才培養(yǎng)主體決策的相互影響,豐富了政產學研協同培育新文科人才的理論體系,為我國新文科人才的培養(yǎng)提供了一定思路與方向,具有一定的現實意義。

由于我國新文科建設的時間較短,實踐較少,本文無法較為準確地設置演化博弈過程中的具體參數。在今后的研究中需不斷細化演化過程中的具體參數,通過仿真分析研究不同初始條件下政產學研合作穩(wěn)定性的影響因素。

3.2 管理啟示

(1)政府調控是新文科人才培養(yǎng)項目增收、提質的關鍵。政府應積極加強對政產學研協同育人項目的政策支持,通過協調、調控各主體間的收支平衡,建立適當的獎懲機制來推動新文科人才培養(yǎng)事業(yè)的發(fā)展。

(2)各主體應適當增加對學研機構的幫助與支持。學研機構不同于企業(yè),其主要收入來源是新文科人才培養(yǎng)項目收益。當學研機構出現項目虧損時,相對于企業(yè)來說,由于缺少足夠的財政支撐,其往往更容易中止項目。因此政府與企業(yè)應該在資源上為其提供適當的幫助,推動和增強學研機構參與合作的意愿。

(3)應加強對新文科人才培養(yǎng)項目的政策宣傳和設備支持。政府應積極宣傳新文科人才培養(yǎng)的現實意義,努力調動新文科人才培養(yǎng)主體的積極性,以實現政產學研深度融合。