HPM 視角下解密楊輝三角與二項式系數的關系

廣東省汕頭市聿懷中學(515000) 曾祥榮

1 引言

數學史與數學教育(HPM)流傳較廣、影響較大,深受一線教師的喜愛與關注. 目前,融入數學史的教育實踐和教學設計層出不窮,但關于中國數學史融入課堂教學的研究并不多見. 楊輝三角是我國數學家的杰出成果之一,也是流傳較廣的數學史料,其教育價值不可忽視. 通過解密楊輝三角與二項式系數的關系,能揭示二項式系數的變化規律與眾多性質. 因此,楊輝三角是不可多得的集文化魅力、數學趣味、德育功效于一體的理想教學材料.

該內容是在選修2-3“二項式定理”一節的基礎上,參考教科書中“探究與發現”環節關于楊輝三角的一些“秘密”而設計的一個研究性課題, 旨在探討和研究楊輝三角的性質,展現二項式系數的性質. 通過觀察、分析、猜想、證明從而發現與楊輝三角有關的數字規律.

2 解密模式

2.1 創設情境,引入課題

首先, 簡單介紹與楊輝以及楊輝三角有關的歷史故事.楊輝是我國古代數學家,其主要貢獻如圖1,出現在其著作中并注明了該圖出自北宋數學家賈憲的著作,所以“楊輝三角”實際上為“賈憲三角”. 但由于后者已失傳,故今人習慣以前者稱之.

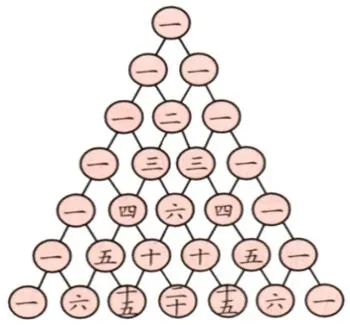
圖1 楊輝三角圖示

圖2 橫向觀察

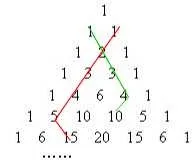
圖3 斜向觀察

通過簡要介紹楊輝三角的數學史,以數學為背景進行德育,并以此為切入點,激發學生探究楊輝三角的積極性.

2.2 合作交流,揭示性質

(1)探究楊輝三角與二項式系數的關系

計算(a+b)n(n= 0,1,2, …)展開式中的二項式系數,并將其列出,再將二項式系數與楊輝三角中的數字進行比較,嘗試發現結論: 楊輝三角的第n行是(1+1)n展開的二項式系數,即

(2)橫向觀察

注意觀察方法,即結合二項式系數,橫看、縱看、斜看,從多種角度觀察. 可得以下性質:

性質1 (對稱性)每一行中,與首末兩端“等距離”的兩項的二項式系數相等,即

性質2 楊輝三角第n行數字的和等于···+=2n.

性質3 楊輝三角的每一行中奇數項的和等于偶數項的和,即=2n-1.

(3)縱向觀察

觀察上下相鄰行數字之間的規律, 例如: 2 = 1 + 1,3=1+2,4=1+3,6=3+3,5=1+4,10=4+6……,可以得到性質4.

性質4 每一行的兩端都是1,其余每個數都等于它“肩上”兩個數的和,即

(4)斜向觀察

引導學生“斜”向觀察,例如: 1+1+1+1+1+1=6,1+2+3+4+5=15,1+3+6+10=20,1+4+10=15,歸納可得:

性質5 一般地, 在第m條斜線上(從右上到左下) 前n個數字的和, 等于第m+ 1 條斜線上的第n個數. 即

接著,我們繼續換一角度“斜”向觀察,如圖4. 進一步地,如果換個角度再次斜向觀察又會發現什么奇妙的數字特點呢? 讓學生觀察圖4 中各斜線上數字之和,算出前9 條斜線甚至更多斜線的結果.

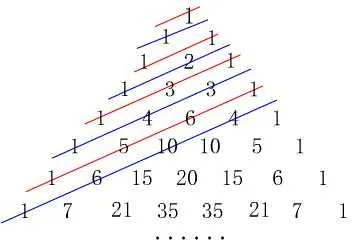
圖4 “斜”向觀察

1, 1, 2, 3, 5, 8, 13, 21, 34,···, 此數列{an}滿足an=an-1+an-2(n≥3).

性質6 從第3 條斜線起,其后各斜線上各數字的和都是前兩條斜線數字之和的和.

至此,學生在教師引導下已經完成對楊輝三角全方位的觀察,目的在于培養學生的觀察能力,以及由特殊到一般的歸納、猜想能力. 同時,在講授過程中,給學生足夠的探索時間,引導學生推廣再得出一般性的結論.

2.3 應用舉例,提升能力

如圖5 所示,在楊輝三角中,斜線上方箭頭所示的數組成一個鋸齒形的數列: 1,2,3,3,6,4,10,5,,記這個數列的前n項的和為S(n),則S(12)的值是多少?

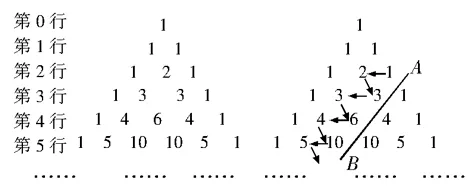
圖5 綜合觀察

通過這一思考題,讓學生學以致用的同時自我反思學習結果.

2.4 歸納小結,總結提升

本節重點在于掌握二項式系數的基本性質與楊輝三角的實際應用,同時使學生的數學思維得以提升. 但能否再繼續拓寬思維層面呢? 可以嘗試引導學生思考以下三個問題:

問題1 在楊輝三角中,除了本節課發現的性質外,你還能再找出其它的一些性質嗎? 與其他同學交流探討.

問題2 查閱有關楊輝三角與斐波那契數列實際應用的資料并與同學交流學習.

問題3 “縱橫路線圖”問題: 圖6 是X 城市的部分街道圖,

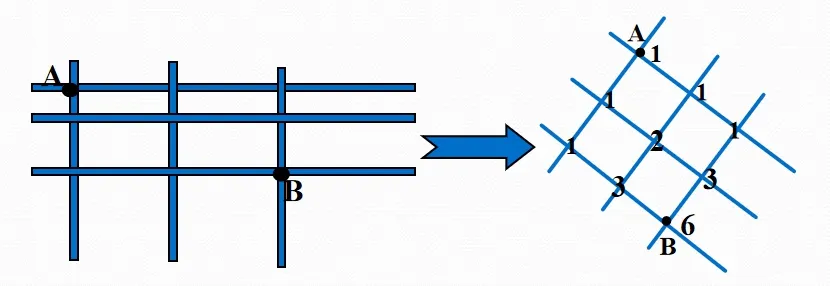
圖6 X 城市街道圖

(1)若從點A處走到點B處(注意只能由北到南,由西向東),則有幾種不同的走法? 若縱橫各四條路又有多少種走法? 有何規律?

(2)把圖順時針轉45°,如圖6 中右圖所示,在交叉點標上相應的楊輝三角數. 點B處的楊輝三角數與A到B的走法有什么關系?

最后,與學生共同總結,引導學生探究楊輝三角與斐波那契數列之間的聯系.

3 總結與啟示

HPM 視角下的二項式系數的教學是一個比較有文化味的角度,相比其他的教學視角,更具文化底蘊、歷史深度和數學思維. 這一教學實踐能為今后的高中數學教學帶來“五個一”的啟示.

一次溯源,在HPM 視角下,將學生帶回楊輝時代,想象與數學家對話,同楊輝一齊探究二項式展開式的性質,并通過數學史的學習掌握二項式展開式系數的相關性質,做到幫助學生追本溯源,真正理解概念的形成與發展,而不是僅靠死記硬背. 一種提升,通過聯系函數的圖象和相關性質探究證明二項式系數的性質,加深不同知識間的聯系,有利于幫助學生形成連貫一體的知識體系,提升對知識的把握. 一個高度,通過數形結合、歸納思想,以及教師引導、學生探究的教學方式,培養學生數學思維,促進學生學以致用,將課堂成果落實到數學思想的培養高度. 一堂德育,“楊輝三角”是我國古代數學史上重要的成就之一,彰顯了我國古代數學家的孜孜不倦和聰明才智,這一內容能讓學生認識到除了西方歐氏幾何之美,更有東方演算之美.

總而言之,數學中蘊含的美是深廣博大的,不僅有對稱美,還有簡潔美、和諧美等. 數學教學中從來不缺乏美,而是需要發現美的視角.