主動(dòng)懸架系統(tǒng)事件觸發(fā)自適應(yīng)漸近跟蹤控制

王昊宇,鄧英杰,趙丁選,?,王建濤

(1.燕山大學(xué) 機(jī)械工程學(xué)院,河北 秦皇島 066004;2.燕山大學(xué) 車(chē)輛與能源學(xué)院,河北 秦皇島 066004)

0 引言

隨著人們對(duì)車(chē)輛行駛平順性和乘坐舒適性的要求越來(lái)越高,傳統(tǒng)的被動(dòng)懸架系統(tǒng)已無(wú)法滿足這些需求。主動(dòng)懸架系統(tǒng)具有可以自適應(yīng)動(dòng)態(tài)調(diào)節(jié)剛性和阻尼特性的作動(dòng)器,可以大大提高車(chē)輛的行駛平順性和乘坐舒適性,其研究已成為近些年的熱點(diǎn)[1]。

截至目前,學(xué)者已經(jīng)提出了很多主動(dòng)懸架系統(tǒng)的控制方法,例如PID 控制[2]、自適應(yīng)控制[3]和H∞控制[4]等。文獻(xiàn)[5]在非線性模型的基礎(chǔ)上利用自適應(yīng)反步控制方法,設(shè)計(jì)了一種反步控制器,提高了列車(chē)行駛的平順性和舒適性;文獻(xiàn)[6]利用模糊控制和H∞控制,并且考慮了汽車(chē)座椅的振動(dòng),設(shè)計(jì)了一種自適應(yīng)PID 半主動(dòng)懸架控制器;龐輝等[7]在基于T-S 模糊模型的1/4 車(chē)輛懸架上應(yīng)用自適應(yīng)控制和滑模控制,通過(guò)自適應(yīng)控制降低了滑模的抖動(dòng);賈忠益等[8]針對(duì)具有控制量和輸出硬約束的不確定系統(tǒng),設(shè)計(jì)了一種具有摩擦力補(bǔ)償?shù)目刂破?文獻(xiàn)[9]為解決具有前饋控制的執(zhí)行器延遲問(wèn)題,在主動(dòng)懸架系統(tǒng)中采用了有限頻率H∞控制算法。隨著各類高精度作業(yè)對(duì)車(chē)輛位姿穩(wěn)定的需求日益苛刻,減小甚至消除主動(dòng)懸架系統(tǒng)穩(wěn)態(tài)跟蹤誤差具有重要的現(xiàn)實(shí)意義。上述文獻(xiàn)中,PID 控制算法無(wú)法嚴(yán)格證明閉環(huán)系統(tǒng)的穩(wěn)定性和跟蹤誤差的收斂性,自適應(yīng)控制算法很難解決非線性系統(tǒng)模型的不確定非線性項(xiàng),跟蹤精度不高,H∞控制算法要求線性的系統(tǒng)模型,且無(wú)法在外部激勵(lì)存在的情況下消除穩(wěn)態(tài)誤差,而針對(duì)非線性模型的基于常規(guī)反步法的控制策略,僅能實(shí)現(xiàn)跟蹤誤差的一致最終有界,跟蹤精度受調(diào)節(jié)參數(shù)影響,魯棒性差,無(wú)法解決主動(dòng)懸架系統(tǒng)在未知模型動(dòng)力學(xué)和復(fù)雜路況下的漸近高度跟蹤控制問(wèn)題。

非線性系統(tǒng)[10]在含有未知模型動(dòng)力學(xué)和環(huán)境干擾下的漸近跟蹤控制問(wèn)題是近年來(lái)控制學(xué)界關(guān)注的熱點(diǎn)。文獻(xiàn)[11]首次提出采用積分有界函數(shù)作為σ修飾的自適應(yīng)律,保證觀測(cè)誤差的漸近收斂;文獻(xiàn)[12]和[13]在嚴(yán)格反饋系統(tǒng)和非嚴(yán)格反饋系統(tǒng)的漸近跟蹤控制中應(yīng)用了積分有界函數(shù)的思想;文獻(xiàn)[14]采用Nussbaum 算子構(gòu)造控制器,根據(jù)Nussbaum 算子的有界性證明跟蹤誤差的漸近收斂。但是,目前較少有研究解決主動(dòng)懸架的漸近跟蹤控制問(wèn)題。

上述的文獻(xiàn)多采用連續(xù)型的控制策略,這就導(dǎo)致了這些控制策略的信號(hào)傳輸方式容易造成通信資源的浪費(fèi),而事件觸發(fā)控制就解決了這個(gè)問(wèn)題,即僅在采樣誤差超出設(shè)定閾值的時(shí)候才進(jìn)行信號(hào)采樣。這樣不僅具有非周期信號(hào)采樣的特點(diǎn),更符合通信受限的實(shí)際作業(yè)情況,大大減少了通信的負(fù)擔(dān),而且一定程度上保障了系統(tǒng)性能的發(fā)揮。文獻(xiàn)[15]針對(duì)具有時(shí)變?nèi)珷顟B(tài)約束的座椅系統(tǒng)和車(chē)輛電磁主動(dòng)懸架系統(tǒng),分別設(shè)計(jì)了兩種事件觸發(fā)控制器,證明了系統(tǒng)中所有的誤差信號(hào)均是有界的。將事件觸發(fā)機(jī)制應(yīng)用于主動(dòng)懸架系統(tǒng)的漸近跟蹤控制,有待探索。

針對(duì)以上問(wèn)題,本文以1/4 車(chē)輛主動(dòng)懸架系統(tǒng)的懸架高度為控制目標(biāo),設(shè)計(jì)了一種事件觸發(fā)自適應(yīng)神經(jīng)漸近跟蹤控制方案。首先對(duì)未知模型動(dòng)力學(xué)、路面輸入和虛擬控制律等采用徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)進(jìn)行逼近,提取最小學(xué)習(xí)參數(shù)并設(shè)計(jì)單參數(shù)自適應(yīng)律。然后在控制律和自適應(yīng)律的設(shè)計(jì)中采用積分有界函數(shù),設(shè)計(jì)變量事件觸發(fā)條件。最后基于Lyapunov 直接法和Barbalat 引理從理論上證明閉環(huán)系統(tǒng)的漸近穩(wěn)定性,并通過(guò)仿真驗(yàn)證控制方案的優(yōu)越性。

1 問(wèn)題表述

1.1 1/4 車(chē)輛懸架模型及數(shù)學(xué)模型

主動(dòng)懸架力學(xué)關(guān)系及變量描述如圖1。根據(jù)力學(xué)分析,1/4 車(chē)輛懸架模型的動(dòng)力學(xué)方程可描述為

圖1 二自由度1/4 車(chē)輛懸架模型Fig.1 The model of 2-degree-of-freedom quarter vehicle suspension

式中,Ft=ka(z1-z2),Fv=ca(1-2),Fw=kt(z2-zr),Fr=ct(2-r),mb是簧載質(zhì)量,mu是非簧載質(zhì)量,Fv代表阻尼力,Ft代表彈簧力,Fw代表輪胎彈簧力,Fr代表輪胎阻尼力,u代表主動(dòng)懸架系統(tǒng)的控制輸入,ka代表懸架剛度系數(shù),kt代表輪胎剛度系數(shù),ca代表懸架阻尼系數(shù),ct代表輪胎阻尼系數(shù)。

令x1=z1是車(chē)身豎直方向的位移,x2=1是車(chē)身豎直方向的速度,x3=z2是簧下豎直方向的位移,x4=2是簧下豎直方向的速度,則式(1)可表示為

控制目標(biāo):對(duì)于具有連續(xù)二階導(dǎo)數(shù)的參考信號(hào)zd(t),通過(guò)對(duì)u的控制律設(shè)計(jì)可以使z1漸近跟蹤到zd。

假設(shè)式(1)和(2)中的所有變量都定義在一個(gè)緊集中。

引理1[16]定義在緊集的任意連續(xù)函數(shù)f()都可以用徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)表示為

式中,Wf表示神經(jīng)網(wǎng)絡(luò)的權(quán)重向量,ε是以|ε|為界的近似誤差,滿足|ε|≤,?()是基函數(shù)的向量,并且滿足

引理2[12]對(duì)于任意變量s,它都滿足

式中,σ(t) 是一個(gè)正的積分有界函數(shù), 即,且> 0。

2 控制設(shè)計(jì)和穩(wěn)定性分析及其他特性證明

2.1 控制設(shè)計(jì)

定義高度跟蹤誤差

對(duì)ze求導(dǎo)可得

設(shè)計(jì)虛擬控制律

式中,kz是調(diào)節(jié)參數(shù),且kz>0。

定義跟蹤誤差

將式(8)和(9)代入式(7)可得

對(duì)式(9)求導(dǎo),并將式(2)代入可得

將式(13)代入式(12)可得

設(shè)計(jì)實(shí)控制律u,

式中,t∈(tj,tj+1],tj為事件觸發(fā)時(shí)刻,且j=1,2,…,ωr(t)是連續(xù)控制律。

定義控制誤差er(t):

設(shè)計(jì)觸發(fā)時(shí)間點(diǎn)tj和下一事件觸發(fā)時(shí)間點(diǎn)tj+1,即觸發(fā)條件為

式中,00。則u(t)可被表示為u=ωr(t)/(1+δ1ar)-δ2br/(1+δ1ar)并代入式(14)可得e=ωr(t)/[mb(1+δ1ar)]-δ2br/[mb(1+δ1ar)]+

其中,δ1∈(-1,1),δ2∈(-1,1)。

式中,βr=max{br/[mb(1-ar)]+r,‖Wr‖}且ψr=‖?r‖+1。

設(shè)計(jì)ωr(t),即

式中,kr>0 是調(diào)節(jié)參數(shù),r是βr的估計(jì)值。

式中,λr是調(diào)節(jié)參數(shù),λr>0。

2.2 穩(wěn)定性分析及其他特性證明

2.2.1 穩(wěn)定性分析

定理對(duì)于式(1)和(2)描述的車(chē)輛主動(dòng)懸架系統(tǒng),滿足假設(shè)1。如果采用式(15)的控制律,采用式(17)的觸發(fā)條件和式(22)的自適應(yīng)律,則ze和se可以實(shí)現(xiàn)漸近穩(wěn)定。

證明選取Lyapunov 函數(shù):

聯(lián)立式(11)、(21)和(23)可得

對(duì)式(25)積分,并利用引理2,可得

因此可以得出V(t)-V(0)是有界的。將式(26)移項(xiàng)整理可得

由Barbalat 引理[17]推斷式(27)中ze和se均趨向于零,證畢。

2.2.2 其他特性的證明

由上述定理證明可知se趨向于零,又由式(15)和式(20)可知,控制輸入u是有界的。[kt(z2-zr)+ct(2-r)]/mu可視為有界的外部擾動(dòng)。而式(29)是一個(gè)經(jīng)典的二階阻尼系統(tǒng),所以z1-z2和1-2是有界的,因此,式(28)中1最終可以收斂到一個(gè)有限值,這意味著可以達(dá)到穩(wěn)定乘坐舒適性的效果。

根據(jù)圖1,車(chē)輛的路面附著力與地面支持力有關(guān),而地面支持力由Fw和Fr所控制。因此分別在式(2)中等式的兩邊減去r,可得

3 仿真驗(yàn)證

為驗(yàn)證針對(duì)1/4 車(chē)輛懸架模型提出的控制方法的有效性,分別選擇以下參數(shù):

路面的擾動(dòng)信號(hào)設(shè)置為

徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)采用11 個(gè)神經(jīng)元,控制參數(shù)設(shè)置為kz=5,kr=2,ar=br=0.2,λr=0.5,其中積分有界函數(shù)設(shè)置為σr=0.3exp(-0.02t)。仿真時(shí)間設(shè)置為10 s。

為驗(yàn)證控制策略的優(yōu)越性,以魯棒阻尼策略[18]為例進(jìn)行對(duì)比。魯棒阻尼策略的控制律設(shè)置:

其中,控制參數(shù)和上述保持相同。仿真結(jié)果如下所示。

圖2 和圖3 展示了懸架高度z1和輪胎高度z2在兩種控制策略之下的軌跡變化,可以發(fā)現(xiàn):本文提出的漸近跟蹤控制策略相比魯棒阻尼策略明顯具有更高的跟蹤精度,可以更快地實(shí)現(xiàn)跟蹤誤差的收斂。圖4 給出了本文控制策略中自適應(yīng)參數(shù)r的演變過(guò)程,可以看出直接自適應(yīng)控制的設(shè)計(jì)使r最終趨向于穩(wěn)定且有界。圖5 對(duì)比了兩種控制策略下的控制輸入,對(duì)比發(fā)現(xiàn)本文的控制策略比魯棒阻尼策略更具有顯著的效果,收斂速度更快。圖6 給出了本文控制策略下事件觸發(fā)間隔時(shí)間的變化,該策略共有128 個(gè)觸發(fā)時(shí)刻,最長(zhǎng)的觸發(fā)間隔時(shí)間為0.93 s,最短的觸發(fā)間隔為0.01 s。相比之下,魯棒阻尼策略的信號(hào)采樣周期為0.01 s,共有1 001 個(gè)采樣次數(shù)。因此,本文所采用的事件觸發(fā)控制可明顯地在控制器至執(zhí)行器通道上節(jié)省通信資源。

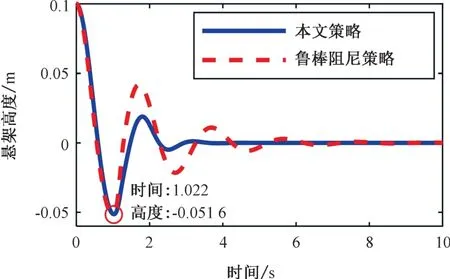
圖2 兩種控制策略的懸架高度對(duì)比Fig.2 Comparison of suspension heigh between the two control strategies

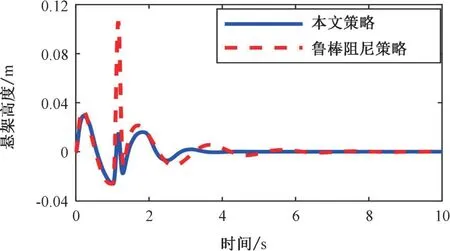
圖3 兩種控制策略的輪胎高度對(duì)比Fig.3 Comparison of tire heigh between the two control strategies

圖4 自適應(yīng)參數(shù)的變化Fig.4 Change in adaptive parameter

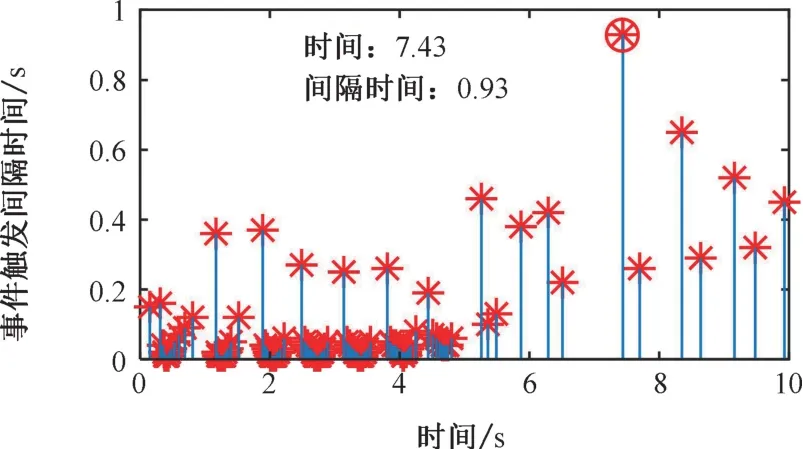
圖6 本文策略下的觸發(fā)時(shí)間間隔Fig.6 Inter-event time in the proposed scheme

4 結(jié)論

本文提出了一種主動(dòng)懸架系統(tǒng)的事件觸發(fā)自適應(yīng)神經(jīng)漸近高度跟蹤控制方案,利用了徑向基函數(shù)神經(jīng)網(wǎng)絡(luò)、最小學(xué)習(xí)參數(shù)化技術(shù)和積分有界函數(shù)等,并通過(guò)仿真試驗(yàn)驗(yàn)證了其優(yōu)越性,以下為該方案的優(yōu)點(diǎn):

1)實(shí)現(xiàn)了對(duì)未知模型動(dòng)力學(xué)和路面輸入雙重作用下主動(dòng)懸架跟蹤誤差的漸近收斂,滿足了車(chē)輛行駛平穩(wěn)性所需的高精度要求;

2)采用最小學(xué)習(xí)參數(shù)化技術(shù)構(gòu)造了單參數(shù)自適應(yīng)律,確保了控制策略的計(jì)算簡(jiǎn)便性;

3)事件觸發(fā)控制的設(shè)計(jì)減少了控制器至執(zhí)行器通道上信號(hào)的采樣頻率,可以有效地節(jié)省通信資源。

本文所提出的方案并不局限于1/4 車(chē)輛懸架系統(tǒng)的高度跟蹤控制,也可以根據(jù)相同設(shè)計(jì)思路應(yīng)用拓展到半車(chē)模型乃至整車(chē)模型的主動(dòng)懸架的高度跟蹤控制。