基于流固耦合的航空導葉作動筒振動特性分析

曹 洋,王澤坤,劉鵬舉,趙 振,孔祥龍,滿春雷,姚 靜

(1.中國航發長春控制科技有限公司,吉林 長春 130102;2.燕山大學 機械工程學院,河北 秦皇島 066004;3.燕山大學 河北省輕質結構裝備設計與工藝工程技術創新中心,河北 秦皇島 066004;4.空裝駐長春地區軍事代表室,吉林 長春 130102)

0 引言

航空航天產品的工作環境惡劣,因而對其性能也有嚴格要求,高壓壓氣機在工作時具有高溫、高壓、高速和變載荷的特點[1],會產生各種形式的劇烈振動。其內部的導葉作動筒是控制高壓壓氣機導葉動作的重要構件,各種振動沖擊的工作環境使導葉作動筒本身產生復雜的振動響應[2]。因此需要對作動筒工作時的固有動態特性進行更為準確和全面的研究,保證其使用過程中的可靠性,避免安全事故和經濟損失。

針對航空發動機工作過程中的振動問題,文獻[3]研究了航空發動機壓氣機葉-盤耦合的振動特性,得到了離心載荷對頻率和振型的影響規律。文獻[4]研究了航空發動機葉片的動態響應特性,發現高速振動情況下葉片模態振型與應力具有相對穩定性。針對作動筒結構的振動問題,文獻[5]利用UG 軟件對某發動機放氣作動筒進行了仿真建模,研究主要失效和破損位置。文獻[6]對一種起落架作動筒進行了靜力學和動力學仿真建模,并依據仿真結果對作動筒進行了優化設計。文獻[7]基于正弦振動的疲勞仿真,結合試驗結果對某型作動器進行結構優化來避免結構斷裂。

目前對于航空導葉作動筒的研究主要集中在液壓伺服控制,而流固耦合的非線性結構振動方面的研究較少。本文基于某航空導葉作動筒的實際工況并考慮內部油液質量與壓力影響,建立流固耦合動力學模型,研究接觸剛度對可動副自由度的影響機制,分析接觸位置及接觸狀態對固有頻率的影響;通過共振檢查試驗驗證仿真模型的準確性,根據《機載設備環境條件及試驗方法-振動》[8]建立隨機振動仿真模型,分析零部件的應力和變形情況,為其故障檢測與結構優化提供依據。

1 作動筒工作原理及主體結構

航空發動機內高壓壓氣機導葉作動筒的工作原理如圖1 所示。其連接座底部軸承用于固定作動筒,活塞桿端軸承用于輸出作動筒位移,筒體內部集成的線位移傳感器通過螺釘固定于連接座,活塞與活塞游標及桿端軸承組件固定共同運動,線位移傳感器通過檢測活塞游標的相對位移來反饋作動筒當前的運動狀態。通過電液伺服閥控制作動筒有桿腔與無桿腔的油液流量來調節活塞的伸縮位置。活塞桿端軸承與葉片通過連桿鉸接在一起,通過活塞位移改變壓氣機葉片空間角度,從而調節航空發動機內外涵道進氣量[9],保證航空發動機穩定工作。

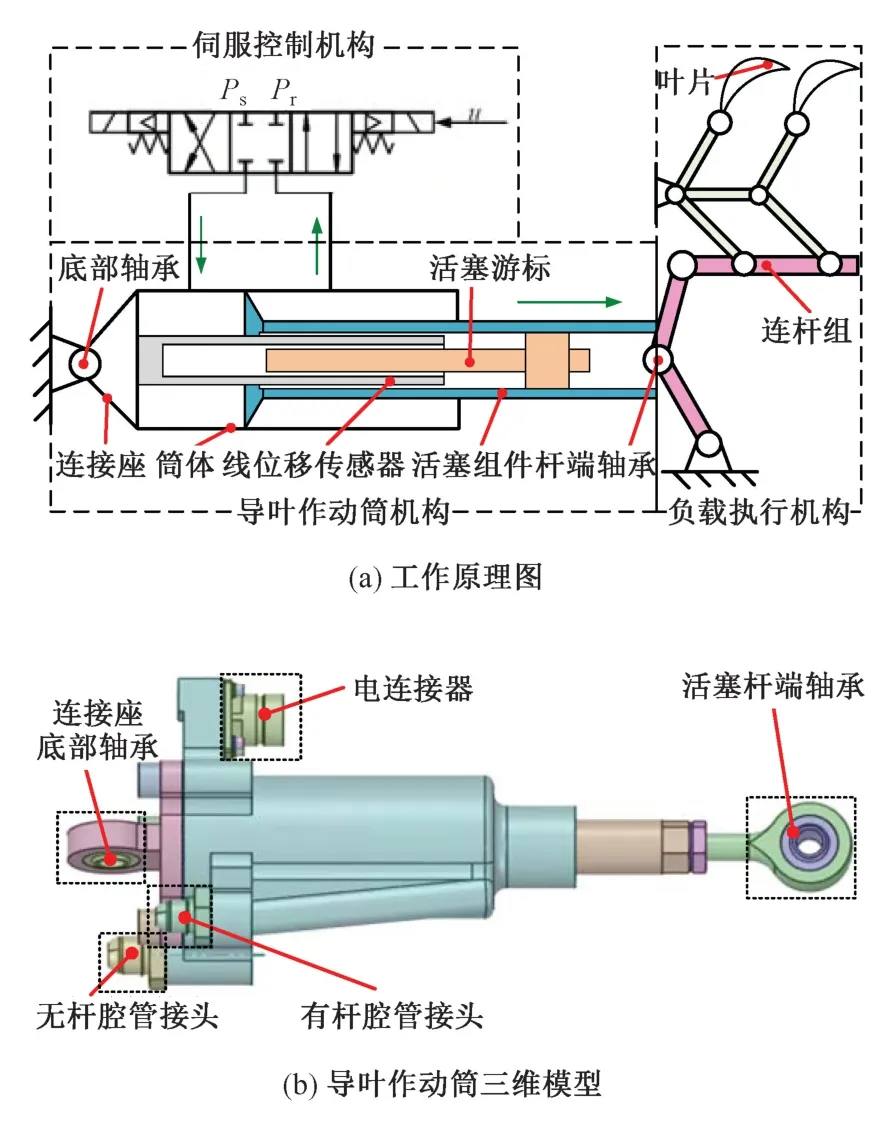
圖1 某型作動筒工作原理圖Fig.1 Working principle diagram of a type of actuating cylinder

2 作動筒靜力學分析

2.1 工裝-作動筒三維有限元模型

首先建立作動筒的材料庫模型,依據航空材料手冊、標準件相關標準等查取相應材料的力學參數,主要部件材料的力學參數如表1 所示。

表1 材料力學參數Tab.1 Mechanical parameters of material

考慮到振動試驗時工裝結構的質量和連接剛度對固有頻率的影響[10],在原有作動筒模型及試驗坐標基礎上,進行工裝建模并與作動筒組合裝配,建立工裝-作動筒的幾何模型。

為得到作動筒真實的固有振動特性,還需要考慮零組件間各種接觸行為,在該模型中存在兩種需要特殊處理的接觸,一種涉及到間隙接觸的處理,該種接觸面之間存在小間隙,通過調整球形域、滲透容差等調整接觸探測范圍,保證接觸探測范圍覆蓋接觸間隙;另一種需特殊處理的接觸涉及局部自由度的處理,主要集中在活塞與筒體的接觸位置,為保證在進行模態仿真計算時保留活塞在結構中的局部自由度,對相關接觸類型和接觸剛度進行了調節。另外在作動筒與工裝連接的位置,將關節與接觸結合使用,保證了合理的連接剛度,避免過約束的現象。針對各個零部件進行合理網格劃分與調整,建立工裝-作動筒三維有限元模型,如圖2 所示。

圖2 工裝-作動筒三維有限元模型Fig.2 Fixture-actuating cylinder 3D finite element model

2.2 預緊力邊界條件

作動筒各零組件間主要通過螺釘相互連接,螺釘預緊力會改變連接件間的接觸剛度,影響固有頻率。作動筒的螺釘分布在連接座與筒體之間、連接座與電連接器之間、連接座與線位移傳感器之間,對各型號螺釘所需施加預緊力進行計算。

對螺釘公稱應力截面積As進行計算:

式中,As為螺釘公稱應力截面積,d2為螺釘外螺紋中徑,d3為螺紋計算直徑。

對螺紋計算直徑d3進行計算:

式中,d1為螺釘外螺紋小徑,H為螺釘螺紋的原始三角形高度。

預緊力F′的計算公式為

式中,σs為螺釘材料的屈服點。

計算并取整后得到各螺釘的預緊力,螺釘材料的屈服強度與最終施加預緊力如表2 所示,在仿真模型中對實體螺釘加載預緊力邊界條件。

表2 螺釘材料的強度Tab.2 Material strength of screws

2.3 流固耦合仿真模型

仿真模型考慮了作動筒中油液的影響,涉及到油液質量和油液壓力的處理。使用的油液為GJB 1263—1991 航空3 號噴氣燃料,其密度為780 kg·m-3,運動粘度為1.25 mm2·s-1。對筒體內空腔進行流道抽取,借助Fluent 平臺進行流固耦合計算,得到流體壁面的壓力分布[11]。通過等效質量法,將流體質量附加在筒體上[12]。等效計算式為

式中,ρ為固體等效密度,ρG為固體密度,ρL為流體密度,VG為固體體積,VL為流體體積。

通過流固耦合仿真模型計算油液壓力分布,引入作動筒受油液壓力的邊界條件,在Fluent 中對流域給定壓力邊界條件,入口為12 MPa 壓力邊界,出口為0.2 MPa 壓力邊界,對仿真模型進行壓力分布計算,結果顯示有桿腔油壓分布12 MPa,無桿腔油壓分布0.2 MPa,如圖3 所示。

圖3 油液流體仿真模型Fig.3 Oil fluid simulation model

將油液壓力分布引入靜力學模型,給定固定邊界條件,對流固耦合仿真模型進行有限元仿真計算, 計算結果顯示螺釘位置應力最大為187 MPa,低于螺釘材料屈服強度,計算得到筒體的應力分布結果,最大應力為153 MPa,遠小于筒體材料的屈服強度 ( 筒體的材料為0Cr17Ni4Cu4Nb,筒體工作溫度在200 ℃以下,該材料在該溫度下屈服強度超過1 180 MPa),如圖4所示。靜力學分析引入了預緊力與油液壓力分布兩種邊界條件,并給定固定邊界設置,獲得了受力位置的應力結果,為后續仿真奠定基礎。

圖4 靜力學應力分布Fig.4 Static stress distribution

3 作動筒模態分析

3.1 接觸剛度因子對活塞扭振頻率的影響

理論上作動筒的活塞存在沿行程方向上的移動自由度以及繞軸心扭轉的自由度,純剛性連接會導致過大結構剛度,無法釋放正確的局部自由度振型,為正確映射活塞可移動件的自由度情況,現通過相關接觸參數調整以保證活塞產生這兩種振型。

在筒體和活塞之間使用不分離接觸和無摩擦接觸,為避免出現較大接觸穿透,調節3 個關鍵接觸的接觸剛度因子,如圖5 所示。接觸剛度因子越大兩接觸面之間的接觸剛度越大,接觸面之間更不易計算穿透,會影響相應位置的結構剛度,在一定程度上改變模態振型和固有頻率。通過改變接觸剛度因子進行多組仿真,總結出相關接觸設置不同接觸剛度因子時活塞扭振的固有頻率,如圖6 所示。發現接觸剛度因子低于0.8 時相關固有頻率受其影響很大,但在接觸剛度因子達到0.8以后相關固有頻率趨于穩定,且從振型上看無較大計算穿透現象,因此這3 個接觸的接觸剛度因子設定為0.8。

圖5 調節接觸剛度因子的接觸Fig.5 Contacts of adjusting contact stiffness factor

圖6 接觸剛度因子對固有頻率影響Fig.6 The influence of contact stiffness factor on nature frequency

3.2 模態仿真結果

以靜力學分析結果引入邊界條件作為初始條件計算作動筒的固有頻率及振型,考慮后續仿真工作要求,模態分析的頻率范圍應大于正弦振動分析頻率的1.5 倍,因此設置仿真計算頻率范圍為0～3 000 Hz。模態計算得到作動筒在2 000 Hz以下的8 階固有頻率,如表3 所示,前三階振型如圖7 所示。

表3 作動筒固有頻率Tab.3 Natural frequency of actuator cylinder

圖7 作動筒前三階模態振型Fig.7 The first three modal shapes of the actuator cylinder

從振型來看,前三階振型的振動趨勢主要發生在筒體、活塞桿、軸承固定位置和電連接器附近,剛度上主要涉及到活塞桿抗彎剛度與筒體的抗扭剛度,第四階振型及以后的振動趨勢主要和電連接器附近的局部振動有關,因此有一定誤差。此有限元模型獲取了該型作動筒在實際工況下的動態響應,工作時避免固有頻率可提高使用壽命。該作動筒有限元模型中對活塞局部自由度的調節方法,可指導存在局部自由度的作動筒類結構組件進行振動仿真建模。

3.3 不同行程位置下的固有頻率變化規律

仿真計算可獲取試驗無法檢測位置的響應信息,比如作動筒內部無法通過傳感器探測到的位置的響應信息,還可以在保證仿真模型正確的基礎上,進行更多組次不同變量的仿真計算,其效率和成本問題都優于試驗。因此對作動筒的活塞在不同行程位置時的工況進行多組仿真,獲取其振型與固有頻率變化規律。

作動筒在調節葉片角度時,活塞在行程上的位置會發生改變,因此針對活塞在不同行程位置時的作動筒進行了模態仿真分析。活塞底部距離筒腔底部的距離為S,如圖8 所示,研究活塞距筒底距離S為0 mm、15 mm、30 mm 與45 mm 位置時的前四階固有頻率變化規律。隨著活塞在行程上位移變大,前四階固有頻率都有降低的趨勢,但第一階與第四階固有頻率變化較小,其中第一階固有頻率主要涉及筒體的抗扭剛度,第二、三階固有頻率主要涉及作動筒的抗彎剛度,第四階固有頻率主要涉及活塞的抗扭剛度,在活塞移動過程中作動筒的抗扭剛度變化較小,因而不同活塞位置下第一、四階固有頻率相差較小,抗彎剛度變化相對較大,因而不同位置下第二、三階固有頻率相差較多,活塞在不同行程位置下的各階振型都相同,如圖9 所示。

圖8 活塞行程位置Fig.8 The piston stroke position

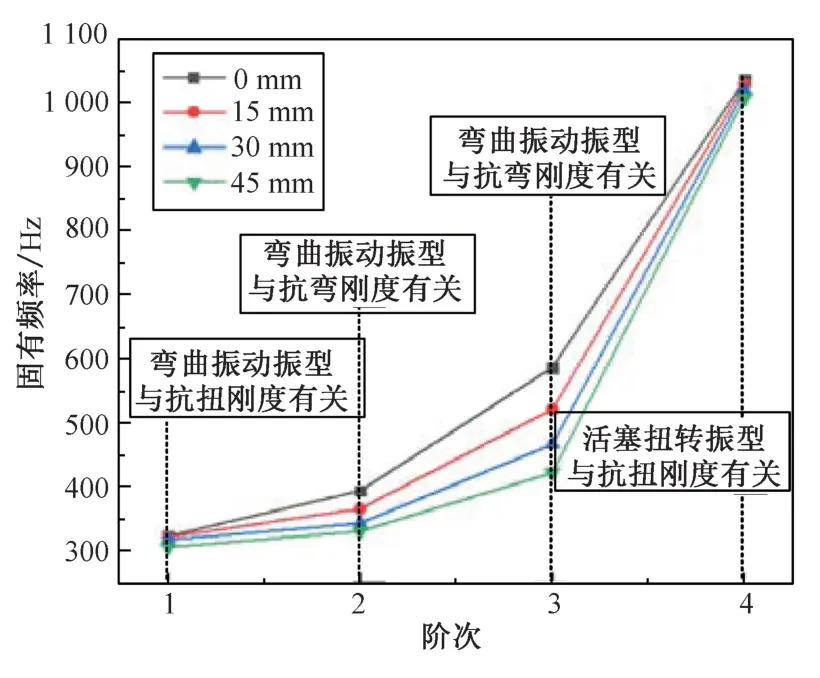
圖9 不同活塞位置下的前四階固有頻率Fig.9 The first four natural frequencies at different piston positions

3.4 濕模態模型下的油液振型

基于Fluent 建立流固耦合模型下的模態仿真模型無法觀察油液振型,因此建立濕模態仿真分析模型,對作動筒振型進行求解,獲得了包含油液振型在內的作動筒振型。濕模態仿真可保留油液模型,因此不需要用式(4)將油液質量等效到筒體上。提取油液的前三階模態振型,如圖10 所示。

4 作動筒共振檢查試驗

4.1 共振檢查試驗方法

依靠振動試驗臺施加的正弦激勵產生振動環境,在0～2 000 Hz 頻率范圍內對作動筒進行共振檢查試驗,搜集作動筒在工作狀態下產生響應峰值的共振頻率。根據機載設備環境條件及試驗方法-振動(HB 5830.5—1984)規定的加速度及位移載荷:頻率在10～40 Hz 內,施加0.3 mm 的位移振幅載荷;頻率在40 Hz 以上時,施加2g的加速度載荷進行共振檢查試驗。

模擬活塞位于0 mm 位置的工作初始狀態,通過工裝上的銷軸與兩端軸承連接,將其安裝在振動試驗臺上。試驗時腔體內充滿油液,無桿腔油壓保持0.2 MPa,有桿腔油壓保持12 MPa,依靠油液壓差使活塞組件保持在0 mm 位移位置。考慮到作動筒結構在低頻段不易發生沿活塞軸向的振動,因此通過振動試驗臺提供沿y軸和z軸正方向的正弦激勵載荷,在連接座附近位置安裝加速度傳感器并輸出加速度響應信號。

4.2 試驗響應結果

安裝就緒后進行作動筒共振檢查試驗,通過共振檢查試驗得到作動筒沿y軸和z軸的幅值比響應曲線,如圖11 所示,根據響應結果,提取響應幅值比大于1 的峰值點對應的頻率,視作試驗過程中獲得的共振頻率點,將頻率值由小到大排序,得到作動筒前六階共振頻率,如表4 所示。

表4 沿y 和z 向前三階響應結果Tab.4 The first three order response along y and z

圖11 作動筒響應曲線Fig.11 Response curve of actuator cylinder

以試驗坐標系為基準,在仿真模型中通過作動筒各階振型沿三軸方向的有效參與質量確定沿y和z方向的前三階固有頻率,并將模態仿真得到的固有頻率與共振檢查試驗結果進行對比,計算仿真獲取固有頻率的誤差。

對仿真獲取的固有頻率進行相對誤差計算:

式中,δ為相對誤差,f1為仿真獲取的固有頻率,f2為試驗獲取的固有頻率。

通過計算得到的誤差分布發現,1 000 Hz 以下固有頻率的仿真誤差均不超過2%,其余固有頻率的誤差也保持在10%以下,如圖12 所示,驗證了所建立非線性模態仿真模型的準確性,可用于后續仿真研究。

圖12 仿真固有頻率與試驗數據對比Fig.12 Comparison of simulated natural frequencies and experimental data

5 作動筒隨機振動分析

5.1 隨機振動分析基本原理

隨機振動分析主要從統計學出發,得到對象在隨機載荷下的結構響應,由于多數隨機載荷無法直接量化,一般通過功率譜密度函數描述,使用激勵的均方值與頻率帶寬的比值評估,激勵載荷可以為加速度激勵、速度激勵以及位移激勵[13]。

功率譜密度函數定義為

式中,Sy(ω)為功率譜密度函數,Ry(τ)為功率譜密度函數在時域內的自相關函數。

假設單一輸入的功率譜密度函數矩陣為Sx(ω),則得到的響應功率譜密度函數Sy(ω)為

式中,H(ω)為運動系統的頻率響應矩陣,與系統的動力學微分方程有關。即輸入多個功率譜密度函數以及由模態分析得到的固有頻率和振型,可輸出結構在不同置信度下的應力和變形結果以及測點在軸線方向上的響應譜曲線。

5.2 隨機振動仿真分析

在模態分析的基礎上進行隨機振動分析,依據機載設備環境條件及試驗方法-振動(HB 5830.5—1984)選擇標準的隨機振動載荷功率譜,如圖13 所示,提取功率譜節點具體參數值,如表5 所示,將功率譜輸入到仿真模型進行計算。

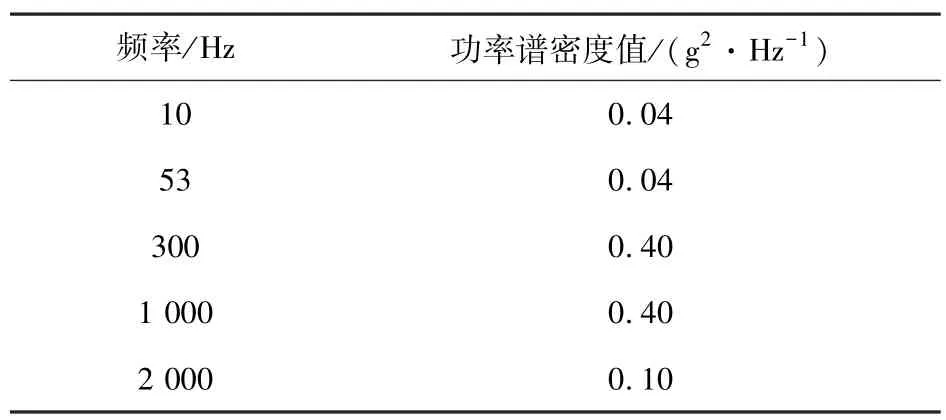
表5 功率譜密度參數值Tab.5 Power spectrum density parameter value

圖13 功率譜密度函數Fig.13 Power spectral density function

考慮到作動筒的結構及工作特性,重點研究連接件及工作部件的隨機振動響應。采用Segalman-Fulcher 方法計算活塞及連接座兩個元件沿y軸正向在3σ(該算法中代表結構Von Mises應力的3 倍均方根值)下的等效應力。隨機振動的輸入和輸出均為統計數據,根據Von Mises 應力準則和實際概率分布進行強度評估,當3σ等效應力大于材料許用應力時,結構將發生破壞。

通過比較三個軸向的計算結果,可知連接座最大變形量不超過0.33 mm 的概率為99.73%(變形響應中3σ為99.73%的置信區間),位于連接座與筒體接觸連接的區域。活塞最大變形量不超過0.69 mm 的概率為99.73%,位于活塞尾部區域。連接座最大應力響應為222.0 MPa,位于直角過渡區域;活塞最大應力響應為257.2 MPa,位于與筒體接觸連接的區域,如圖14 所示,活塞與連接座產生的應力值小于二者材料的屈服強度(活塞與連接座的材料均為0Cr17Ni4Cu4Nb),但發生了應力集中現象,可對這些位置的結構尺寸進行優化。

圖14 關鍵元件在3σ 下的變形及等效應力云圖Fig.14 Nephogram of deformation and equivalent stress of key parts under 3σ

連接座是作動筒重要的連接零件,其吊耳底部容易產生應力集中的現象,建議在該部位增加加強筋、增加吊耳厚度尺寸或大角度過渡直角等結構改進方式。活塞在作動筒工作過程中是主要的移動零件,且活塞在行程上位移越大,振動時受到應力越大,可在保證總體質量的情況下適當增加該位置壁厚,以保證作動筒工作時的穩定性和使用壽命。

6 結論

1) 在仿真建模過程中綜合考慮了多因素影響,利用單一變量法研究了活塞位置接觸剛度因子對活塞局部自由度振型的影響規律,發現相關接觸的接觸剛度因子合理值為0.8。基于流固耦合建立的非線性模態分析仿真模型獲得了導葉作動筒固有頻率與振型,從振型中發現振動趨勢最大的位置在活塞桿和電連接器附近。

2) 完成共振檢查試驗并驗證了非線性模態分析仿真模型的準確性。利用該仿真模型對活塞處于不同行程位置時的工況進行多組仿真,對比前四階固有頻率和振型,發現不同工況下前四階振型相同,但第二、三階固有頻率變化較為顯著,說明隨著活塞位置改變,導葉作動筒的抗彎剛度發生較大改變,而抗扭剛度變化較小。

3) 在模態結果基礎上對作動筒進行隨機振動仿真分析,提取到活塞及連接座兩個關鍵元件在3σ下的應力及變形響應,獲得了關鍵零件的應力集中位置,給出了在連接座和活塞桿位置的結構優化建議,有利于提高作動筒的工作壽命和可靠性。