非均勻加熱工況高溫平板熱管的穩態性能研究

于蓮韻,楊 夷

(中國原子能科學研究院 反應堆工程技術研究所,北京 102413)

高溫熱管結構簡單、傳熱系數大、等溫性良好,可以滿足特種核動力電源[1-3]、航空航天熱防護[4]等特殊領域高熱流密度的輸熱和散熱需求。對于熱管冷卻式反應堆,常規熱管蒸發段受形狀限制無法與燃料元件緊密貼合,其接觸熱阻很難在異種材料大徑向溫度梯度條件下維持穩定。目前,較大功率(MW級)反應堆需在堆芯布置上千根高溫熱管。在堆芯空間受限的條件下,結構排布的難度增加,成型質量也難以保證。外形呈平板狀,內部由數個互相獨立的熱管單元形成熱管簇的高溫平板熱管陣列(熱板)與板式燃料元件緊密貼合,有望解決常規熱管接觸面積小、接觸熱阻大、安裝復雜等問題,且每個換熱單元獨立運行,單腔失效或意外過熱不會對整體結構造成致命影響,提高了熱板整體的可靠性。平板熱管已應用于電子器件散熱、高速飛行翼面熱疏導[5]等領域。

國內外研究人員對平板熱管展開了大量的實驗研究,探究了吸液芯結構[6]、傾斜角[7]、充液率[8]、加熱方式[9]等因素對平板熱管啟動和運行性能的影響;建立了多種適用模型,以研究平板熱管內部工質的流動傳熱特性,如Faghri等[10]從熱力學循環角度建立了熱管二維熱阻網絡模型,Aghvami等[11]開發了簡化的二維數值模型分析不同加熱和冷卻配置下平板熱管的溫度壓力分布和毛細極限,Vadakkan等[12]開發了三維數值模型來研究具有多個離散熱源的扁平熱管的性能,李時娟等[13]基于液體飽和度和多孔毛細力的關系建立了毛細芯平板熱管的流動傳熱模型并計算其最大傳熱能力。對平板熱管的研究多集中于中低溫范圍,對高溫平板熱管尤其是極端非均勻熱流載荷下熱管運行性能的研究極少。而非均勻加熱普遍存在于實際的堆芯換熱中,同時,高熱流密度下高溫熱管依靠常規吸液芯回流的液體難以滿足蒸發段蒸發量,導致熱管無法穩定工作甚至燒毀。因此,平板熱管在非均勻高熱流輸入工況的運行性能決定了其能否適用于冷卻堆芯。

本文針對平板熱管陣列的特征單元,基于有限元軟件COMSOL開發平板熱管三維熱-流-固耦合分析模型,設計一種含異型干道的復合吸液芯結構,分析非均勻加熱對平板熱管內部流動、傳熱性能、力學性能的影響,初步驗證平板熱管用于堆芯冷卻的可行性。本研究建立的分析方法也可為異型熱管特殊工況下的性能評價和結構優化提供參考。

1 平板熱管結構模型

圖1為平板熱管陣列內部特征單元的結構示意圖,整個平板熱管陣列可看成是一系列該熱管單元并聯,整體結構為一體化成型,各單元之間無縫連接,故以該最小單元為研究對象來分析預測平板熱管陣列的運行性能,可將其視為左右兩側絕熱的平板熱管。熱管內部布置了干道式復合吸液芯結構以減小液體回流阻力;外層金屬絲網吸液芯緊附矩形殼體,內層吸液芯呈跑道形,吸液芯間隙自然形成4個方圓角型干道結構。蒸汽在跑道形吸液芯圍成的空腔中流動,液體在復合吸液芯內回流,實現工質循環。

圖1 平板熱管結構

考慮熱管工作溫度(750～800 ℃)及材料的相容性,工作流體選擇高純鈉,吸液芯為300目316L不銹鋼絲網,殼體及端蓋材料為Inconel 718。結構參數列于表1。

2 數值模型及方法

2.1 基本假設

根據平板熱管實際工作特性[14],作如下假設:1) 熱管工作處于穩態,氣液平衡;2) 蒸汽為可壓縮層流,液體為不可壓縮層流;3) 蒸汽腔內氣體符合理想氣體假設;4) 吸液芯內充滿過冷液體,不考慮氣泡成核、沸騰等過程,不存在干燒;5) 蒸汽腔只被蒸汽填充,吸液芯只被液體填充,吸液芯上工質的蒸發冷凝發生在氣液界面;6) 吸液芯層等效為各向同性、均質的多孔介質進行流動和傳熱分析;7) 除蒸汽密度外,蒸汽、液體、吸液芯及管壁的物性參數隨溫度變化[15-16]。

2.2 控制方程及邊界條件

對蒸汽腔、吸液芯、干道和管壁建立統一的守恒方程。

k相的質量守恒方程為:

(1)

k相的動量守恒方程為:

(2)

式中:k=l,g分別為液相或氣相;ρk為工質密度;pk為工質壓力;μk為工質動力黏度;Vk為工質流動速度;CEk為慣性阻力系數;εk為孔隙率;Kk為滲透率。

對于蒸汽腔和干道,ε=1,K=∞;對于吸液芯,孔隙率和滲透率的計算式為:

(3)

(4)

式中,N為絲網目數。

能量守恒方程為:

(5)

式中:T為溫度;V為流速;ρ為密度;cp為比定壓熱容;(ρcp)eff和keff為各部分的等效熱容和等效熱導率。

對于蒸汽腔、干道和管壁,有:

(ρcp)eff=(ρcp)i

(6)

keff=ki

(7)

式中,i=g,l,s分別為氣相、液相、固相。

對于吸液芯,等效熱容為:

(ρcp)eff=(1-ε)(ρcp)s+ε(ρcp)l

(8)

等效熱導率由Chi等[17]提出的公式計算:

(9)

分區域獨立計算蒸汽和液體的流動,通過在氣液界面上添加邊界條件,代替各區域內相變引起的質量遷移。

氣液界面兩相處于平衡狀態,飽和蒸汽壓隨溫度的升高而升高,驅動腔內蒸汽從高溫區流向低溫區。對蒸汽區,將氣液界面設為壓力入口邊界,端部為無滑移邊界。工質鈉飽和蒸汽壓與溫度的關系由Browning和Potter給出的方程[18]確定,與Clausius-Clapeyron關系式[19]相比,更接近現有實驗數據[20]。計算式為:

(10)

式中:p為壓力,MPa;T=864～2 599 K。

氣液界面處發生蒸發冷凝相變,引起的質量遷移為:

mv=ρgVgAg=ml=ρlVlAl

(11)

發生相變的氣液流通面積相等,則界面兩側蒸汽和液體流速的關系為:

(12)

對液體區(包含吸液芯和干道),設定氣液界面為如上速度入口邊界。

熱管內的傳熱過程相互影響,氣液界面的熱邊界條件由相間熱交換動態決定,采用整場耦合的方法求解。為模擬相變引起的氣化潛熱能量遷移,在氣液界面處添加熱源,界面處的能量遷移q為:

(13)

取指向氣體側的速度方向為正,則在蒸發段,q>0;在冷凝段,q<0。

平板熱管單元只在上下兩個壁面加熱或冷卻,左右壁面和端部視為絕熱,邊界條件列于表2。表2中:kw為壁面熱導率;q為熱流通量;h為冷凝段對流換熱系數;T∞為冷凝段邊界換熱溫度;Twick為吸液芯溫度;σ為發射率;ε為黑體輻射系數;n為界面法向方向。

表2 平板熱管模型的邊界條件

2.3 模型精度驗證

基于上述數學物理模型,采用COMSOL Multiphysics 6.0軟件對平板熱管模型進行建模求解。采用了軟件內置的層流模塊、Brinkman方程模塊和多孔介質傳熱模塊,整場離散、整場求解[21]的方式耦合求解平板熱管內部的流動換熱特性。

通過計算文獻[22]中方形鈉熱管的參數,并將計算結果與其中實驗數據、熱阻網絡法模型和CFD計算結果進行對比,驗證數值模型的精度。實驗中采用的方形鈉熱管長度為400 mm,寬度和高度為12.54 mm,蒸發段為150 mm,冷凝段為50 mm,壁厚為1.6 mm,吸液芯厚度為1 mm。在蒸發段加熱功率為600 W時,方形熱管軸向上壁溫的實驗測量值和模擬值的比較如圖2所示。實驗數據中冷凝段末端溫度突降,原因是熱管內有不凝性氣體。忽略該數據點,本文模型與文獻中兩種模型計算的模擬值相比,較接近實驗數據,最大相對誤差為0.95%,證實了該數值模型模擬非常規截面型熱管傳熱過程的準確性。

采用Tien等[23]數據驗證數值模型計算熱管內蒸汽流動的精度。文獻中鈉熱管總長為600 mm,蒸發段長度為200 mm,冷凝段長度為300 mm,蒸汽通道直徑為17.2 mm。功率為1 245 W時,熱管中心線蒸汽沿軸向的溫度和壓降分布如圖3所示。由圖3可看出,計算值與文獻參考值的符合性良好,溫度和壓降的最大誤差分別為4 ℃和53 Pa,變化趨勢一致,可以準確模擬熱管內部的流場特性。

圖3 熱管蒸汽中心軸向溫度與壓降分布

綜上,該模型可用于分析平板熱管穩態運行的性能。

2.4 計算方法及有限元模型

為分析非均勻加熱對平板熱管性能的影響,將殼體的固體力學模型和以上模型耦合建立三維熱-流-固模型,計算流程如圖4所示。熱應力計算中給定位移約束,上表面z方向的位移約束為0,xy平面可以做微小形變。

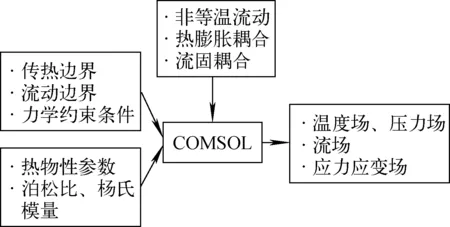
圖4 熱流固耦合計算流程

平板熱管結構對稱,選取1/2熱管進行有限元建模,采用自由四邊形網格對模型進行劃分。經網格無關性驗證,在考慮計算精度和效率的基礎上,采用如圖5所示的網格劃分。

3 結果分析

基于平板熱管三維熱-流-固耦合分析模型,計算給定加熱功率下平板熱管穩態運行時的相關熱工參數,驗證干道式復合吸液芯結構設計的合理性。

定義加熱不均勻度:

(14)

式中:QT為蒸發段上壁面加熱功率;QB為蒸發段下壁面加熱功率;Q=QT+QB為總加熱功率。

總加熱功率不變,蒸發段上下壁面加載不同功率,分析加熱不均勻度對平板熱管溫度分布等熱工參數和熱應力分布的影響。

3.1 吸液芯結構對平板熱管性能的影響

無干道平板熱管采用覆蓋管壁的金屬絲網吸液芯,本文設計的平板熱管采用干道式復合吸液芯;兩者蒸汽腔體積相同。圖6示出了總加熱功率為4 000 W(均勻加熱)時,兩種熱管蒸汽腔內氣相和吸液芯內液相在氣液界面處的相對壓力分布,以冷凝段末端為壓力參考點。由圖6a可看出,兩者蒸汽壓力的變化具有一致性:在蒸發段呈拋物線分布,在絕熱段因摩擦阻力線性降低,在冷凝段因蒸汽流速下降而回升。吸液芯的結構變化對蒸汽的流動基本無影響。干道式平板熱管的蒸發段蒸汽壓降偏大,可能破壞熱管軸向的均溫性。由計算得兩種熱管中蒸汽蒸發段與絕熱段的溫差僅相差2 ℃,熱管依然保持良好的傳熱性能。圖6b可看出,無干道平板熱管液體壓降遠大于干道式熱管液體壓降。吸液芯提供的毛細壓頭有限,氣液循環壓降超過最大毛細壓頭時,液體回流量不足,蒸發段吸液芯干涸過熱,導致熱管管壁燒毀。在實際應用中必須避免發生此現象。根據Laplace-Young公式,本文使用的金屬絲網吸液芯能提供的最大毛細壓力為6 443.27 Pa。無干道平板熱管理論上需克服2.94×105Pa的液體壓降才能正常工作,工程上無法實現;而干道式熱管的液體壓降僅為178.66 Pa,足以維持穩定的工質循環和持續傳熱。本文設計的干道式復合吸液芯結構有效提高了平板熱管運行的可靠性。

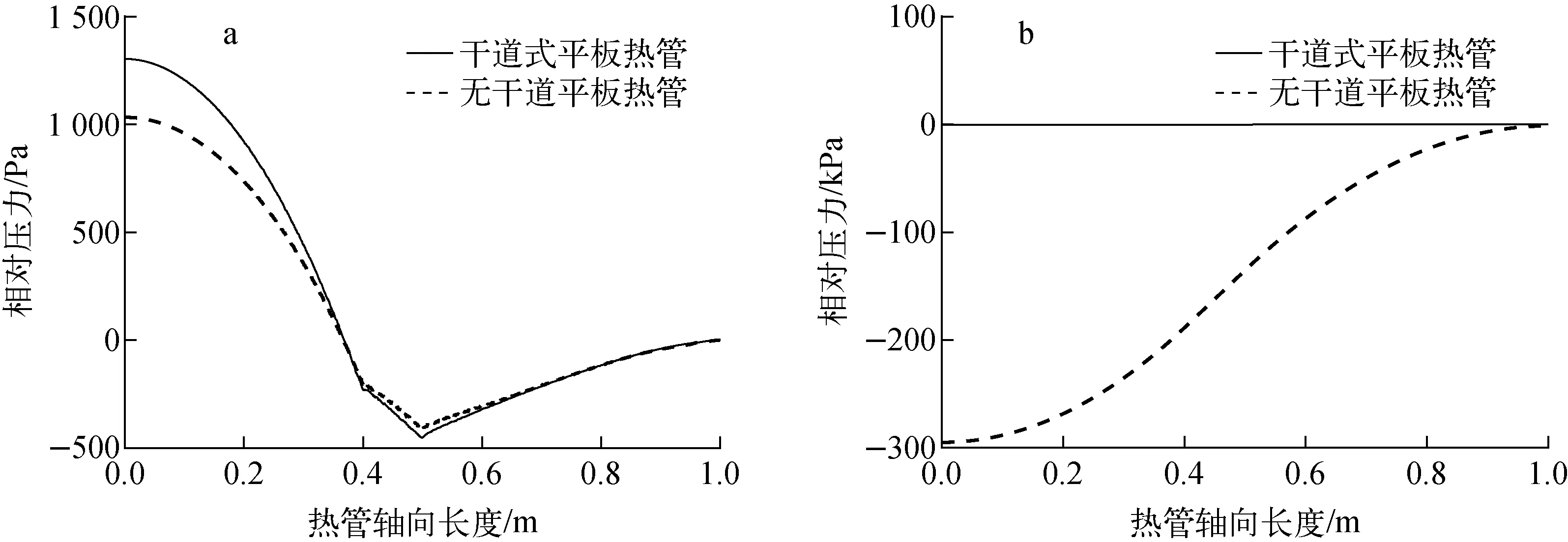
a——蒸汽腔內氣相工質;b——吸液芯內液相工質

圖7示出了干道式平板熱管吸液芯和干道內液相的流速。吸液芯內最大流速為5×10-4m/s,遠小于干道內最大流速0.24 m/s,說明液體主要在干道內流動。液體在吸液芯和干道內的速度分布及流線如圖8所示,可看出液體在冷凝段吸液芯表面冷凝,沿吸液芯周向匯集到干道并沿干道軸向回流至蒸發段,周向充滿吸液芯并在其表面蒸發;與普通熱管液體僅通過絲網吸液芯的回流路徑不同。液體在干道內流動阻力較小且在絲網內周向流動行程很短,解釋了干道式熱管液體壓降遠低于普通平板熱管的原因。

圖7 液相工質在吸液芯和干道中的流速

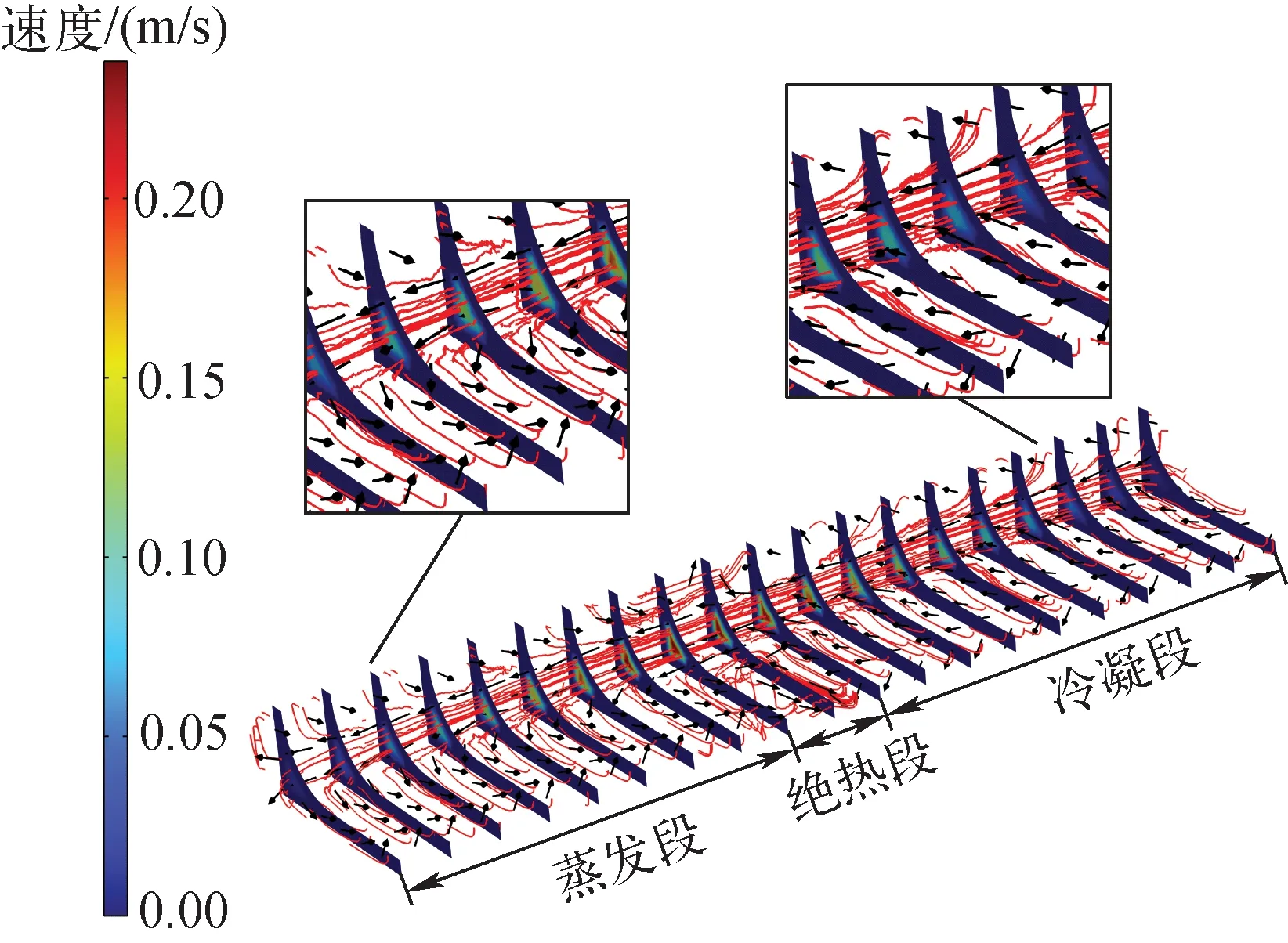
圖8 液相工質在吸液芯和干道中的速度分布及流線

3.2 加熱不均勻度對平板熱管性能的影響

圖9示出了總加熱功率為4 000 W、加熱不均勻度為0和100%時,干道式平板熱管的溫度分布。由圖9可看出,非均勻加熱主要對蒸發段壁面溫度影響較大,其余部分溫度基本不受影響。如圖10所示,當Uf=0%時,蒸發段兩側壁溫對稱分布;隨著加熱不均勻度的增大,蒸發段兩側壁面溫差隨之增大;Uf=100%時,蒸發段兩側壁面溫差達到25 ℃。不同加熱條件下蒸發段靠近側棱處的溫度均更高,與圓熱管管壁周向均溫略有不同。這是由于該處內部為干道,僅靠液體導熱,傳熱較差。圖11示出了Uf=0%～100%時,蒸汽中心軸向溫度、壓力和速度及相對偏差,以Uf=0%時的參數為參考點。蒸汽溫度、壓力和速度最大相對偏差分別為0.6‰、17.5‰、38‰,均小于5%,說明加熱不均勻度對熱管內蒸汽流動傳熱行為特性影響很小。這也是絕熱段、冷凝段壁面能夠保持良好均溫性的原因。

a——單面加熱;b——雙面加熱

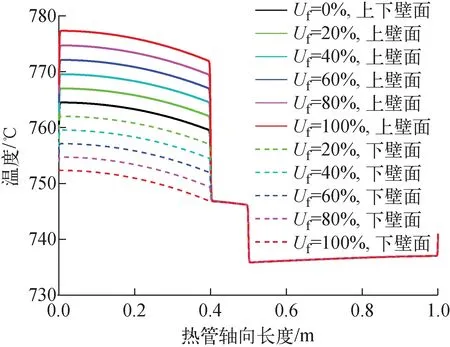
圖10 軸向壁面溫度分布(中心線)

a——蒸汽熱工參數;b——相對偏差

圖12示出了加熱不均勻度為0%和100%時熱管兩側吸液芯內液體壓降,可看出兩種加熱方式下,絕熱段和冷凝段的熱管上下兩側的液體壓降均相同;Uf=0%時蒸發段絕熱(下)側的壓降比受熱(上)側更大,總壓降大于雙面加熱液體總壓降。原因是液體以相同通量回流時,單面加熱造成的總流動阻力更大。但由于干道結構使得總液體壓降較小,可忽略加熱不均勻對液體壓降的影響。

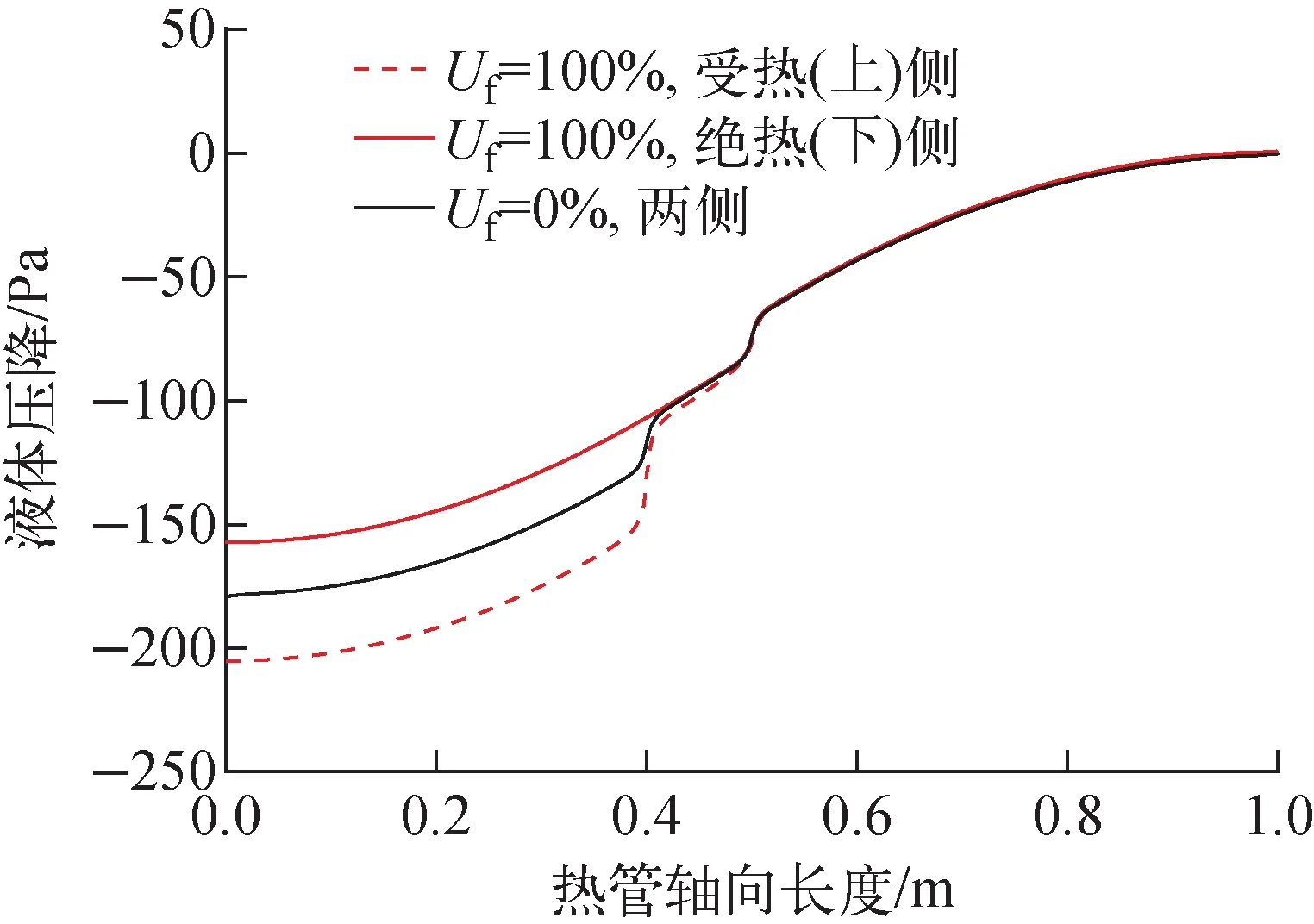
圖12 吸液芯內的液體壓降

熱管通常以溫差、等效導熱系數為穩態評價指標。不同加熱不均勻度下,蒸發段平均溫度均為765 ℃,冷凝段平均溫度均為735 ℃,溫差為30 ℃,等效熱導率為3.02×105W/(m·K)。通過定量分析,可認為加熱不均勻度不影響平板熱管的均溫性和傳熱能力。

非均勻加熱時,平板熱管蒸發段兩側壁面的溫差使熱管殼體在約束下產生熱應力。殼體的最大應力狀態可有效反映熱管的完整性。根據簡單強度理論,當最大應力超過材料屈服強度時,熱管殼體發生塑性變形。熱管在高溫環境下長期工作,高溫蠕變亦會造成殼體的變形及斷裂。圖13示出了加熱不均勻度為50%時平板熱管殼體的等效應力分布。由圖13可看出,在平板熱管蒸發段靠近干道的位置應力較大,原因是此處溫度梯度較大。等效應力峰值在前端蓋熱側頂點處,為93.03 MPa;蒸發段熱流輸入更大的一側應力更大,絕熱段應力最小,冷凝段應力分布較均勻。圖14為加熱不均勻度與最大溫差、最大應力的關系。由圖14可看出,隨著加熱不均勻度的提高,熱管的最大溫差、最大應力也相應增加,且線性關系。當加熱不均勻度達100%時,熱管殼體的最大應力為133.96 MPa,小于該溫度下殼體材料Inconel 718的屈服強度[24](640 MPa),熱管殼體保持結構完整。

圖13 平板熱管應力分布(加熱不均勻度Uf=50%)

圖14 加熱不均勻度與最大溫差、最大應力的關系

反應堆堆芯的徑向功率峰因子的設計限值一般為1.2,即加熱不均勻度為20%。該條件下平板熱管的安全系數較高,約為11.1;考慮殼體的高溫蠕變[25-26],Inconel 718在750 ℃、104h、總變形量1.0%條件下的蠕變極限為70 MPa,蠕變斷裂強度為125 MPa,殼體的最大等效應力小于該限值。平板熱管結構可靠,且等效熱導率高達3×105W/(m·K),可滿足堆芯高效可靠冷卻的要求。

4 結論

本文提出了一種帶有干道的復合吸液芯的平板熱管陣列設計,基于COMSOL建立了其最小特征單元的三維熱流固耦合分析模型,利用該模型對比分析了總加熱功率為4 000 W時,吸液芯結構、加熱不均勻度對平板熱管性能的影響,主要結果及分析如下。

1) 利用方形腔體及雙層吸液芯形成的4個方圓角干道可明顯減低回流阻力,提高傳熱極限,特別在高軸向熱流負荷條件下,必須設置干道;

2) 非均勻加熱不影響熱管內部蒸汽流場,對液體壓降的影響較小,平板熱管依然保持了良好的軸向傳熱性能和均溫性;非均勻加熱使平板熱管殼體熱應力增大,蒸發段受熱面靠近側棱位置的應力較大,最大應力位于前端蓋上頂點,但未超過材料的許用限值;

3) 作為熱板的最小單元,平板熱管對于非均勻高熱流熱邊界條件具有較強的承受能力,軸向傳熱能力強,結構可靠性高,初步證明了熱板具備作為高強度堆芯冷卻傳熱元件的能力。

本文基于COMSOL平臺建立的高溫平板熱管熱流固耦合計算模型具有開放性,能夠快速實現參數化求解,也可用于平板熱管的結構優化及其他異型熱管在特殊熱、力邊界條件下穩態運行性能的評價。