基于軸壓剛度等效的“柱中柱”(CIC)系統等代設計方法研究

房曉俊

(廣州大學 土木工程學院,廣東 廣州 510006)

鋼管混凝土(Concrete Filled Steel Tubular,CFST)因其強度高、延性好、耗能能力強及施工便捷等優點,在高層建筑[1-2]、大跨橋梁[3-4]、海上平臺[5-6]和輸電塔[7-8]等領域得到了廣泛應用。此外,隨著建造技術和新材料的快速發展,高性能混凝土[2,9-10]和高性能鋼材[11-12]也越來越多地被用于CFST構件承載能力的提升和耐久性能的改善。目前,對CFST構件的研究仍然集中于應用新材料和新構造來提升其力學性能。然而鋼管混凝土柱作為高層組合結構中重要的豎向承載力構件存在功能單一的不足,在強烈地震作用下面臨被破壞的風險,可能對結構安全造成嚴重的不利影響,甚至導致結構的倒塌。

近年來,城市抗震韌性研究成為國際防震減災領域的前沿[13-15],為實現城市的震后可恢復,美國、日本和中國等相繼部署了韌性城鄉建設規劃[16-17]。高層建筑作為城市建筑的重要組成部分,保證其足夠的抗震韌性,是建設韌性城市的重要支撐之一。而被動控制技術是在結構局部安裝離散耗散件,根據結構類型和特點選擇合理的控制方案,控制元件易修復、易更換,是提升結構韌性的有效手段[15]。鑒于此,筆者基于被動控制的概念,提出應用于高層結構巨柱的新型組合柱系統,即“柱中柱”(Column-in-Column,CIC)系統[18-19]。CIC系統的提出旨在克服結構柱作為豎向承載構件功能單一的不足,使其兼具結構減振(震)控制的作用,以期解決以彎曲變形為主的高層結構阻尼比增加困難的問題。CIC系統通過增加結構的質量比,為高層結構的振動控制提供了一種有效的實施途徑,從而增強高層結構的抗震韌性,助力韌性城市的建設與發展。本文主要介紹CIC系統的組成和控制機理,基于鋼管混凝土統一理論,采用疊加原理推導CIC系統的截面軸壓組合剛度和軸壓極限承載力的理論公式,最終建立該系統基于軸壓剛度等效的等代設計方法。

1 “柱中柱”系統

具有承載-減振(震)雙功能CIC系統的結構示意圖見圖1。該系統針對廣泛應用于高層結構中的鋼管混凝土柱,取其部分質量當作CIC系統的CFST內柱,剩余部分作為中空夾層鋼管混凝土(Concrete Filled Double Skin Tubular,CFDST)外柱,內柱和外柱通過滑動裝置與柱端連接板形成一體,內、外柱之間預留有空間,用于沿CIC系統高度方向均勻布置一系列的彈簧和消能器。由于常用的柱截面形式有圓形、方形和矩形,組成CIC系統的內、外柱可采用不同的截面形式,因此,可以組合出多種截面形式的CIC系統。圖1(b)列出CIC系統的典型截面形式,主要包括雙圓型、內圓外方型、內方外圓型和雙方型。

圖1 CIC系統的結構示意圖和典型截面形式

CIC系統的振(震)動控制策略為在靜荷載(恒載和活載)作用下,該系統具備與傳統結構柱等同的豎向承載能力,即組成CIC系統的內柱和外柱共同承受豎向荷載。而在橫向動荷載(風、地震等)作用下,CIC系統中的內柱與彈簧和消能器共同組成調諧質量阻尼器(Tuned Mass Damper,TMD)系統,通過調諧子結構(內柱)的動力特性,實現結構“調頻諧振”的作用。與傳統的TMD系統相比,CIC系統具有以下4個特點:

(1)承載力相當。將原結構柱一分為二形成CIC系統,內柱與外柱共同提供與原結構柱等同的豎向承載能力。由于外柱因截面的減小會導致抗剪能力和抗彎能力有所下降,但可通過適當的設計調整(如材料強度、配筋率等)得以彌補。

(2)不需要附加額外的質量。以結構自身的部分質量作為振動響應控制的“附加質量”,可避免或減少傳統TMD-結構系統由于額外質量的附加對結構設計和建筑使用功能產生的影響。

(3)大質量比。內柱自身作為TMD系統中的質量塊,可為結構提供非常可觀的質量比。前期研究表明[19-20],CIC系統的質量比可超過25%,遠大于傳統TMD-結構系統的質量比(通常小于5%[21-22])。

(4)寬頻帶控制。子結構本身具有多個振型,因此,可以拓寬結構振動響應控制的頻帶,且對系統的優化參數不敏感,表現出良好的魯棒性能。

2 剛度和承載力計算

本節基于鋼管混凝土統一理論[23],采用疊加原理推導建立CIC系統的截面軸壓組合剛度和軸壓極限承載力的理論計算公式。考慮到CIC系統內部的連接彈簧和消能器主要用于結構動力響應的控制,因此,在推導其剛度和承載力時,忽略彈簧剛度和消能器阻尼效應的影響,但是軸壓作用下構件的偏心率和長細比等因素對CIC系統靜力性能的影響不可忽略。由于篇幅所限,本節簡要介紹CIC系統的截面軸壓組合剛度((EA)CIC)和軸壓極限承載力(NCIC)的計算公式,詳細的推導見文獻[18]和文獻[24]。

2.1 軸壓組合剛度

根據疊加原理,CIC系統的截面軸壓組合剛度(EA)CIC可將外柱和內柱的截面軸壓剛度相加得到,按式(1)計算:

(EA)CIC=(EA)o+(EA)i,

(1)

式中,(EA)o和(EA)i分別為外柱和內柱的截面軸壓剛度,分別根據《中空夾層鋼管混凝土結構技術規程(T/CCES 7-2020)》[25]和《鋼管混凝土結構技術規范(GB 50936-2014)》[26]計算。

2.2 軸壓極限承載力

類似地,CIC系統的極限軸壓承載力NCIC可按照外柱和內柱分別考慮承載力折減后的極限值疊加得到,如式(2):

NCIC=φoNo+φiNi,

(2)

式中,No和φo為外柱的極限軸壓承載力及其考慮偏心率和長細比影響的承載力折減系數,根據T/CCES 7-2020[25]計算;Ni和φi為內柱的極限軸壓承載力及其承載力折減系數,根據GB 50936-2014[26]計算。

3 等代設計方法

3.1 等代準則

以CFST柱為例,根據其實際尺寸和材料參數,將其等代設計成為軸壓剛度等效的CIC系統(圖2),使得等代前后結構的整體尺寸和承載能力相當,從而便于實現對結構振動響應的控制。圖2所示的幾何參數分別表示對應的鋼管直徑(D,Doso,Dosi,Dis)、厚度(t,toso,tosi,tis)和面積(As,Aoso,Aosi),后續推導不再贅述。

圖2 CFST與CIC等代圖示

為實現等代設計,首先給出如下基本準則:

準則1 等代前后不改變原結構的整體外觀尺寸,即CFST的直徑(D)與CIC系統外柱外鋼管的直徑(Doso)相等,滿足式(3):

D=Doso。

(3)

準則2 為不過多改變原結構的設計,除了保證等代后的CIC系統具有等同的截面受壓剛度外,仍需確保CIC外柱的軸心抗拉承載力與原柱基本相當。鋼管混凝土構件中,混凝土作為受壓材料,抗拉承載力僅考慮鋼材的貢獻[23,27],因此,在使用相同鋼管材料的條件下,僅需滿足鋼管的截面面積相等,即滿足式(4):

As=Aoso+Aosi,

(4)

式中,As,Aoso和Aosi分別為CFST和CIC系統相應鋼管的截面面積。

準則3 實際工程中,CFDST外柱的內、外鋼管厚度往往相等,因此,CIC系統外柱的內、外鋼管厚度亦相等,即滿足式(5):

toso=tosi。

(5)

準則4由第1節可知,CIC系統以結構自身的部分質量作為振動響應控制的“附加質量”,不需要附加額外的質量,需要保證等代前后的總質量相等,即滿足式(6):

mCFST=mCIC,o+mCIC,i,

(6)

式中,mCFST為CFST柱的總質量,mCIC,o和mCIC,i分別為CIC系統外柱和內柱的質量。

3.2 等代設計

3.2.1toso、Dosi和tosi的計算

根據準則2,由圖2所示的幾何尺寸參數,式(4)可進一步改寫為式(7):

πt(D-t)=πtoso(Doso-toso)+πtosi(Dosi-tosi)。

(7)

根據準則1和準則3,將式(3)和式(5)代入式(7),消去Doso和tosi,化簡得到式(8):

t(D-t)=toso(D+Dosi-2toso)。

(8)

對于CFST柱,其總質量mCFST可按式(9)計算:

(9)

式中,h、ρs和ρc分別為柱高(等代前后柱高不變)、鋼管密度和混凝土密度。

假設CIC系統內柱與外柱質量比μ為已知,則由式(6)可得式(10):

(10)

此外,CIC系統的外柱質量mCIC,o還可根據構件的尺寸和材料按式(11)計算:

(11)

將式(3)和式(7)代入式(11),可化簡得到式(12):

2toso)(D+Dosi-2toso)。

(12)

將式(12)代入式(10)可進一步化簡得到式(13):

(13)

顯然,式(13)中mCFST可由式(9)確定,因此,可通過聯立式(8)和式(13),求解一元二次方程組順利得到未知參數toso和Dosi,進而求得tosi=toso。

3.2.2tis和Dis的計算

CIC系統內柱的質量可由式(14)或式(15)計算:

(14)

(15)

令tis=φtoso,其中,φ為內柱鋼管壁厚調整系數,可根據實際的設計需要調整φ的大小,以滿足tis的取值需求。

由式(14)和式(15),令兩式相等化簡得到式(16):

(16)

顯然,式(16)為關于Dis的一元二次方程,其正值解為

(17)

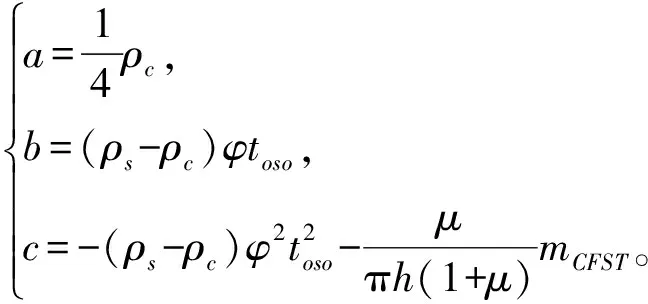
(18)

經過上述求解,便可確定圖2(b)所示的CIC系統各參數的取值。類似地,對于中空夾層鋼管混凝土柱(CFDST)的等代設計,僅需將上述公式中涉及的與CFST相關的計算參數替換成相對應的CFDST的計算參數即可,此處不再贅述。CIC系統的等代設計流程如圖3所示,具體可歸納如下:

圖3 CIC系統等代設計流程

第一步:根據原結構的尺寸確定CIC系統的外柱外直徑Doso。

第二步:根據結構設計的實際需求,給定CIC系統內柱與外柱的質量比μ,由式(8)和式(13),代入原CFST柱的尺寸和材料參數,求得CIC系統外柱外鋼管的厚度toso、外柱內鋼管的直徑Dosi和厚度tosi;

第三步:選取合適的內柱鋼管壁厚調整系數φ計算內柱鋼管的厚度tis,最后根據式(17)和式(18)確定內柱鋼管的直徑Dis,并判斷CIC系統各尺寸參數是否滿足規范T/CCES 7-2020[25]和GB 50936-2014[26]的基本要求;

第四步:根據式(1)計算CIC系統的截面軸壓組合剛度是否與原CFST柱等效,若滿足,則完成等代設計,否則重復第二步至第四步,直至等代完成。

4 算例分析

為檢驗本文提出的基于截面軸壓剛度等效的CIC系統等代設計方法,本節分別選取Huang等[28]試驗中的CFST試件和Tao等[29]試驗中的CFDST試件為例,參照圖3所示的等代設計流程,對這兩種類型(實心和空心)的試件采用第3節的等代設計方法進行設計,以檢驗所提方法的準確性和可靠性。試件的基本尺寸和材料信息見表1。為方便計算,等代設計過程中鋼材和混凝土的密度分別取為ρs=7 800 kg/m3和ρc=2 400 kg/m3。根據表1中試件的信息,取質量比μ=0.55,內柱鋼管厚度調整系數φ=1,經過等代設計,計算得到的CIC系統尺寸參數如表2所示。表2中,構件編號的數字表示CIC系統外柱外鋼管的徑厚比。

表1 CFST和CFDST試件尺寸和材料信息

表2 CIC系統尺寸表

圖4 等代設計結果對比

由圖4可知,計算得到的CIC系統的截面軸壓剛度與原CFST或CFDST試件相比誤差最大值為9.68%,均值為6.31%,相應的質量誤差非常小(<1.5%),具有良好的等代效果,檢驗了所提出等代設計方法的準確性和可靠性。同時,采用本文提出的基于截面軸壓剛度等效的CIC系統等代設計方法,計算得到的軸壓極限承載力之間的偏差小于3%,表明經過等代設計得到的CIC系統具有與原結構基本等同的豎向承載能力,進一步說明基于疊加原理建立的CIC系統的理論計算公式在實現軸壓剛度等效的同時可保證結構具有可靠的承載能力。

5 結 論

本文提出一種具有“承載-減振(震)”雙功能的“柱中柱”(CIC)系統以增強高層組合結構的抗震性能。采用鋼管混凝土“統一理論”的疊加原理推導CIC系統的截面軸壓組合剛度和軸壓極限承載能力的計算公式,在此基礎之上建立基于截面軸壓剛度等效的CIC系統等代設計方法并檢驗了該方法的準確性。主要得到以下結論:

(1)根據鋼管混凝土“統一理論”,采用“疊加”原理,便于建立CIC系統的截面軸壓組合剛度和軸壓極限承載力的理論計算公式。

(2)經等代設計,CIC系統與原結構柱具有基本相當的截面軸壓剛度,且兩者之間的質量和軸壓極限承載力基本等同。其中,等代前后截面軸壓剛度誤差小于10%,質量和軸壓極限承載力誤差均小于3%,表明提出的等代設計方法具有良好的準確性和可靠性。

(3)提出的基于軸壓剛度等效的CIC系統等代設計方法可同時適用于CFST和CFDST結構柱的等代設計,該方法簡明直接,契合我國現行規范要求,可為今后的工程設計與分析提供參考。