“非指示性”教學模式下初中數學課堂教學初探

王曉欣

一、探究背景

“非指示性”教學由浙江師范大學鄭逸農教授于2000年提出，是對以教師為中心的”指示性“教學的一種反撥，其更重視的是學生的自主探究、自主成長和學生在學習中的主體地位。其核心思想和準則與《義務教育數學課程標準（2022版）》的精神是吻合的。

《義務教育數學課程標準（2022版）》中指出義務教育階段的數學培養目標是使得人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展，逐步形成適應終身發展需要的核心素養。而在“非指示性”教學中也要求在布置任務時，教師應該依據學生自身的發展水平將要求設置為三個維度，難度由低到高，讓每個學生都參與，也讓不同層級的學生達到不同層級的要求，甚至可以做得更好，體現了維果茨基的“最近發展區”的教學理念。

“非指示性”教學還要求在課堂教學中應該遵循“先生后師”的原則，這與課程標準中“學生是學習的主體，教師是學習的組織者、引導者與合作者”也是相吻合的。

如何在數學課堂中貫徹落實課程標準中的精神是一線教師一直關注并實踐的重點。所以筆者以浙教版七年級上冊《5.1一元一次方程》為例，進行了“非指示性”教學模式下初中數學課堂教學初探，訴諸筆端，與諸君共享。

二、探究過程

（一）情境創設，引入新知

1.游戲：猜年齡

問題1：猜一猜老師的年齡是多少歲？

（設計意圖：調動課堂氛圍，引導學生進入上課狀態。）

問題2：老師的年齡乘以2再加上4剛好是60，老師多少歲？你是如何計算出老師的年齡的？

（設計意圖：引導學生回顧小學學過的算式法和方程法。）

問題3：同學們，你們還記得什么叫做方程嗎？

（設計意圖：回顧方程的概念，為一元一次方程概念的引出作鋪墊。）

2.陽光體育大課間

任務：列出下列三個問題中的方程。

（1）一個排球按照原價8折銷售的售價為32元，這個排球的原價是多少元？

設這個排球的原價為x元，可列出方程________.

（2）小華和小全兩人共跳繩330下，小華比小全多跳30下，小全跳了多少下？

設小全跳了x下，可列出方程_______________.

（3）小強、小紅，小杰和張明四位同學進行投籃比賽，每人投了10次，小強投進6個，小紅比張明多投進2個，小杰比張明少投進2個，四個人平均每人投進的個數為6個，問張明投進多少個？

設張明投進x個，可列出方程________________.

要求：正確、快速、簡潔。

時間：3分鐘。

問題1：有沒有同學愿意與同學們分享你的三個方程及列方程的思路？

問題2：觀察上述三個方程，它們有什么共同點？

（設計意圖：結合學生的生活實際并根據“非指示”性教學模式設置學習任務，一是引出一元一次方程的概念，二是貫徹落實學生的學習主體地位。）

3.數學史的學習

問題1：同學們，你們知道一元一次方程中元的含義是什么嗎？為什么我們將未知數稱之為元？讓我們一起了解“元”的由來吧！

數學史材料：

著名的中國古代數學著作《九章算術》中有專門一章研究方程，但古代數學家表示“方程”時，沒有使用專門的記法來表示未知數。

宋元時期，中國的數學家們創立了“天元術”，用天元來表示未知數x，“立天元一”相當于“設未知數x”。

（二）概念辨析，理解新知

任務：判斷下列各式是不是一元一次方程，如果不是，請說明理由。

（1）3x+4? ? （2）-5x=7? ?（3）√x+1=5

（4）3x-2y=1 （5）x=6? （6）1-x2=0

要求：正確、快速、簡潔。

時間：2分鐘。

問題1：請同學們四人小組內分享自己的答案，比較是否有所不同，如果有，請組內統一答案。

問題2：以四人小組為單位，選派一名小組代表上臺分享小組的成果。

問題3：通過該問題的解決，你能說一說判斷一個方程是否是一元一次方程的關鍵什么嗎？

（三）深入探究，再探新知

1.概念引出：一個排球按照原價8折銷售的售價為32元，這個排球的原價是多少元？

剛剛已經列出方程：設這個排球的原價為x元，

0.8x=32

問題1：你能算出這個排球的原價嗎？請說說你是如何計算的。

問題2：你的答案正確嗎？你是如何驗證的？

概念：像x=40這樣能使一元一次方程左右兩邊的值相等的未知數的值叫做一元一次方程的解，也叫做方程的根。

設計意圖：讓學生直觀感受一元一次方程的解的概念。

2.概念鞏固：小華和小全兩人共跳繩330下，小華比小全多跳30下，小全跳了多少下？

設小全跳了x下，列出方程2x+30=330。

例1 判斷下列x的值是不是一元一次方程2x+30=330的解，并說明理由。

（1）x=140? ? ? ? ? ? ? ? ? ? ? ? ? ?（2） x=150

問題1：x=140是不是該方程的解？你是如何判斷的？（教師書寫格式規范）

問題2：請你們仿照老師的格式，重新書寫判斷x= 150是不是該方程的解的過程。

（設計意圖：理解鞏固一元一次方程的解的概念，掌握規范的書寫格式。）

3.概念深入：小強、小紅，小杰和張明四位同學進行投籃比賽，每人投了10次，小強投進6個，小紅比張明多投進2個，小杰比張明少投進2個，四個人平均每人投進的個數為6個，問張明投進多少個？

設張明投進x個，列出方程3x+6/4 = 6

問題1：在剛剛的問題中，是老師給了大家兩個數字，分別是x=140和x=150去判斷它們是否是方程的解。但是現在這個問題中，老師并沒有提供數字，同學們，你們能夠自己去試著找一找該方程的解嗎？

問題2：老師發現部分同學，已經直接對這個方程進行了求解。會對該方程求解的同學請舉手。（部分學生舉手）這部分同學非常不錯，已經超前掌握了我們后面的學習內容。那除了超前使用后面的學習內容之外，我們還有其他方法去找一找這個方程的解嗎？（有學生回答：猜。）

問題3：那我們如何猜呢？根據什么去猜呢？請四人小組合作有理有據地猜一猜吧。

生1：小紅最多投進10個，張明比她少兩個，所以張明最多投進8個。小杰最少投進0個，張明比她多兩個，所以張明最少投進2個。所以x應該在2和8之間。

生2：x還應該是整數，投球沒有半個。

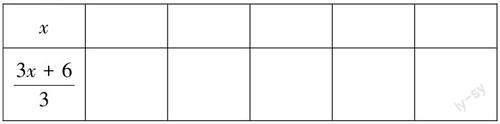
問題4：請同學利用下列表格去試著找一找該方程的解。

問題5：該方程的解是多少？

生：x=6

問題6：該方程還有其他解嗎？請同學們結合表格回答這個問題.

生：沒有了，因為隨著x的增大，（3x+6）/3的值也隨之增大，隨著x的減小，（3x+6）/3的值也隨之減小。

總結：像剛剛這樣子尋找該方程的解的方法叫嘗試檢驗法，是我們數學中解決問題的一種重要方法。

（設計意圖：讓學生積累處理未知問題的數學經驗，提升學生的數學思維。）

（四）總結歸納，回顧新知

通過本節課的學習，同學們，你有什么收獲？

三、探后思考

（一）先生后師，尊重學生

“非指示性”教學要求在課堂教學過程中，教師通過問題和環節的合理設置，先由學生自主思考，自主解決，而后再由教師評價指導，體現學生學習主體的地位，尊重學生的差異。

在本次探究中，筆者基本已經按照“先生后師”的原則進行課堂教學，從而達到了以下兩個尊重，體現學生的學習主體地位。

1.尊重學生的差異

學生認知發展水平的差異是客觀存在的，在課堂上如何處理學生的認知差異是對教師的考驗。在本次教學探究過程中，筆者牢牢抓住了“非指示性”教學的三級要求，在尊重學生的差異的基礎上，力求讓不同學生達到不同的要求，不同的學生得到不同的發展。如在概念辨析過程中，對學生的三級要求是：正確、快速、簡潔。正確是最低層級的要求，是預設班里大部分學生要達到的水平，是對一元一次方程的概念達到一個了解的狀態。快速是在正確基礎上的進一步要求，不僅僅要求學生的正確率，也要求學生的速度。簡潔是最高層級的要求，也是對學生新知識學習水平的考查。若學生能夠在前兩級要求的基礎上簡潔表述出理由，這就說明了學生對于一元一次方程這一概念由了解進入到了理解這一狀態。

2.尊重學生的心理發展

初中生正處于青春期階段，此時的他們對于外界充滿了好奇心，也樂于幫助他人。在概念辨析過程中，筆者先由學生自主完成對6個式子的判斷并思考理由。結束后，筆者并不著急公布答案。而是選擇了讓學生之間互相交流。這是為何？因為此時的他們最好奇的不僅僅是自己的答案正確與否，更好奇同伴做得如何。通過他們的交流，再讓學生組內合作統一答案，既能讓學生在交流的過程中重新理清一元一次方程的概念，糾正認知偏差，也能讓學生互相幫助，體會幫助他人和學習數學的樂趣。

“非指示性”教學模式中的“先生后師”，尊重了學生，確確實實地讓學生成為了學習的主體，而老師則是作為了組織者、引導者和合作者。

（二）問題驅動，引領思維

“非指示性”教學在數學課堂實踐中要以問題驅動為導向組織教學活動，通過問題來引領思維。本節課的教學難點是嘗試檢驗法的引出和理解。為什么要用嘗試檢驗法去找方程解是很多學生難以理解的，也是在日常教學中很多老師會一筆帶過的。如果一筆帶過，那顯然是錯過了培養學生數學思維的一個好機會。嘗試檢驗法是引導學生思考在未知情況下該如何解決數學問題，從何處突破的重要方法。

在本次教學活動過程中，筆者利用陽光體育大課間這一活動中列出的三個一元一次方程層層推進：1.通過求排球的原價和如何判斷x=40是否正確這兩個問題先引出一元一次方程的解的概念，讓學生直觀感知；2.在跳繩問題中，筆者給出x=140和x=150，讓學生判斷其是否是方程的解。目的在于讓學生理解鞏固一元一次方程的解的概念；3.投籃問題中方程的解是多少？如何去求？這是在前兩個問題基礎上的進一步提升。在跳繩問題中，是由教師給出兩個值進行判斷是否是方程的解，那么投籃問題中教師沒有對x進行賦值，又該如何解決呢？

通過上述層層推進，對于投籃問題中方程的解，此時的學生分為了三類：一是直接求解型；二是猜測驗算型；三是茫然無知型。筆者肯定直接求解型的同學，學在前列，而后側重引導學生猜測驗算，引導學生思考是否可以確定x的大致范圍及其方法和依據。

通過上述三個問題的遞進，不僅引導學生理解掌握了一元一次方程的解的概念，也讓學生積累了處理未知問題時的數學經驗，是對學生數學思維的一種提升。

“非指示性”教學模式是符合新課程標準的精神的，是值得我們繼續嘗試和挖掘的。路漫漫其修遠兮，吾將上下而求索。