YTSF方程的Lie點對稱群及其非行波動力學行為

陳 煒, 鮮大權, 蒲志強

(1. 西南科技大學 數理學院, 四川 綿陽 621010; 2. 綿陽師范學院 數理學院, 四川 綿陽 621010)

0 引言

非線性演化方程(NLEEs)精確解的研究在非線性科學領域具有重要科學意義[1].由它們推導出的孤波[2]、怪波[3]、Lump波[4]、Lump-Stripe混合波[5]等科學地解釋了相關物理現象.對非線性演化方程精確解的研究發展了很多重要的非線性數學物理方法,如反散射法、Lie群法、B?cklund變換法、Hirota雙線性法[6-8]、Bell多項式法[9]、CRE法、變量分離法、CKdV法等[10-11].

本文考慮如下形式的(3+1)維Yu-Toda-Sasa-Fukuyama(簡稱YTSF)方程

(-4ut+φ(u)uz)x+3uyy=0,

(1)

其中,u=u(t,x,y,z)是尺度空間坐標x、y、z和時間坐標t的解析函數.YTSF方程是由Ablowitz和Musslimani構造的Bogoyavlenshii-Schiff方程的推廣形式[12],該方程描述了兩層液體的界面波[13].YTSF方程已經有很多研究,已有的研究發現該方程顯示了縱橫方向的兩類色散性[14],有豐富的強脈沖動力學行為[15],存在類孤子解[16]、Lump解[17-18]、有理同宿解[19]、一般高階怪波解[20]和周期孤子解[21]、交叉孤波[22]和雙周期波解[23]、非行波解[24]、多波解[25]、孤子類解[26]、指數函數解、雙曲函數解[27]、三角函數解[28]、周期類孤波解[29]、Lump波解[30]、非行波精確解[31-32]等.

本文將應用Lie群方法尋求方程的Lie點對稱,針對對稱約化方程的不同特點,分別采用Jacobi橢圓函數展開法、CRE展開法和分離變量法求解對稱約化方程,進一步應用計算機數字圖像技術分析所得原方程的非行波動力學行為的局域激發模式.

1 方程的Lie點對稱

首先,將變換u=vx代入方程(1)并對x積分一次,取積分常數為零,則得YTSF方程(1)的勢形式(pYTSF)如下:

vxxxz+4vxvxz+2vxxvz+3vyy-4vxt=0.

(2)

設方程(2)的Lie點對稱為σ=σ(t,x,y,z,v,vt,vx,vy,vz,…),依據Lie群理論,σ滿足以下方程

σx3z+4σxvxz+4σxzvx+2σxxvz+σzvxx+

σyy-4σxt=0.

(3)

設

σ=f1vx+f2vy+f3vz+f4vt+f5v+f6,

(4)

其中,fi(i=1,2,…,6)為變量t、x、y、z的待定光滑函數,v=v(t,x,y,z)滿足方程(2).將(4)式連同方程(2)代入方程(3),則有

f1zvx4+f2zvx3y+f4zvx3t-(3f1xz+f5z)vx3+

3f4xvx2zt+3f2xvx2yz+3f3xvx2z2+…=0.

(5)

基于函數v對t、x、y、z的各階導數的線性無關性可獲得

f3=p3(t),f4=λ,f5=0,

(6)

將(6)式代入(4)式,則得方程(2)的Lie點對稱如下:

p2(t)vy+p3(t)vz+λvt+

(7)

其中,pi(t)(i=1,2,3,4,5)是時間變量t的任意光滑函數.

2 方程(2)的Lie點對稱約化

由于(7)式中含有5個t的任意函數,該對稱的內涵很豐富,由它可得到方程(2)的一系列對稱約化方程.基于約化方程的可積性,本文考慮其中的如下3種情況.

1) 取

λ=1,p1(t)=p2(t)=p4(t)=p5(t)=0,

p3(t)=p′(t).

(8)

將(8)式代入(7)式,則有

σ=p′(t)vz+v

(9)

求解方程σ=0,得方程(2)的一個Lie點對稱變換如下:

ξ=z-p(t),

(10)

其中f(x,y,ξ)為待定函數.將變換(10)代入方程(2),則方程(2)約化為如下的關于函數f(x,y,ξ)的2+1維常系數非線性偏微分方程:

2fxxfξ+4fξxfx+3fyy+fξxxx=0.

(11)

2) 取

λ=1,p1(t)=0,

p2(t)=0,p3(t)=0.

(12)

將(12)式代入(7)式得

σ=v

(13)

方程σ=0的解是

v=-yp4(t)-p5(t)+f(x,y,z).

(14)

將(14)式代入方程(2),則方程約化為如下的關于函數f(x,y,z)的2+1維常系數非線性偏微分方程:

fxxxx+4fxfxz+2fxxfz+3fyy=0.

(15)

3) 取

λ=1,p1(t)=p(t),p2(t)=3t,

p3(t)=p4(t)=p5(t)=0.

(16)

將(16)式代入(7)式有

σ=2vxy+vxp′(t)+3tvy+vt+2zp″(t).

(17)

方程σ=0有解:

v=-2zp′(t)+

(18)

12fξfξz+6fξξfz-36ηfξξ+3fξξξz+4fηη=0.

(19)

以上應用方程(2)的Lie對稱(7)式的3種情況(8)、(12)和(16)式,分別將方程(2)對稱約化成了低一維的非線性偏微分方程(11)、(15)和(19)式.針對這3個約化方程的不同特點,下面分別采用Jacobi橢圓函數展開法、CRE展開法和分離變量法求解這3個對稱約化方程.

3 對稱約化方程求解

3.1 Jacobi橢圓函數展開法求解方程(11)取波變換

f=p(η),η=αx+βy+γξ,

(20)

其中α、β、γ為待定非零波參數,將(20)式代入方程(11),得函數p(η)滿足的四階非線性常微分方程如下:

6α2γp″(η)p′(η)+α3γp(4)(η)+

3β2p″(η)=0.

(21)

方程(21)對η積分一次,取積分常數為B有

3α2γp′(η)2+α3γp(3)(η)+

3β2p′(η)+B=0.

(22)

3α2γq(η)2+α3γq″(η)+

3β2q(η)+B=0.

(23)

α3γq′(η)2+2α2γq3(η)+3β2q2(η)+

2Bq(η)+2C=0.

(24)

3.1.1Jacobi橢圓正弦函數展開 設

q(η)=a1sn2(bη,m)+a0,

(25)

其中sn為Jacobi橢圓正弦函數,模m∈(0,1),a0、a1、b為待定常數,a1b≠0.將(25)式代入方程(24),取sn的各次冪項系數為零,得待定常數滿足的非線性代數方程組如下:

當取積分常數為

時,方程組(26)有解:

a1=-2αb2m2.

(27)

將(27)式代入(25)式有

q1(η)=-2αb2m2sn2(bη,m)+

(28)

當m→1時,(28)式化為沖擊波解

q2(η)=-2αb2tanh2(bη)+

(29)

令(29)式中b=bi,i2=-1,則(29)式化為周期波解

3.1.2Jacobi橢圓余弦函數展開 設

q(η)=a1cn2(bη,m)+a0,

(31)

其中cn為Jacobi橢圓余弦函數,模m∈(0,1),a0、a1、b為待定常數,a1b≠0.將(31)式代入方程(24),取cn的各次冪項系數為零,則待定常數滿足的非線性代數方程組為:

當取積分任意常數為

時,方程組(32)有解:

a1=2αb2m2.

(33)

將(33)式代入(31)式有

q4(η)=2αb2m2cn2(bη,m)-

(34)

當m→1時,(34)式化為孤立波解

令(34)式中b=bi,i2=-1,則得周期波解

將以上所得方程(24)的解qi(η)(i=1,2,…,6)依次代入變換(20),則得約化方程(11)的解依次如下:

f1(x,y,ξ)=-2αb2m2sn2(b(αx+βy+γξ),m)+

(37)

f2(x,y,ξ)=-2αb2tanh2b(αx+βy+γξ)+

(38)

f3(x,y,ξ)=2αb2tan2b(αx+βy+γξ)+

(39)

f4(x,y,ξ)=2αb2m2cn2(b(αx+βy+γξ),m)-

(40)

f5(x,y,ξ)=2αb2sech2b(αx+βy+γξ)-

(41)

f6(x,y,ξ)=-2αbsec2b(αx+βy+γξ)+

(42)

3.2 CRE展開法求解方程(15)作變換

f=p(ξ,y),ξ=rx+sz,

(43)

其中r、s為待定非零波參數.將(43)式代入方程(15),則方程(15)約化為如下1+1維非線性偏微分方程:

r4pξξξξ+6r2spξpξξ+3pyy=0.

(44)

假設

p(ξ,y)=α+βU(τ).

(45)

同時U(τ)滿足如下形式的Riccati方程:

Uτ=μ0+μ1U2,

(46)

其中,α=α(ξ,y),β=β(ξ,y),τ=τ(ξ,y)均為ξ、y的待定光滑函數,μ0和μ1為待定常數,μ1≠0.將(45)式連同方程(46)代入方程(44),則有

2τξβ(3μ1rτξξ+2βξ)+τξξβ2)U4+…=0.(47)

(48)

Riccati方程(46)當μ0μ1<0時有解:

(49)

將(48)和(49)式代入(45)式,得方程(44)的解為

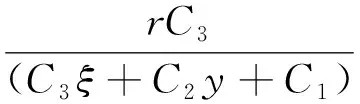
C2y+C1)+C).

(50)

應用變換(43),相應獲得約化方程(15)的解如下:

f(x,y,z)=

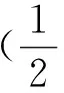
(51)

3.3 變量分離法求解方程(19)設該方程有如下形式的和式變量分離解:

f(z,ξ,η)=p(η,z)+q(ξ),

(52)

其中,p(η,z)是η、z的待定光滑函數,q(ξ)是ξ的待定光滑函數.將(52)式代入方程(19),則有

6qξξpz-36qξξη+4pηη=0.

(53)

方程(53)分離變量有

(54)

(55)

求解方程組(55)可得

(56)式代入(52)式,得方程(19)的和式變量分離解如下:

f(z,ξ,η)=C3(C5eC2η+C6e-C2η)e

其中Ck(k=1,2,…,6)均為積分常數,且

對稱約化方程(11)和(15)還可用雙線性法、變量分離法等不同方法求解,因此可獲得更加豐富的不同解結構.但方程(19)是變系數非線性偏微分方程,它無行波解、行波法與變量分離法以外的其他方法可否求解值得進一步研究.

4 YTSF方程(2)的非行波新解

1) 將(37)～(42)式分別代入變換(10)依次獲得:

βy+γ(z-p(t))),m)+ω1,

(58)

2αb2tanh2b(αx+βy+γ(z-p(t)))+ω2, (59)

βy+γ(z-p(t)))+ω3,

(60)

βy+γ(z-p(t))),m)-ω4,

(61)

βy+γ(z-p(t)))-ω5,

(62)

βy+γ(z-p(t)))+ω6,

(63)

其中

2) 將(51)式代入變換(14)有

v7=-yp4(t)-p5(t)+

C2y+C1)+C).

(64)

3) 將(57)式代入變換(18)有:

(a)C0=C7=0,C5C6=C3=τ=1時,有

2(2t3-2ty-p(t)+x)2+

C1(2t3-2ty-p(t)+x).

(65)

(b)C0=C7=0,C3=τ=1,C5C6=-1時,有

C1(2t3-2ty-p(t)+x)+C0.

(66)

5 方程(2)的動力學行為局域激發模式

本節以(64)式為代表分析方程的動力學行為局域激發模式.

1) 取C=-1,r=1,s=1,C1=1,C2=-3,p4(t)=sin(t),p5(t)=sech(t)和x=X,y=X,z=X,則在(X,t,v)空間的局域激發模式如圖1所示.

(a) C3=0.1 (b) C3=1 (c) (X,t)面的等高線

圖1中,沖擊波與對數波在X方向復合,在時間t方向周期演化,隨參數C3的增大,演化出的周期明孤子向X軸正向的沖擊波波峰方向移動.

(a) C2=3 (b) C2=3.5 (c) (X,t)面的等高線

在圖2(a)中,在X=-4.5左側為明孤子,在X∈[-4,-2]演化為沖擊波,隨參數C2的增大波能量沿X軸正向增加,在X∈[-4.5,-4]演化出奇異波,發生能量聚集現象.C2=3.5時則在X∈[-3.5,-3]時才出現能量聚集現象,如圖2(b)所示.

3) 取C=-1,r=1,s=1,C1=1,C2=-3,p4(t)=sin(t),p5(t)=sech(t)和x+y-z=X在當前(X,t,v)空間的局域激發模式如圖3所示.

(a) C3=0.1 (b) C3=1 (c) (X,t)面的等高線

圖3(a)中,沖擊波與對數波在X軸方向復合演化,在t軸方向周期演化.C3=1時在周期沖擊波的X=0附近演化出周期孤子,如圖3(b)所示.

6 結束語

本文獲得了含有5個關于時間t的任意函數的Lie點群對稱(7),在3種情況下求得了YTSF方程的對稱約化方程(11)、(15)和(19).用Jacobi橢圓函數展開法求解方程(11),獲得了非行波周期解、孤子解等6個.用CRE展開法求解方程(15),獲得相容Riccati方程解1個.用變量分離法求解了變系數方程(19),獲得和式變量分離解2個.應用計算機數字圖像技術分析了函數v8所蘊涵的YTSF方程的動力學局域激發模式.本工作的全新結果表明了YTSF方程可積性及其動力學行為特性的豐富多樣性,實證了多種非線性數學方法有機結合的有效性.

該方程基于對稱(7)的更多對稱約化方程的可積性及相應動力學行為特征有待進一步研究.

致謝西南科技大學校級教改項目(20GJZX14)對本文給予了資助,謹致謝意.