用角的關系,求動點的坐標
甘肅省武威第十中學(733000) 鄭利年 陳國玉
二次函數為載體的與角度有關的這類問題,是近幾年中考的熱點之一,這類題綜合性強,有利于提高同學們的解題能力. 下面將這類問題中的常見題型歸納如下,供同學們學習時參考.
1 用特殊角求動點的坐標
例1如圖1,已知頂點為C(0,-3)的拋物線與x軸交于點A,B,直線y=x+m過頂點C和B.
(1)求函數y=ax2+b的解析式;
(2)拋物線上是否存在點M,使得∠MCB= 15°,若存在,求出點M的坐標;若不存在,請說明理由.
分析: (1)先將C點坐標代入y=x+m中即可求出m的值,再求出直線y=x+m與y軸的交點B的坐標,然后將B,C點坐標代入y=ax2+b中,利用方程組即可求出解析式;(2)分M在點B的上方或下方兩種情況. 利用特殊角,求出直線CM與x軸的交點的坐標,從而求出直線CM的解析式,聯立解析式y=ax2+b,即可求得點M的坐標.
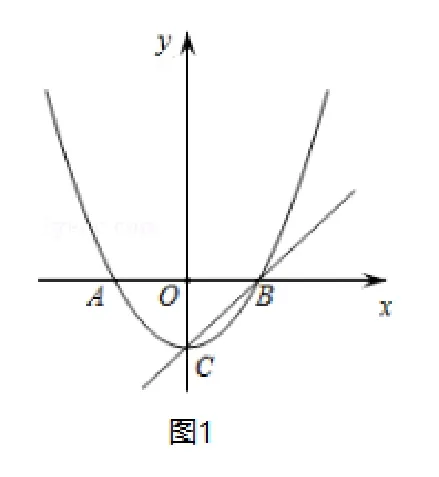
解: (1) 將C(0,-3) 代入y=x+m, 得m= -3; 直線y=x-3 與x軸交于點B, 當y= 0 時可得x= 3,點B的坐標為(3,0),將(3,0),(0,-3)代入y=ax2+b中得∴二次函數的解析式為
(2) 存在, 如圖2, ∵B(3,0),C(0,-3),∴OB=OC,∴∠OCB=45°. 分以下兩種情況:
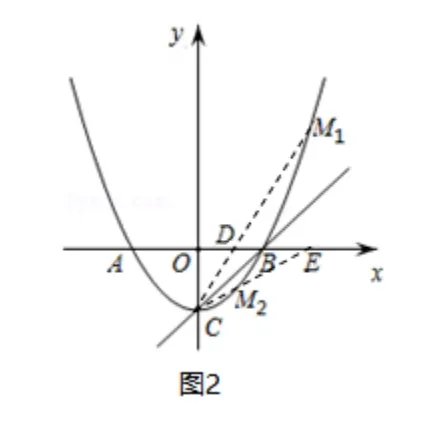

2 用兩角相等,求動點的坐標
例2如圖3, 直線y= -x+3 與x軸、y軸分別交于B、C兩點,拋物線y=-x2+bx+c經過點B、C,與x軸的另一交點為A,頂點為D.
(1)求拋物線的解析式;
(2) 在拋物線的對稱軸上是否存在一點P, 使得∠APB= ∠OCB? 若存在, 求出P點坐標; 若不存在, 請說明理由.
分析: (1) 先利用方程求出點B與點C的坐標, 代入y= -x2+bx+c中即可求得解析式;(2)分P在x軸上方或下方兩種情況討論. 由題意可知ΔBOC是等腰直角三角形,得到∠APB=45°,通過構造直角三角形,利用勾股定理建立方程即可求出點P的坐標.
解:(1)直線y=-x+3 與x軸、y軸分別交于B、C兩點,則點B、C的坐標分別為(3,0),(0,3),將點B、C的坐標代入二次函數y=-x2+bx+c解析式,得解得故函數的解析式為y=-x2+2x+3;
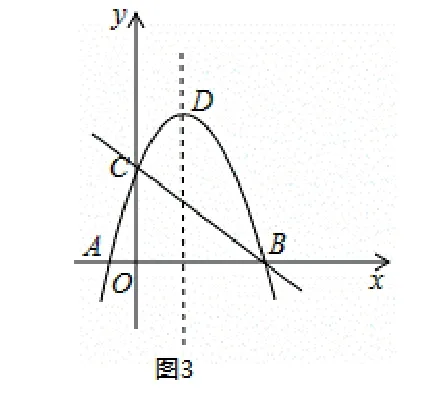
(2)存在. 因為A點與B點(3,0)關于直線x= 1 對稱,所以點A(-1,0)

3 用兩角和的關系,求動點的坐標
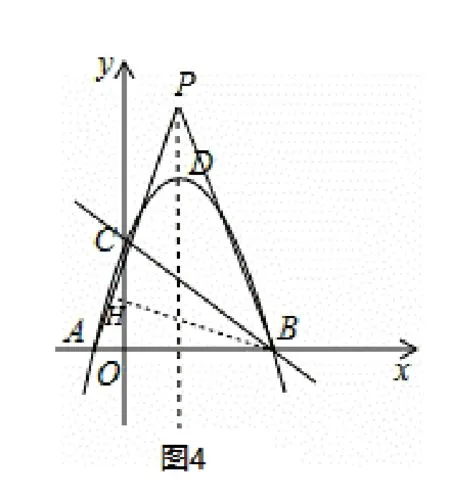
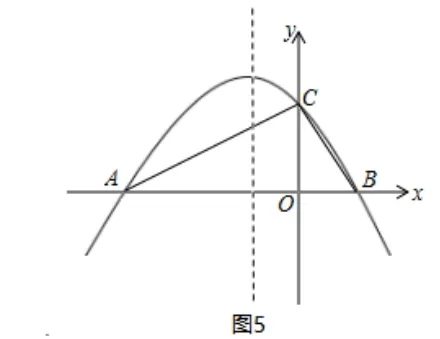
例3如圖5, 已知拋物線y=ax2+bx+c與x軸交于點A,B,與y軸交于點C. 其中A(-6,0),B(2,0),C(0,3),連接AC,BC.
(1)求拋物線的解析式;
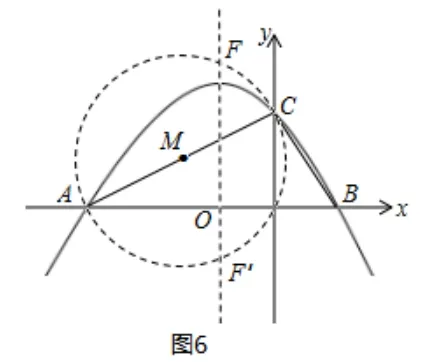
(2)拋物線的對稱軸上是否存在一點F,使得∠FAC+∠FCA= 90°? 若存在,求出點F的坐標;若不存在,請說明理由[2].
分析: (1)利用交點式y=a(x-x1)(x-x2)即可求得解析式;(2)使得∠FAC+∠FCA= 90°,聯想到“直徑所對的圓周角為90°”和“直角三角形中,兩銳角互余.”可以AC為直徑作圓,與對稱軸的交點即為F結合勾股即可求解.
解: (1) 拋物線與x軸交于點A,B, 設其解析式為y=a(x-x1)(x-x2), 將A(-6,0),B(2,0) 代入, 得y=(x+6)(x-2),再將C(0,3)代入,解得所以拋物線的解析式為

4 用兩角倍的關系,求動點的坐標
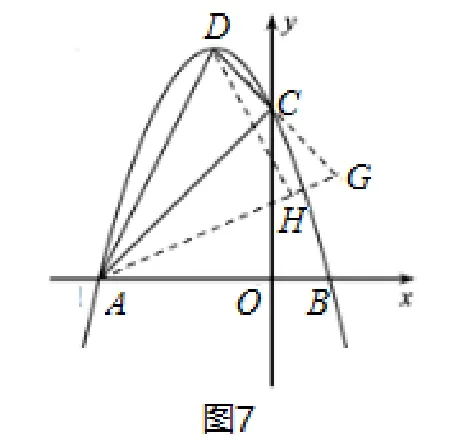
例4已知二次函數y=ax2+bx+6 的圖像開口向下,與x軸交于點A(-6,0)和點B(2,0),與y軸交于點C.
(1)求二次函數的關系式;
(2)如圖7,該函數圖像的頂點為D,在該函數圖像上是否存在點E,使得∠EAB=2∠DAC,若存在請求出點E的坐標;若不存在請說明理由.
分析: (1)將點A和點B的坐標代入拋物線的解析式中,求得a,b的值,即可得到解析式;
(2) 根據勾股逆定理證得∠ACD= 90°, 延長DC至G, 使CG=DC, 連接AG, 過點D作DH⊥AG, 得到∠DAG= 2∠DAC, 利用面積法求出DH的長, 再求得sin ∠DAG= sin ∠EAB,進而得出tan ∠EAB,利用一次函數的性質得到一次函數的解析式,再與拋物線的解析式聯立方程組即可求解.


總之,以二次函數為載體的角度相關問題,通常要構造直角三角形,利用勾股定理建立方程求解;或利用三角函數求出一次函數的解析式,再聯立拋物線的函數式,通過解方程組求解;或通過特殊角構造直角三角形進行求解.

