斜風下斜拉-懸吊組合體系橋靜風穩定性研究

張新軍,胡智勇,孫雷雷

(浙江工業大學 土木工程學院,浙江 杭州 310023)

斜拉-懸吊組合體系橋是將傳統懸索橋和斜拉橋融合于一體的一種纜索承重橋梁結構形式,具有跨越能力強、結構剛度大、結構動力性能好以及造價低等特點[1]。研究表明:斜拉-懸吊組合體系橋在1 100～1 800 m跨徑范圍內可以與懸索橋競爭,尤其在1 400～1 800 m跨徑范圍內更具有優勢[2]。自1883年建成紐約布魯克林大橋以來,斜拉-懸吊組合體系橋經過140年的研究實踐,羅勃林、狄辛格、斯坦因曼、林同炎和吉姆辛等相繼提出了各自的結構體系,并在多座世界大跨橋梁的方案設計中采用[1-2]。斜拉-懸吊組合體系橋在實際工程中得到成功應用,如2016年建成通車的土耳其博斯普魯斯海峽三橋(主跨1 408 m)和我國在建的西堠門公鐵兩用大橋(主跨1 488 m)等。作為一種新型纜索支承橋梁,斜拉-懸吊組合體系橋跨度大,結構輕柔,靜風穩定性是其建設需要考慮的關鍵問題。近年來,國內外學者雖然圍繞斜拉-懸吊組合體系橋的結構體系、靜力和動力性能等問題開展了眾多的研究[2-8],但很少涉及靜風穩定性的研究。張新軍等[9]針對主跨1 400 m的吊拉組合體系橋,采用三維非線性靜風穩定性分析方法,開展了兩種主梁架設順序全過程的靜風穩定性分析。邵國攀[10]擬定主跨2 100 m超大跨度吊拉組合橋梁方案,采用基于ANSYS的非線性靜風響應分析程序對主梁采用整體鋼箱梁和分體雙箱梁兩個設計方案的靜風穩定性進行對比分析。楊進[11]針對主跨1 488 m的斜拉-懸索協作體系橋梁開展非平穩風場作用下的靜風和抖振響應分析,并揭示了靜風響應對非平穩抖振響應的影響。上述斜拉-懸吊組合體系橋的靜風性能研究都是基于法向風作用情形,即假定風垂直地吹向橋軸線。大跨度橋梁的橋位設計和現場風速觀測均表明橋梁所受強風的來流方向大多偏離橋跨法向[12],因此開展斜風作用下結構的靜風穩定性研究更具實際工程意義。當前,雖然針對斜風作用下斜拉橋和懸索橋的靜風性能已開展了數值分析和試驗研究[13-16],但對于斜拉-懸吊組合體系橋至今未見文獻報道。

為此,采用考慮靜風荷載和結構非線性的斜風作用下結構三維非線性靜風分析程序,針對主跨1 400 m的斜拉-懸吊組合體系橋設計方案進行法向風和斜風作用下結構的靜風穩定性進行分析,并揭示斜風作用對斜拉-懸吊組合體系橋靜風穩定性的影響,為該類橋梁的抗風分析提供理論指導。

1 斜風作用下結構三維非線性靜風穩定性分析程序

當前,斜風分析主要有斜風分解法和斜截面法等兩種方法[12]。前者將斜風分解為垂直和平行于橋跨方向的兩個分量,并分別計算順橋向和橫橋向的靜風荷載,最后將靜風荷載施加到結構上進行分析[3]。這是一種近似的處理方法,雖然比較適用于跨度不大的閉口扁平箱形主梁斷面,但是對于開口或開槽的主梁斷面,由于橫梁暴露引起的擋風效應會導致偏于不安全的計算結果。后者直接采用風洞試驗中測得的斜片條節段的靜風荷載六分力系數計算靜風荷載及其響應,該方法準確地考慮斜風作用對結構靜風響應的影響,筆者分析就采用該方法。斜風作用下斜拉-懸吊協作體系橋的靜風穩定性分析采用斜風作用下結構三維非線性靜風穩定性分析程序(以下簡稱3DNASA-SW),其流程如圖1所示[17]。3DNASA-SW基于斜風作用下主梁和纜索單元的靜風荷載計算模型,考慮結構及其所受靜風荷載的雙重非線性特性及三維效應,通過外層風速增量和內層靜風平衡狀態迭代的增量迭代方法搜尋結構的靜風失穩臨界狀態。計算程序中的結構三維幾何非線性分析采用CR(Co-rotational)-UL(Updated lagrangian)方法,即拖動坐標修正拉格朗日法,以有效處理大跨度橋梁結構的大位移和大轉動問題。

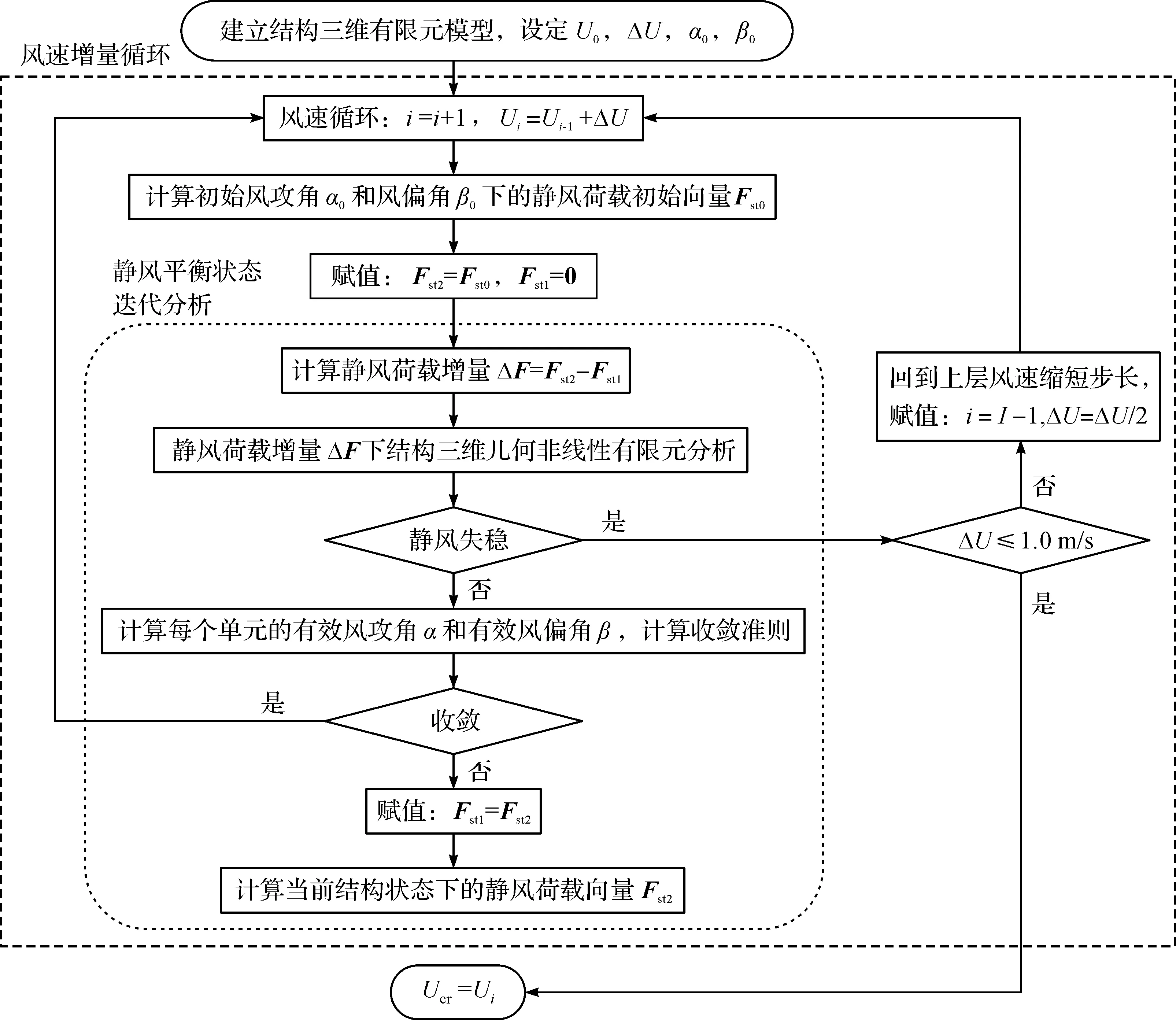
圖1 3DNASA-SW流程圖

2 橋梁及三維有限元模型簡介

圖2為一座1 400 m主跨的斜拉-懸吊組合體系橋設計方案,兩個邊跨各為319 m。主跨由618 m的懸吊段、680 m的斜拉段以及兩側各54 m的斜拉懸吊結合部組成,每個結合部設置4對交叉吊桿。主纜橫向間距34 m,吊桿間距18 m,懸吊段主纜矢跨比為1/10。斜拉索在邊跨和中跨的錨固間距分別為14 m和18 m。橋面主梁采用閉口鋼箱梁,寬36.8 m,高3.85 m。橋塔為鋼筋混凝土門式框架結構,塔高約259 m。錨碇為重力式錨碇。

圖2 斜拉-懸吊組合體系橋設計方案(單位:m)

以下分析時將圖2簡化為如圖3所示的三維有限元分析模型,當中橋面主梁、橋塔及剛性橫梁均采用空間梁單元模擬,主纜、吊桿及斜拉索則采用空間桿單元模擬。橋面主梁采用魚骨式計算模型,主梁與吊索和斜拉索之間通過剛性橫梁進行連接。塔梁之間耦合橫向自由度,墩梁之間耦合豎向和橫向自由度。

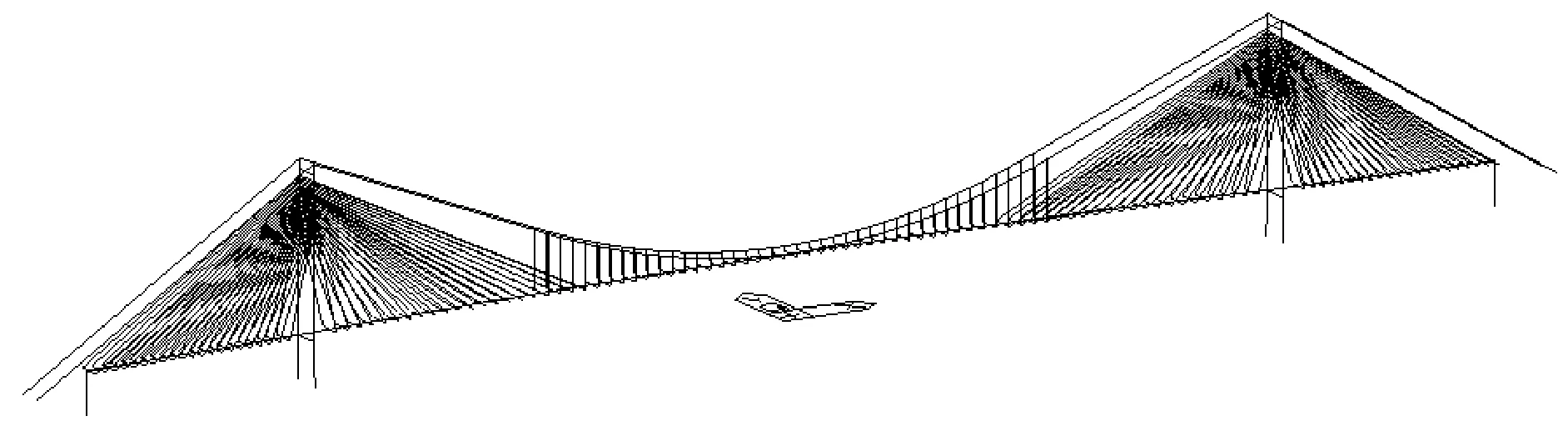
圖3 斜拉-懸吊組合體系橋三維有限元分析模型

3 斜風作用下斜拉-懸吊組合體系橋靜風穩定性分析

采用與方案橋主梁斷面形狀和尺寸極為相似的類似主梁(圖4)在斜風作用下節段模型風洞試驗測得的靜風六分力系數(圖5)[18],基于方案橋成橋階段三維有限元模型,在-3°～3°初始風攻角和0°～20°初始風偏角范圍內,采用3DNASA-SW分析了該橋的靜風穩定性。由于其余方向的靜風位移都很小,圖6中僅給出主跨跨中處主梁橫向、豎向和扭轉位移隨風速增加的變化曲線。圖6中:β0為初始風偏角;DL為橫橋向位移;DV為豎向位移;DT為扭轉角。

圖6 主梁跨中位移隨風速增加的變化規律

由圖6可知:1) 在法向風(β0=0°)和斜風(β0≠0°)作用下,主梁橫橋向、豎向和扭轉位移隨風速的增大呈非線性增長趨勢,風速增大到一定程度后主梁的豎向和扭轉位移會突然增大,當達到臨界風速后,主梁位移出現發散現象而導致結構喪失穩定性。斜拉-懸吊組合體系橋的靜風失穩形態是一種主要由主梁豎彎和扭轉耦合失穩的形態,與法向風作用下的靜風失穩形態相同,表明斜風作用并不會改變斜拉-懸吊組合體系橋的靜風失穩形態,然而會顯著影響其靜風失穩臨界風速。2) 不同初始風攻角下,主梁跨中處位移的演變規律略有不同,在負的初始風攻角下,當風速增大到一定程度后,主梁的豎向和扭轉位移變化曲線存在明顯拐點,呈現出“硬”靜風失穩特點,而在0°和正初始風攻角下則沒有明顯拐點,表現為“軟”靜風失穩特點。

為了清楚地了解斜風作用對斜拉-懸吊組合體系橋的靜風穩定性的影響,圖7給出了不同初始風攻角下靜風失穩臨界風速隨風偏角增加的變化趨勢。圖7中:實線表示3DNASA-SW計算結果;虛線表示斜風分解法的計算結果;兩者之間的差異率γ如表1所示,計算式為

表1 程序和斜風分解法計算結果的差異率

圖7 不同風攻角下靜風失穩臨界風速隨風偏角增加的變化趨勢

γ=(Ucr,procedure-Ucr,decomp)/Ucr,procedure

(1)

式中:Ucr,procedure為3DSNAA-SW計算的靜風失穩臨界風速;Ucr,decomp為斜風分解法得到的靜風失穩臨界風速,其計算式為

Ucr,decomp=Ucr,0°/cosβ0

(2)

式中Ucr,0°為法向風(β0=0°)下由3DSNAA-SW計算的靜風失穩臨界風速。

由圖7可知:不同初始風攻角下靜風失穩臨界風速隨風偏角增大的變化趨勢各不相同,在-2°和-3°初始風攻角下呈現單調遞增趨勢,在1°、2°和3°初始風攻角下則呈逐漸下降趨勢,而在-2°和-3°初始風攻角下,則呈現先下降而后緩慢增加的變化規律。因此,除-2°和-3°初始風攻角外,其余風攻角下的靜風失穩臨界風速均出現在風偏角為10°(0°、1°和-1°風攻角)、15°(2°風攻角)和20°(3°風攻角)的斜風情況下。在所計算的風攻角和風偏角范圍內,該方案橋的最小靜風失穩臨界風速為101 m/s,出現在3°風攻角和20°風偏角情況。因此,為確保橋梁結構的抗風安全性,應重視斜風作用下的靜風穩定性分析。另外,如圖7所示,各初始風攻角下程序計算得到的靜風失穩臨界風速隨風偏角增大的變化規律并非如斜風分解法所分析的余弦變化規律。由表1可知:程序和斜風分解法計算結果的差異率為-11.7%～2.9%,且隨著風偏角的增加兩者之間的差異顯著增大。除-3°風攻角外,其余風攻角下的程序計算結果均明顯小于斜風分解法計算結果,采用斜風分解法會高估結構的靜風穩定性。因此,為準確預測橋梁的靜風穩定性必須采用考慮斜風作用、靜風荷載和結構非線性的斜風作用下結構三維非線性靜風分析方法。

為了揭示斜風作用對斜拉-懸吊組合體系橋靜風穩定性的影響程度,定義斜風作用對靜風失穩臨界風速的影響率ηβ為

ηβ=(Ucr,β0-Ucr,0°)/Ucr,0°

(3)

式中Ucr,β0為初始風偏角β0下的靜風失穩臨界風速。各初始風攻角和風偏角下斜風作用對方案橋靜風失穩臨界風速的影響率如表2所示。

表2 斜風作用對靜風失穩臨界風速的影響率

由表2可知:斜風作用對斜拉-懸索組合體系橋靜風穩定性的影響存在正負效應,在非負風攻角下斜風效應將降低結構的靜風穩定性,而在負攻角下則會提高靜風穩定性,影響率為-4.7%～9.5%,不同初始風攻角下的平均影響率為-3.1%～4.6%。同時,斜風作用對靜風失穩臨界風速的影響隨著初始風偏角的增加逐漸顯著,因此需要特別關注非負攻角下較大風偏角的斜風對斜拉-懸索組合體系橋靜風穩定性的不利影響。

4 結 論

采用3DNASA-SW,以1 400 m主跨的斜拉-懸吊組合體系橋設計方案為研究對象,進行了法向風和斜風作用下的靜風穩定性分析,研究結果表明:1) 斜拉-懸吊組合體系橋的靜風失穩表現為主梁豎向彎曲和扭轉強烈耦合的失穩形態,斜風作用不會改變斜拉-懸吊組合體系橋的靜風失穩形態。不同初始風攻角下的結構靜風失穩現象有所不同,呈現出“硬”或“軟”的靜風失穩特點。2) 不同初始風攻角下斜拉-懸吊組合體系橋靜風失穩臨界風速雖然隨風偏角增大的變化趨勢各不相同,但都不是如斜風分解法所述的余弦變化規律,最小靜風失穩臨界風速大多出現在斜風作用情況。程序分析與斜風分解法計算結果的差異率為-11.7%～2.9%,且以負值為主。除-3°風攻角外,程序計算結果均明顯小于斜風分解法計算結果,斜風分解法將高估斜拉-懸吊組合體系橋的靜風穩定性。3) 斜風作用對斜拉-懸索組合體系橋的靜風穩定性存在著正負影響,影響率為-4.7%～9.5%,尤其要注意非負攻角下較大風偏角斜風的不利影響。為準確預測斜拉-懸吊組合體系橋的靜風穩定性,必須采用考慮靜風荷載和結構非線性的斜風作用下結構三維非線性靜風分析方法。