“模型思想”在2022年新高考全國Ⅱ卷中的應用探析
福建師范大學附屬福清德旺中學 (350319) 周 丹
福建省福清市進修學校 (350300) 林新建
數學建模是對現實問題進行數學抽象,用數學語言表達問題、用數學方法建構模型解決問題的素養.數學模型是借用數學的語言講述現實世界中的數量、圖形有關的故事,使數學走出了自我封閉的世界,構建了與現實世界的橋梁.在解題過程中,“模型思想”的建立,能幫助我們更好地挖掘模型或者建構模型,從而將復雜的問題化歸轉化為簡單的數學模型進行求解,進一步培養學生的核心素養,在教學中具有實際的意義.以下就“模型思想”在2022年新高考全國Ⅱ卷中的應用作一探析,以饗讀者.
一、挖掘模型
應用“模型思想”在題中挖掘所蘊藏的數學模型,借助找出的數學模型簡化運算,將問題輕松解決.
A.-6 B.-5 C.5 D.6



評析:本題中強調用數學的眼光去直觀想象并進行數學抽象,一步步地抽象出菱形模型,是“模型思想”的應用,整個過程進行邏輯推理,培養了學生的數學眼光、數學思維和數學核心素養.
例2 (第12題)若x,y滿足x2+y2-xy=1,則( ).
A.x+y≤1 B.x+y≥-2
C.x2+y2≤2 D.x2+y2≥1




分析:由|MA|=|NB|可知,線段MN中點與線段AB中點重合,這樣就可以將問題抽象為中點重合模型進行求解.


評析:本題通過數學抽象,抽象出中點重合的模型,注重對數學運算的考查,中點模型的給出可以簡化運算,而圓錐曲線簡化運算實際上是基于數學抽象和邏輯推理下的運算簡化,進一步也培養了學生的數學抽象和邏輯推理素養.
二、建構模型
應用“模型思想”,借助一些現有模型特征構建滿足題意的新模型,或通過觀察、分析數學式子特征,建構適當的模型,幫助問題更好、更快地解決.

A.-3 B.-2 C.0 D.1




評析:本解法先通過對模型的初步識別,發現這個模型與兩角和余弦公式的模型類似,由此受到啟發,通過待定系數法建構合理的建模,實現從特殊到一般,再從一般到特殊的轉化,實際上也是數學抽象的培育過程.
例5 (第22題)已知函數f(x)=xeax-ex.
(1)當a=1時,討論f(x)的單調性;
(2)當x>0時,f(x)<-1,求a的取值范圍;
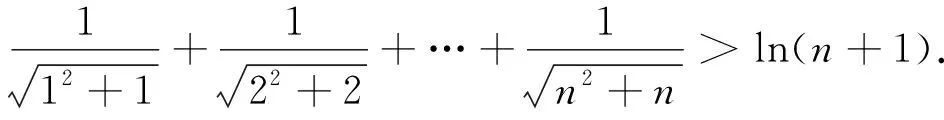


評析:引導學生分析觀察數學式子,猜測探究適當的數學結論,給出解釋或證明,培養學生直觀想象,數學抽象,邏輯推理,數學建模核心素養.
三、結語
“模型思想”的培養,不止可以幫助學生快速地挖掘或建構合理的模型來解決問題,從而有效地簡化求解途徑,還能通過數學建模的過程,提高學生發現和提出問題的能力、分析和解決問題的能力.在“模型思想”的培養過程中,教師要引導學生用數學的眼光去觀察,用數學的思維去思考,用數學的語言去概括,進一步使學生掌握必備的基礎知識和關鍵能力,培養學生的數學抽象、邏輯推理、數學建模、直觀想象、數學運算等素養.

