一道三角最值問題的多解及拓展

廣東省佛山市羅定邦中學 (528300) 范光玉

解三角形問題的常用解題思路是利用正余弦定理,實現邊角的互化后進行求解;其次三角形作為平面圖形,其自身具有豐富的幾何性質,我們還可通過幾何的視角來進行求解.本文對2022年新課標Ⅰ卷第18題的多解進行分析并將問題拓展到一般結論.

一、題目呈現

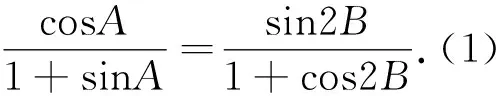
本題的主題干較為簡單,考察二倍角等三角恒等變換的相關公式獲得△ABC三個內角間的關系,在此基礎上求解第(1)問就較為簡單;本題的難點主要集中在第(2)問,所求式考察了三個變量間的關系,觀察其結構發現其為齊次式,我們可以通過構造邊與邊之間的比例進行消元;其次,也可通過邊化角后構成比例關系進行消元.

二、多解分析

對于第(2)問,主題干是關于角的關系,為此自然想到利用邊化角來進行求解.

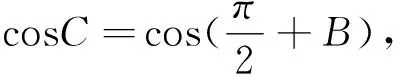
評注：上述解法將所有變量都用cosB來表示,實現了化簡的目的,再利用基本不等式或利用“對勾函數”的性質即可求解.

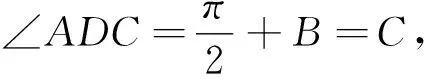
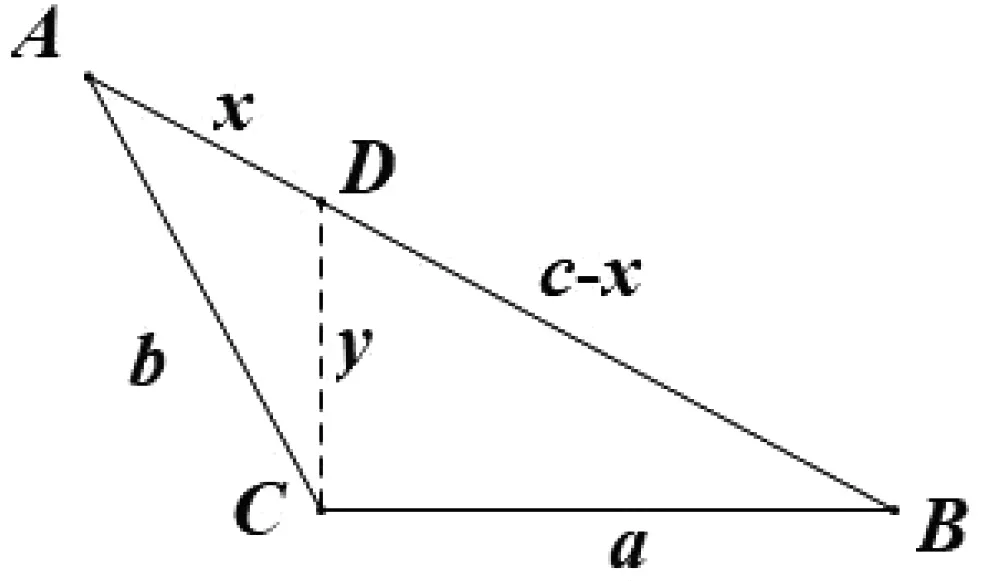
圖1

評注：本題的核心是發現三角形相似,從而獲得邊之間的關系,再利用勾股定理實現了消元,再利用齊次化的思想求解.

解法三：(利用幾何性質及邊化角求解)

如圖2,在圖1的基礎上延長BC,過點A作BC延長線的垂線,垂足為E.在解法二的基礎上可知在ΔAEC中,∠EAC=B,故可得AE=bcosB,CE=bsinB.在ΔAEB中,AE=csinB,CE+a=ccosB.結合正弦定理即得sin2C=cos2B,sin2A=cos22B成立,后續解法同解法一.

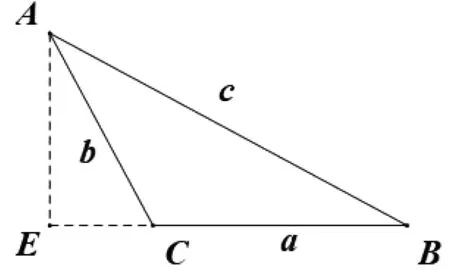
圖2

三、問題拓展

通過對上述解答過程的分析,我們可將原問題進行拓展.

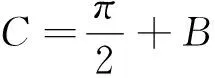
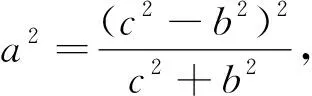
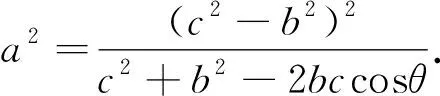
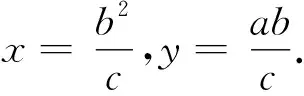
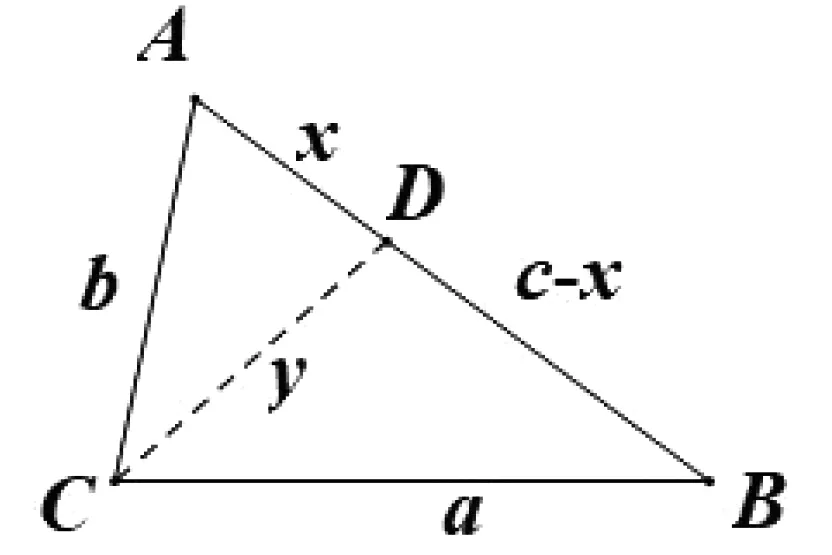
圖3