一類數列型不等式問題的證法探究

甘肅省慶陽市鎮原縣屯字中學 (744502) 郭宏剛

以基礎函數“lnx”作為題設背景的數列型不等式證明一類問題,是出現在近年高考或各地模擬考試中的熱點題型,這類問題常與導數應用緊密聯系,把與lnn(n∈N*)相關聯的數列型不等式的證明設置在試題的最后一問,證題時利用前面小問中的導數研究函數單調性結論來證明.下面以一道高三階段性測試題來探究一類數列型不等式的證明方法.

1 試題呈現

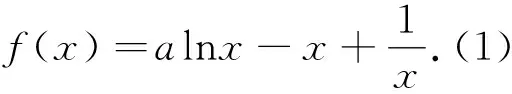
該題以基本函數“lnx”為題設背景,其中第(2)小題是證明數列型不等式問題,這一小題解答的基本路徑是:逆向分析,尋找與所證不等式等價的不等式,通過構造函數,運用導數知識推得基礎函數的不等式,進而將結論予以賦值轉化為數列的不等關系,最后利用數列比如裂項、累加等方法,或運用“放縮法”證得數列不等式.

2 試題解答

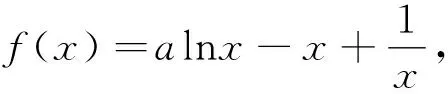
①當a≤0時,易知當時當x>0時,f′(x)<0,此時f在(0,+∞)上單調遞減.

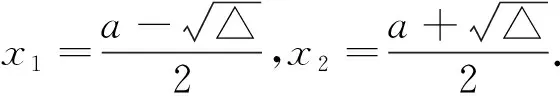
當x變化時,f′(x),f(x)變化情況列表如下:

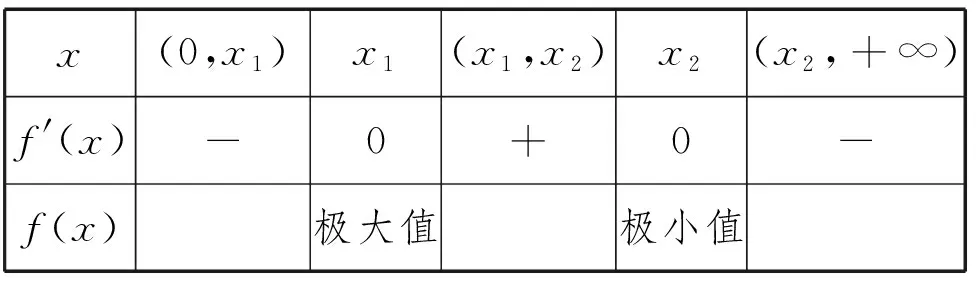
x(0,x1)x1(x1,x2)x2(x2,+∞)f'(x)-0+0-f(x)極大值極小值

綜上所述,當a≤2時,f(x)在(0,+∞)上單調遞減;當a>2時,f(x)在(0,x1),(x2,+∞)上單調遞減,在(x1,x2)上單調遞增.

下面重點探究第(2)問中數列型不等式的證明.

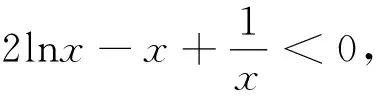
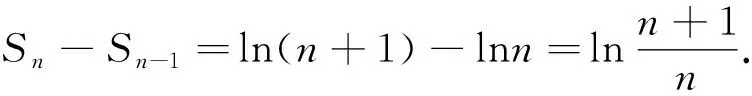
點評：證法1首先將所證的數列不等式進行逆向分析,結合其結構形式的特點,利用由(1)函數單調性所證得的不等式證明.

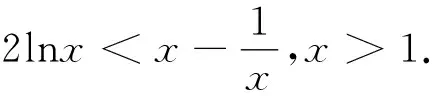
點評：證法2在由(1)函數單調性所證得的不等式的基礎上,通過賦值、累加證得所證不等式.

為了介紹證法3,這里給出對數均值不等式.

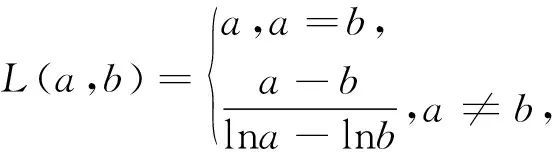
對數均值不等式證明詳見文[1].

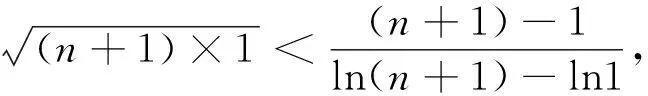
3 變式探究

若稍加改變一下題設中的函數表達式,第(2)小題中所證的數列型不等式不變,則有:

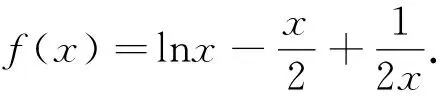
(1)解關于x的不等式f(x)>0;

解析：(1)易得f(x)>0的解集為(0,1).

(2)同上述測試題的證法.若將題設條件中的函數式改為關于基礎函數“ex”的不等式,所證的數列型不等式不變,則有:

變式2 (2022年新高考Ⅱ卷的第22題)已知函數f(x)=xeax-ex.

(1)當a=1時,討論f(x)的單調性;

(2)當x>0時,f(x)<-1,求a的取值范圍;

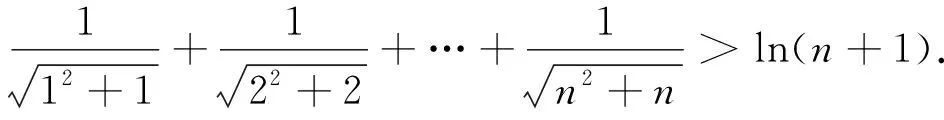
由此可以看出,上述測試題的第(2)小題其實就是該高考題的第(3)小題.在強調高考命題深化改革的今天,通過改編、整合等手段來給予以往高考真題新的生命,從而演變為新的試題,已成為高考命題的一種常態化趨勢.以“題”為鑒,這就啟示我們在復習備考的過程中重視對以往高考真題的深層次探究,通過探究,分析高考命題和考查的思想方法、本質及學科核心內容,關注命題者的意圖、解題需要的能力和科學的思維方法,使復習跳出題海,并“打磨利器,有的放矢”,利用對以往高考真題檢驗復習效果,使復習備考“擇高處立,向闊處行”.

解析：(1)f(x)在(0,+∞)上單調遞增.

(2)a=1.

4 方法總結

對比上面三種證法,利用對數均值不等式(即證法3)證明數列型不等式,可以避開求導、應用導數研究函數單調性等復雜過程,簡捷明了、操作性強,是證明數列型不等式這一類問題的通性通法.

運用對數均值不等式證明與lnn(n∈N*)相關聯的數列型不等式的方法步驟是:分析→選取→賦值→得證,即:①分析研究所證數列不等式的結構特點;②合理選取對數均值不等式鏈中的某個不等式;③對選取的對數均值不等式鏈中的不等式中的a,b恰當賦值,有時結合放縮技巧;④證得不等式.

對典型試題解法的探究,就是指對問題從不同視角來審視,以不同的切入點探究問題,其實質是對試題的“二次開發”.通過對試題的剖析和思考,展開問題的來龍去脈和知識間的縱橫聯系,站在一定的高度去思考問題,突出數學本質,使知識達到融會貫通,使思維得到升華,進而優化數學思維品質.