幾何直觀在解決小學有余數除法問題中的嘗試
——以“進一”和“去尾”為例
麥小燕
一、 引言
幾何直觀主要是指運用圖表描述和分析問題的意識與習慣。利用圖表分析實際情境與數學問題,探索解決問題的思路,有助于建立形與數的聯系,構建數學問題的直觀模型,把握問題的本質,明晰思維的路徑。
二、 有余數除法解決問題的教學現狀
目前有余數除法解決問題的教學不容樂觀。學生存在的問題主要有:不理解題意,生搬硬套解題模式,常常見到題目中的“至少”就“進一”,見到“最多”就“去尾”,但不知道為何要“進一”和“去尾”;將數學與生活聯系起來的意識不夠強,導致對余數的“取”“舍”模棱兩可。
而教師日常只關注本年級“有余數除法解決問題”知識點教學,沒有對整個小學階段出現的有余數除法解決問題知識點進行系統性研究。在例題的教學中,忽略了畫圖策略的運用,沒有讓學生從根本上去理解余數的“取”與“舍”,特別是在教授高年級的有余數除法問題時,引導花費時間較少,講解也不到位,多半是套解題模式。所以,小學有余數除法解決問題的教學隨意低效,長此以往,學生將疲憊不堪,思維能力也得不到提升。
三、 幾何直觀在解決有余數除法問題中的必要性
在有余數除法解決問題(以“進一”法和“去尾”法為例)的教學中,借助幾何直觀把有余數除法的應用問題轉換成直觀圖,厘清數量關系,可以幫助學生從根本上去理解問題、解決問題。另外,借助幾何直觀有意識地溝通數、形之間的聯系,把“數形結合”有意識地滲透在學生解決問題的過程中,有助于培養學生幾何直觀核心素養,提高學生的數學思維品質。
(一)幾何直觀助力數學信息的正確解讀
正確地解讀數學信息,是有效建立數量關系模型的前提,幾何直觀能有效地幫助學生正確解讀數學信息。在有余數除法解決問題的教學中,我們要充分利用示意圖來幫助學生解讀信息的含義。教學時,我們首先要引導學生將用文字語言敘述的數學信息轉化為直觀示意圖。其次,通過示意圖讓學生分析圖形所代表的數量關系,并進一步從具體的圖形與圖形之間找到信息與信息的聯系,從而建立信息與問題之間的數量關系模型。例如,人教版小學數學二年級下冊第68頁的第8題:

在這道題中,學生知道各種花的數量和扎成一束花需要每種花的數量,但是往往因為不理解信息“用7枝月季花、3枝百合、2枝郁金香扎成一束”與問題“這些花最多可以扎成幾束這樣的花束”之間的數量關系模型而出錯。這時,我們引導學生將信息和問題轉化成示意圖(如下圖),借助示意圖,學生就能直觀地建立一束花的模型,即7枝月季花、3枝百合、2枝郁金香為一束,缺一不可。這樣就能更好幫助學生理解“最多能扎成幾束”只能以數束最少的為標準。當學生弄清楚了這一信息后,這道題就迎刃而解了。
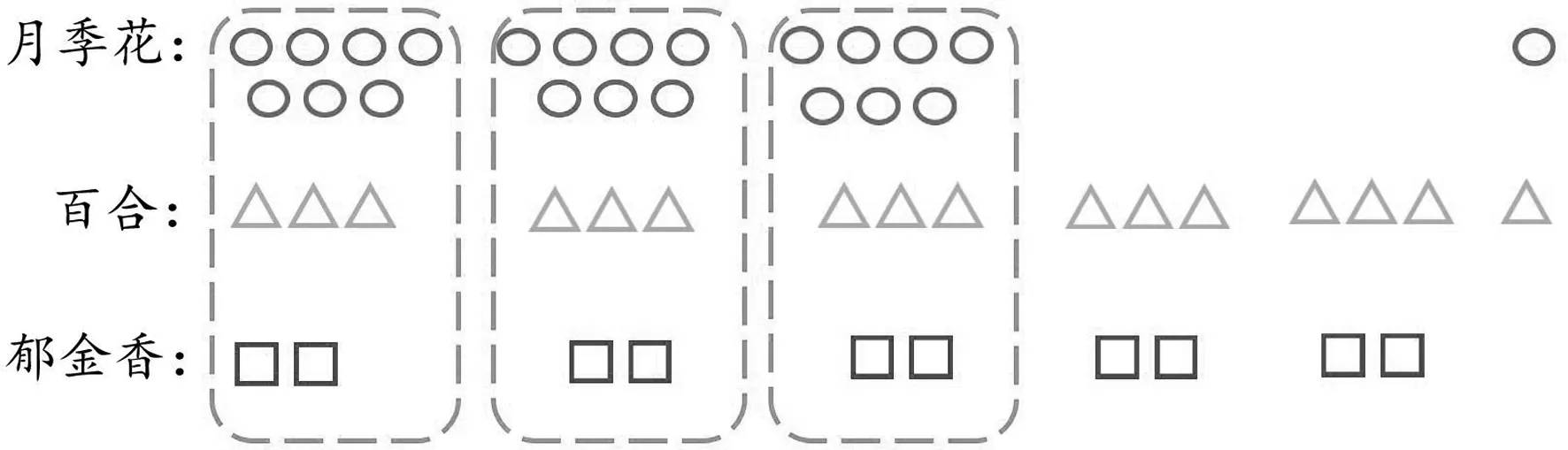
(二)幾何直觀明晰余數的“取”與“舍”
理解余數的“取”與“舍”是構建有余數除法應用問題數量關系模型的關鍵環節。在實際教學中,我們借助幾何直觀來表示有余數除法問題,分析和理解余數是“取”還是“舍”,從而解決問題。例如,人教版小學數學二年級下冊第65頁的例5:

在以往的教學中,有不少學生在列出除法算式22÷4=5(個)……2(塊)后,認為答案是5個,把剩下的2塊就忽略了。這時,我們引導學生通過畫直觀示意圖來理解余數是“取”還是“舍”。“每個盒子最多裝4塊”可以表示成“④”,“不滿4塊”的用“△”表示,如下圖:

借助示意圖,學生可以清晰地理解算式“22÷4=5(個)……2(塊)”中“5個”指的是有5個盒子“裝滿了4塊”,余數“2塊”指余下的2塊沒有裝滿一盒,但是也要再用一個盒子裝,這時余數要“取”,所以至少是5+1=6(個)。
通過用兩種不同的圖形代表“商”和“余數”,把有余數除法問題轉換成直觀示意圖,讓學生結合圖形去理解文字信息、算式所表達的意思,使學生對余數的“取”與“舍”理解得更透徹。
四、 幾何直觀在各學段有余數除法解決問題中的運用策略
在借助幾何直觀解決各學段有余數除法問題的教學過程中,我們根據學生的年齡特點,在不同學段采用不同的數形結合策略。
(一)先“形”后“數”
第一、二學段的學生,他們心理發展的特征決定了他們的思維以具體形象思維為主,邏輯思維尚處于萌芽階段,因此這一階段適合先“形”后“數”。但應注意在利用“形”學習知識的過程中,應適時、適當地引導學生逐步歸納,進而上升到理性認識,為培養學生的邏輯思維作準備。
例如,人教版數學一下第46頁例7:
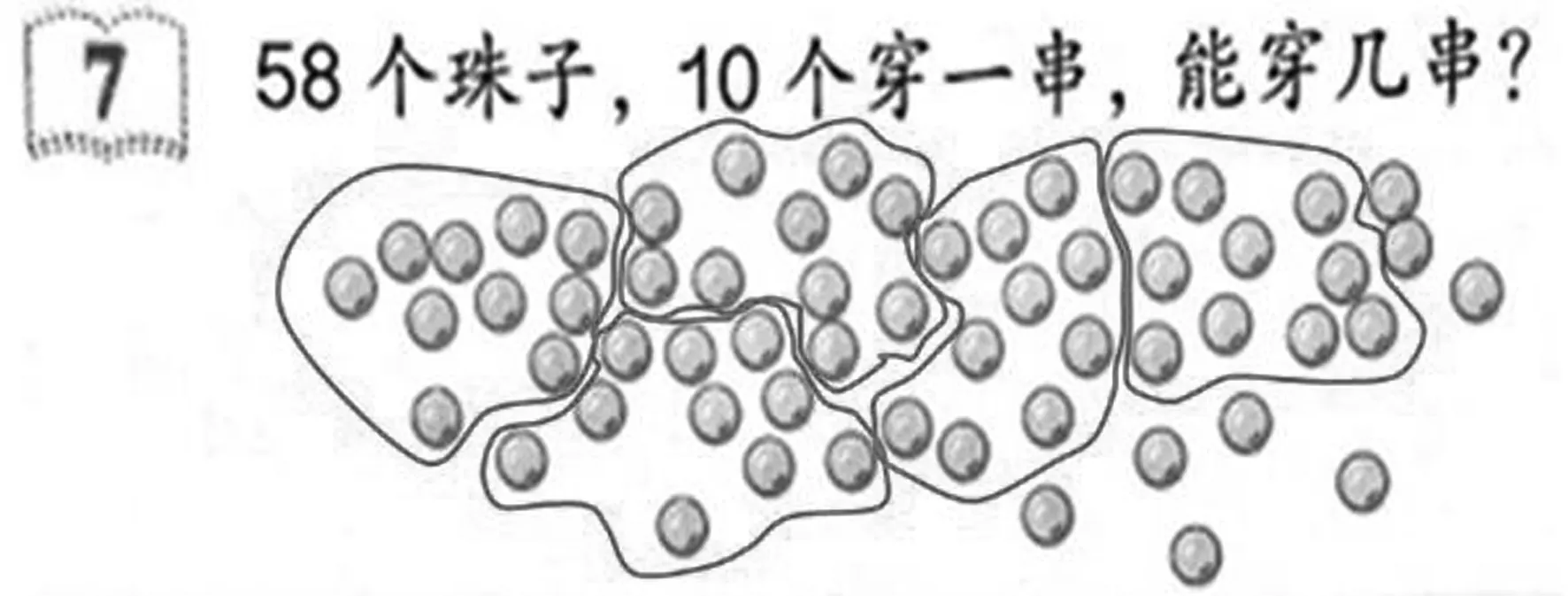
根據一年級學生的思維特點,教材中的題目已經是數形結合,通過圈一圈的方法就能直觀地得出穿幾串,剩幾個。但是邏輯思維能力較強的學生會采用列式計算:58-10-10-10-10-10=8。因此在教學的過程中,我們可以先圈一圈,再根據直觀示意圖列出算式,幫助學生從具體認知上升到理性認知。
又如,人教版小學數學三年級下冊第27頁例8第2問:
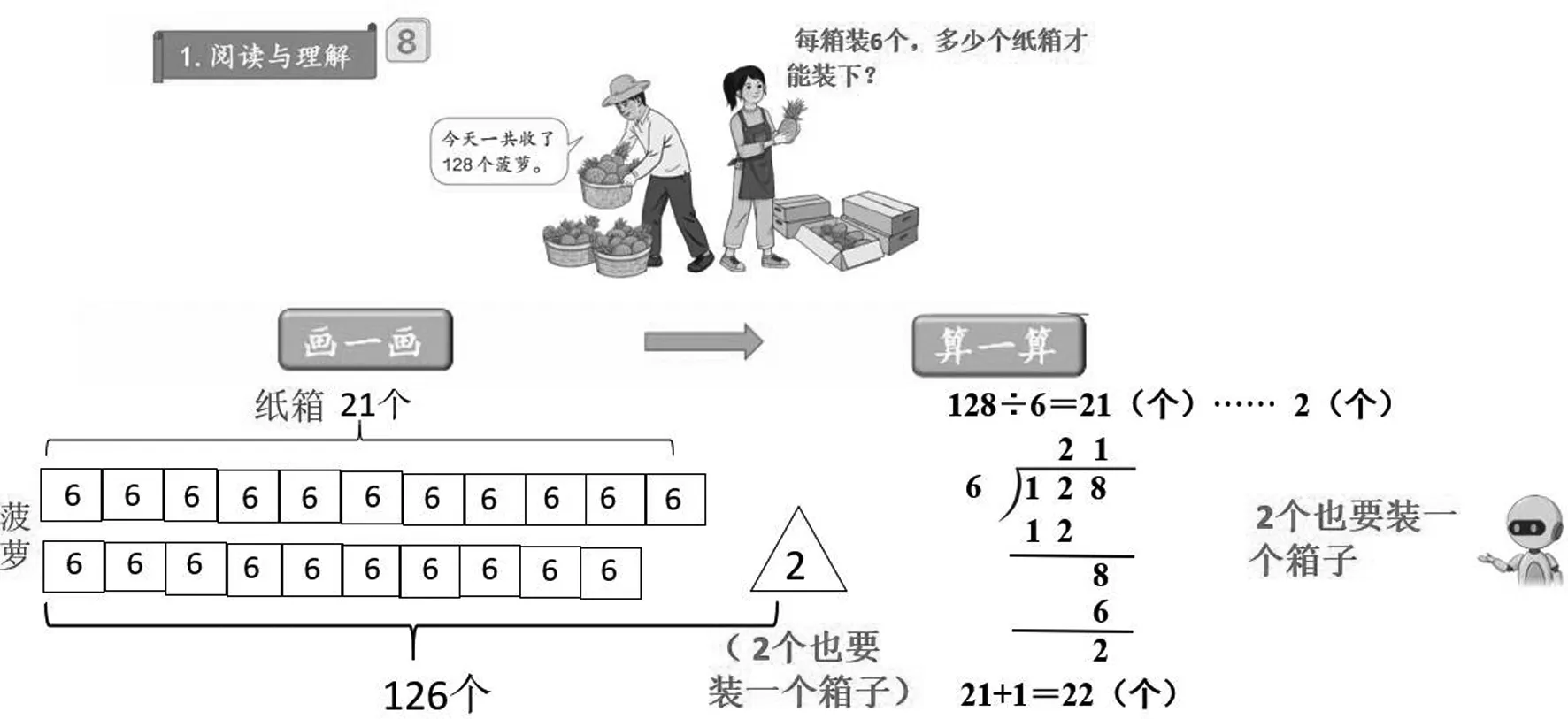
借助示意圖,幫助學生直觀地理解為什么要加1,因為剩余的2個菠蘿也要另裝1個箱子,所以22個箱子才能裝下。與此同時,引導學生根據直觀示意圖列出算式。
從上面的兩個例子可以發現,第一、二學段的有余數除法解決問題的教學模式是:審題—畫圖—列式,先“形”后“數”,幫助學生從具體認知逐步上升到理性認知。
(二)先“數”后“形”
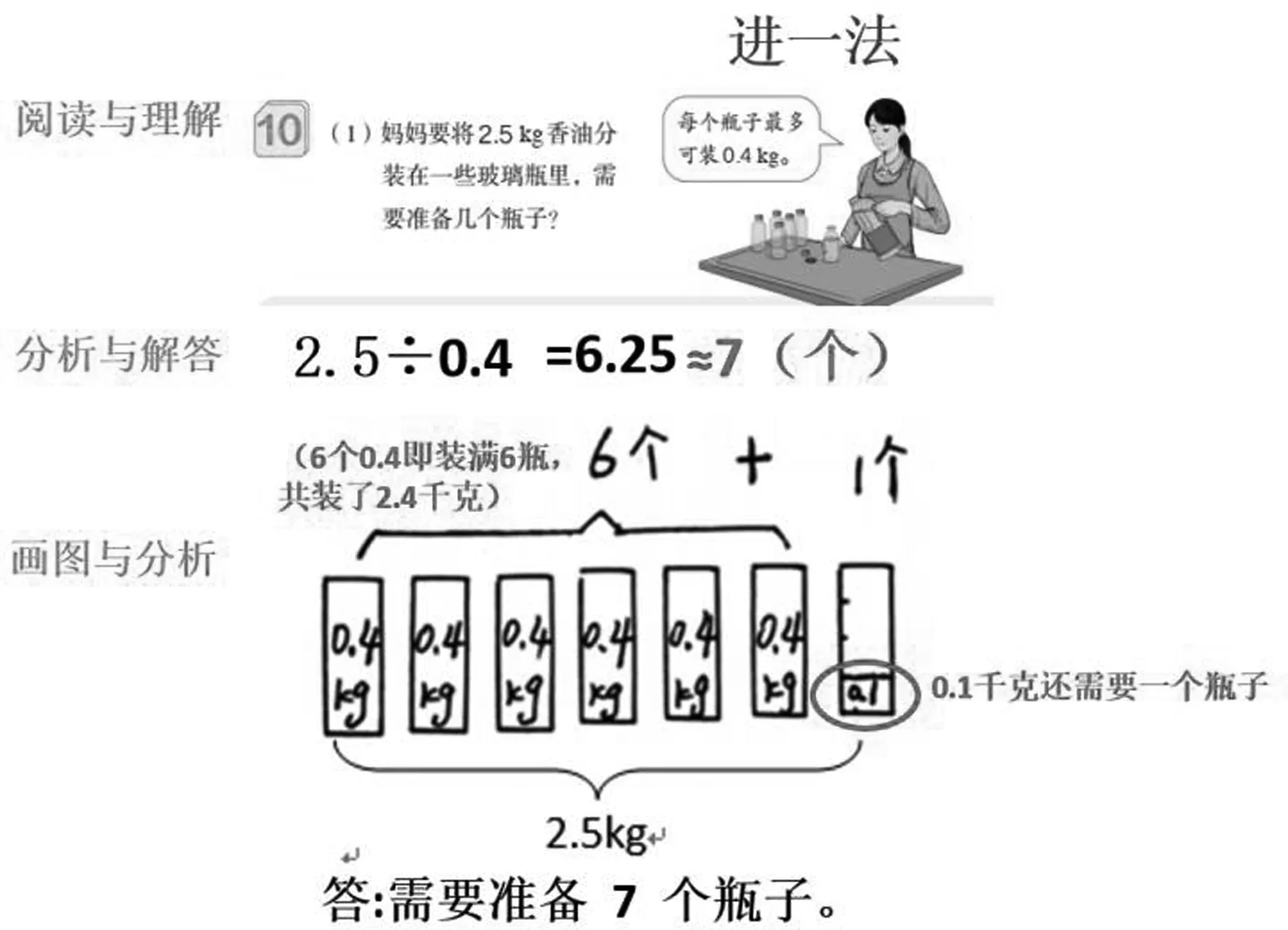
有了第一、二學段的幾何直觀基礎,學生邏輯思維力已有一定程度的發展,在第三學段的有余數除法應用問題的教學中,應逐漸過渡到先“數”后“形”,把“形”真正放在主要地位。例如,人教版五年級上冊第3單元小數除法例10:
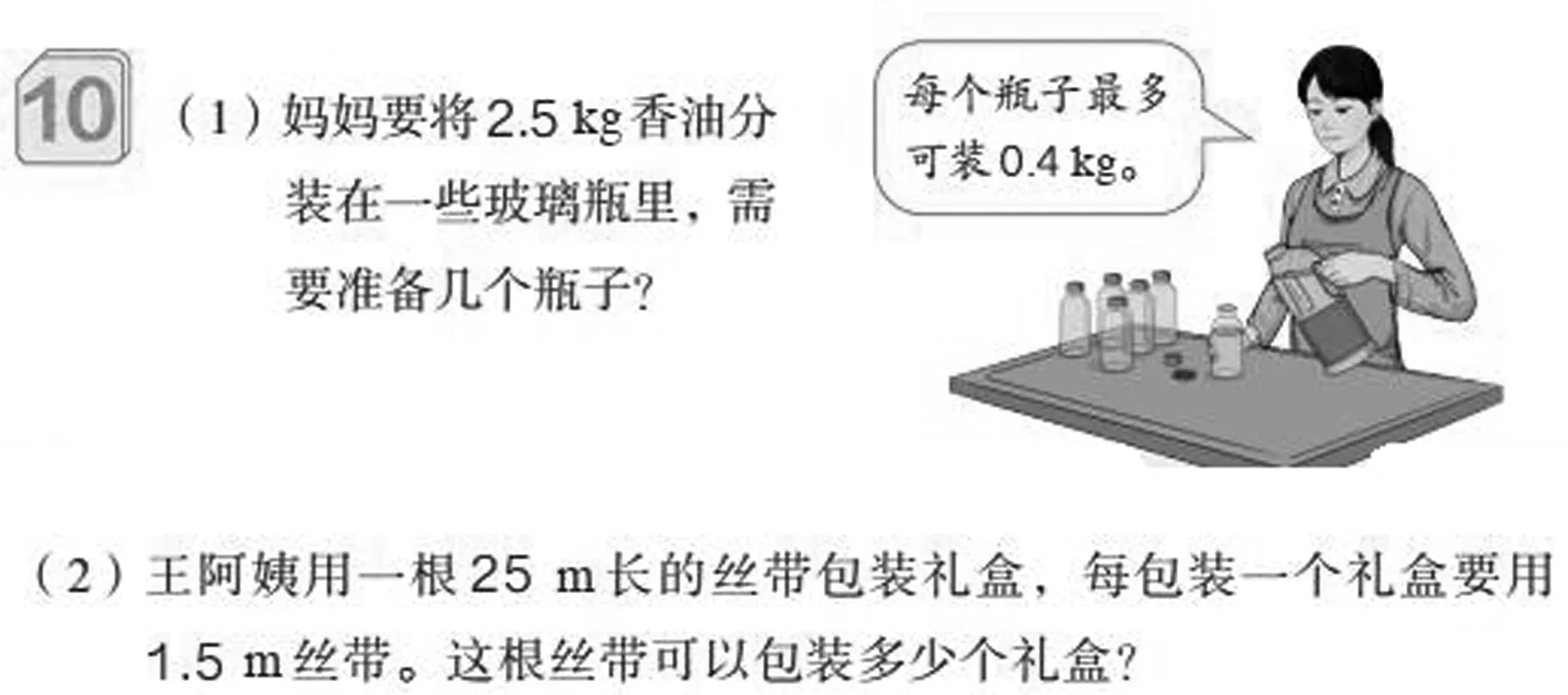
教材強調“在解決實際問題時,要根據實際情況取商的近似值”;初步讓學生學會從數學的角度發現問題和提出問題,綜合運用數學知識解決簡單的實際問題,增強應用意識,提高實踐能力;獲得分析問題和解決問題的一些基本方法,體驗解決問題方法的多樣性,發展創新意識。
因此,在教學中,教師可放手讓學生自由選擇“數”與“形”的先與后,或者二者任選其一。
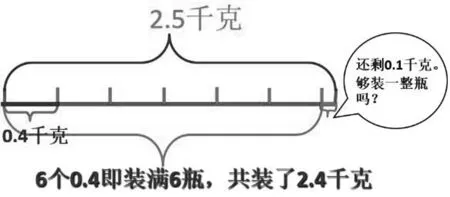
在例10的第1小題的教學中,先讓學生閱讀理解題目然后再列式計算:先求2.5里面有幾個0.4,2.5÷0.4=6.25(個),再引導學生探究為什么一共需要7個瓶子才能裝完。對于理解有困難的學生,我們通過畫直觀示意圖讓學生直觀地理解:6個瓶子只裝了2.4千克的油,剩下的0.1千克也需要裝在1個瓶子里,這樣才能把香油裝完。也可以通過畫線段圖幫助學生理解,同樣可以直觀觀察到剩下的0.1千克油沒有裝滿一瓶,也需要另裝在一個瓶子里。因此,不管小數部分是幾,都要向個位進1,變成7,所以需要7個瓶子。
第(2)題的教學也是先讓學生理解題目,學生獨立列式計算解答,再通過畫圖的方式幫助學生理解小數部分“舍”還是“入”的取值問題。通過畫圖讓學生直觀地觀察到16個1.5米是24米,剩下的1米不夠包裝一個盒子。因此,要用“去尾法”把小數部分“舍”去,所以這根絲帶可以包裝16個盒子。

從以上兩個例子可以發現,第三學段有余數除法解決問題的教學模式是:審題—列式—畫圖,先“數”后“形”,通過“形”幫助學生更直觀地理解取值問題,而不能機械地使用“四舍五入”法,要根據具體情況確定“舍”與“入”。
(三)從不同的角度考慮“數”與“形”的先后
關于幾何直觀教學策略中,對于“數”與“形”的先與后,除了根據學生的年齡特點,也可以從以下方面分析決定:
(1)看學生的層次。形象思維、邏輯思維較弱的學生,可先“形”后“數”;較好學生可先“數”后“形”。
(2)看教材“新舊”程度。新內容先“形”后“數”,后續教材讓學生利用“遷移規律”先“數”后“形”。
五、 結論
綜上所述,在有余數除法解決問題的實際教學中,我們要有意識地運用幾何直觀的方法,尋求解決問題的方法。幾何直觀中“數”與“形”的先與后,應根據學生思維的發展特點而定,使形象思維和邏輯思維相互促進、協調發展,讓具有不同思維特征的學生實現個性化的發展。

