基于專題研究課發(fā)展代數(shù)推理能力*
——以“5.4二次函數(shù)與一元二次方程(1)”為例

陳 卓

? 南京師范大學(xué)附屬中學(xué)江寧分校

從推理類型來看,初中階段的推理有幾何推理和代數(shù)推理．代數(shù)推理側(cè)重數(shù)和式或數(shù)量關(guān)系的變形及轉(zhuǎn)換,相對比較抽象,代數(shù)推理是學(xué)生數(shù)學(xué)思維向更高層次發(fā)展的必備能力,教材也提供了豐富的代數(shù)推理素材,因此很有必要在初中階段點面結(jié)合、系統(tǒng)推進,逐步滲透代數(shù)推理.通過課題組研究發(fā)現(xiàn),在函數(shù)教學(xué)中滲透代數(shù)思維培養(yǎng)學(xué)生推理能力非常有意義.筆者執(zhí)教了義務(wù)教育蘇科版數(shù)學(xué)教材九年級下冊第五章第4節(jié)“二次函數(shù)與一元二次方程”的專題研究課,借此談一談學(xué)生代數(shù)推理能力的培養(yǎng)問題.

1 代數(shù)推理視角下的內(nèi)容分析

1.1 挖掘內(nèi)容中的推理資源

教材從“函數(shù)值何時為0”著手,探索二次函數(shù)與一元二次方程的關(guān)系,通過函數(shù)圖象揭示一元二次方程解的幾何意義.以“特殊—一般”“具體—抽象”的路徑逐步推進,通過“數(shù)”和“形”的對比感受函數(shù)與方程之間的聯(lián)系,這樣的設(shè)計符合學(xué)生認(rèn)知規(guī)律,也符合問題探究的一般規(guī)律.結(jié)合教材,在問題情境導(dǎo)入上,以學(xué)生熟悉的命題為切入口:(1)解一元一次方程x+1=0;(2)畫一次函數(shù)y=x+1的圖象;(3)說x+1=0與y=x+1的聯(lián)系.仿照以往幾何推理的經(jīng)驗進行說理,這樣就使解方程中演繹推理格式的得出更加自然,模仿“∵……,∴……”,依據(jù)寫在結(jié)論后面括號里的方式去表達(dá)x+1=0與y=x+1之間的聯(lián)系.這樣可以有效促進學(xué)生理解函數(shù)和方程內(nèi)容中演繹推理的表征,培養(yǎng)學(xué)生代數(shù)推理能力.

1.2 關(guān)于教學(xué)目標(biāo)的落實

探索并獲得二次函數(shù)的圖象與x軸的三種位置關(guān)系和一元二次方程根的三種情況的對應(yīng)關(guān)系是本節(jié)課的教學(xué)重點,在教學(xué)過程中,學(xué)生通過“思考—探索—嘗試—歸納”,自主參與知識的發(fā)生、發(fā)展和形成過程,深刻理解轉(zhuǎn)化思想和數(shù)形結(jié)合思想,發(fā)展學(xué)生的推理能力.同時,使學(xué)生真正成為學(xué)習(xí)的主體,從“被動學(xué)會”變成“主動會學(xué)”.

2 教學(xué)實踐

2.1 溫故知新

(1)解一元一次方程x+1=0.

(2)畫一次函數(shù)y=x+1的圖象,并指出函數(shù)y=x+1的圖象與x軸有幾個交點.

(3)一元一次方程x+1=0與一次函數(shù)y=x+1有什么聯(lián)系?

設(shè)計意圖：讓學(xué)生通過對新知識的思考,梳理舊知識,起到承上啟下之效,同時,培養(yǎng)學(xué)生“一以貫之”的數(shù)學(xué)思維品質(zhì).從“數(shù)”的角度,方程的根是使函數(shù)值為0的自變量的值;從“形”的角度,方程的根是函數(shù)圖象與x軸公共點的橫坐標(biāo).仿照以往幾何推理的經(jīng)驗進行說理,促使學(xué)生理解函數(shù)和方程內(nèi)容中演繹推理的表征．

2.2 探索活動

活動1：畫出二次函數(shù)y=x2-2x-3的圖象,解決下列問題.

(1)y=x2-2x-3的圖象與x軸有公共點嗎?如果有,求出公共點的橫坐標(biāo).

(2)當(dāng)x取問題(1)中公共點的橫坐標(biāo)時,相應(yīng)的函數(shù)值分別是什么?

(3)從關(guān)系式來看,二次函數(shù)y=x2-2x-3成為一元二次方程x2-2x-3=0的條件是什么?

(4)結(jié)合二次函數(shù)的圖象,直接說出x2-2x-3=0的根.

設(shè)計意圖：從一個特例展開二次函數(shù)與一元二次方程關(guān)系的研究,讓學(xué)生感受研究的過程與前面所學(xué)知識的一致,并通過圖象進一步揭示函數(shù)與方程之間的關(guān)系.用幾何推理的經(jīng)驗、思維過程的說理,培養(yǎng)代數(shù)推理能力.

活動2：任意寫出一個二次函數(shù),仿照剛才的研究自主探索該二次函數(shù)與其對應(yīng)的一元二次方程的關(guān)系.

(1)結(jié)合多次分析,你能歸納出任意二次函數(shù)與其對應(yīng)的一元二次方程的關(guān)系嗎?

(2)結(jié)合多次分析,你能歸納出二次函數(shù)的圖象與x軸的位置關(guān)系中起關(guān)鍵作用的要素嗎?

設(shè)計意圖：學(xué)生通過類比,進一步認(rèn)識二次函數(shù)與對應(yīng)的一元二次方程的關(guān)系,在“二次函數(shù)的圖象與x軸的位置關(guān)系”和“一元二次方程的根的情況”之間形成演繹推理關(guān)系,并在多個例子的基礎(chǔ)上,歸納(這是合情推理)得到一般性的結(jié)論.

注意引導(dǎo)學(xué)生感受代數(shù)推理的必要性和深刻性,并總結(jié)“活動2”,形成如圖1所示的板書.

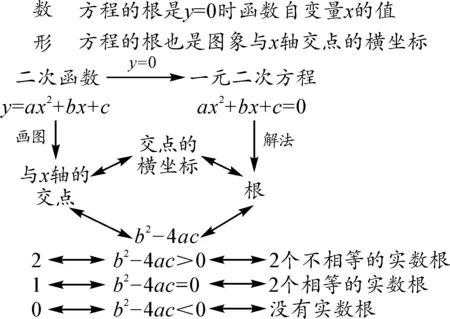
圖1

2.3 例題教學(xué)

例題不畫圖象,判斷二次函數(shù)y=-x2+5x-8的圖象與x軸是否有公共點.

解：因為一元二次方程-x2+5x-8=0根的判別式b2-4ac=52-4×(-1)×(-8)=-7<0,所以方程-x2+5x-8=0沒有實數(shù)根.

故二次函數(shù)y=-x2+5x-8的圖象與x軸沒有公共點.

設(shè)計意圖：進一步理解函數(shù)與方程互相轉(zhuǎn)化的思想,同時通過板書的展示感受推理的過程.

2.4 鞏固練習(xí)

(1)方程x2+4x-5=0的根是______,則函數(shù)的圖象與x軸交點有______個,其坐標(biāo)是______.

(2)下列函數(shù)的圖象中,與x軸沒有公共點的是( ).

A.y=x2-xB.y=x2-2

C.y=-x2+6x-9 D.y=x2-x+2

(3)已知二次函數(shù)y=x2-4x+k+2的圖象與x軸有公共點,求k的取值范圍.

設(shè)計意圖：通過鞏固練習(xí)加深學(xué)生對知識的理解,并根據(jù)反饋幫助學(xué)生理清思路,尋找解決問題的途徑,從而提高演繹推理能力．

2.5 課堂小結(jié)(略)

3 教學(xué)思考

3.1 建立“教學(xué)活動”與“代數(shù)推理”的關(guān)聯(lián)

通過數(shù)學(xué)活動,認(rèn)識到二次函數(shù)和一元二次方程之間存在的關(guān)系.關(guān)注三個層面:一是從學(xué)生已有知識去構(gòu)建二次函數(shù)與一元二次方程的關(guān)系,在構(gòu)建聯(lián)系的過程中培養(yǎng)代數(shù)推理能力;二是從學(xué)生既有經(jīng)驗畫圖推理二次函數(shù)與一元二次方程的知識點;三是從課堂操作實踐推理歸納總結(jié)難點.在學(xué)習(xí)二次函數(shù)與方程時,強化點的坐標(biāo)與方程的根的對應(yīng)關(guān)系,幫助學(xué)生更好地直觀感受數(shù)形結(jié)合.

3.2 整體設(shè)計“例題示范”與“作業(yè)強化”

通過選擇合適的例題進行板書示范和設(shè)計有代表性的作業(yè)培養(yǎng)代數(shù)推理能力.例題教學(xué)中,筆者選擇多名學(xué)生演板,然后讓學(xué)生交流做法,優(yōu)化過程,糾正錯誤.學(xué)生在解決問題的過程中培養(yǎng)了代數(shù)推理能力,并且實實在在地感受到了用“數(shù)”的方法解決函數(shù)問題的優(yōu)越性.

3.3 “代數(shù)推理”與“幾何推理”相互轉(zhuǎn)換

本節(jié)課是搭建抽象概念與具象知識間的橋梁,學(xué)生在深入研究y=ax2+bx+c的圖象與方程ax2+bx+c=0的解后,借助表達(dá)式間的關(guān)系,構(gòu)建了二次函數(shù)和一元二次方程之間的關(guān)系,通過對函數(shù)和對應(yīng)的方程的具體研究形成了對二次函數(shù)和一元二次方程的認(rèn)識．

3.4 “合情推理”與“演繹推理”有機結(jié)合

本節(jié)課,二次函數(shù)與對應(yīng)一元二次方程之間關(guān)系的建立是根據(jù)師生合作,畫出指定函數(shù)圖象,通過觀察、驗證對應(yīng)一元次二方程推斷得出來的,而且把這個經(jīng)驗應(yīng)用到所有的二次函數(shù)中,整個過程符合“合情推理”的特征.而利用二次函數(shù)與一元二次方程的關(guān)系去解決具體問題是一般到特殊的過程,符合“演繹推理”的特征.本節(jié)課“合情推理”與“演繹推理”相互影響.在日常教學(xué)中,要多設(shè)計豐富的數(shù)學(xué)活動,培養(yǎng)學(xué)生的合情推理能力.在例題教學(xué)中,要強化規(guī)范、嚴(yán)謹(jǐn),培養(yǎng)學(xué)生的演繹推理能力.在學(xué)習(xí)新知時,力求發(fā)展這兩種推理能力,這不僅是因為兩種推理方式是相輔相成的,而且有利于學(xué)生完整而嚴(yán)謹(jǐn)?shù)卣J(rèn)識新知.Z