基于離散繞組的磁場式時柵位移傳感器及誤差特性

陳自然， 張桁瀟， 何智穎， 陳鴻友， 余海游

（1. 重慶理工大學 機械檢測技術與裝備教育部工程研究中心，重慶 400054；2. 中煤科工集團重慶研究院有限公司，重慶 400039；3. 時柵傳感及先進檢測技術重慶市重點實驗室，重慶 400054）

1 引 言

精密位移測量技術及器件是高檔數控機床、高端儀器設備等精密高端裝備的核心技術和關鍵功能部件，是實現精密定位與控制的“眼睛”[1-4］，直接決定著系統的性能。光柵采用又精又密的柵線作為測量基準，其加工精度決定測量精度，其密度決定測量分辨力[5-7］。目前，市場上高精度增量式直線光柵的柵距為20 μm，測量精度為±3 μm。為提高測量精度和分辨力，世界領先的德國HEIDENHAIN 公司生產的LIP201 直線光柵[8］的柵距提高到2.048 μm，測量精度達到±1 μm。上海光學精密機械研究所為實現納米級的測量精度，使用超精密激光設備 研 制 了 柵 距 為830 nm 的 光 柵[9］，測 量 精 度 提高到50 nm。光柵的測量精度越高，對柵線刻劃的均勻性和一致性要求越高，制造難度呈幾何指數增長，此類精密光刻技術已逼近極限，很難再進一步提高。同時，光柵使用過程中易受到光電池安裝位置、指示光柵與標尺光柵夾角誤差和衍射光強等因素的影響[10-11］，導致信號質量不穩定，嚴重影響光柵的測量精度。因此，光刻精度和安裝誤差是影響光柵測量精度的兩個重要因素。

針對上述問題，前期課題組提出利用時間提高位移測量精度的方法，發明了時柵位移傳感器[12-17］。本文在此基礎上提出了基于離散繞組的磁場式時柵位移傳感器，通過設計毫米級尺寸的激勵繞組和感應繞組的形狀與排布輸出位移感應信號，實現微米級測量精度，降低了傳感器的制造難度。

2 工作原理

基于離散繞組的磁場式時柵位移傳感器結構主要包含動尺和定尺，動尺和定尺在空間上正對平行安裝，并保持一定的間隔距離δ，如圖1所示。其中，動尺包含基體和正弦形感應繞組陣列，定尺包含基體和激勵繞組陣列。定尺上均勻布置兩行邊長為d的離散矩形激勵繞組，按間隔d等間距排布，其中第一行構成正弦激勵繞組，第二行構成余弦激勵繞組。同行相鄰激勵繞組依次施加相位相差180°的激勵電流信號，如下：

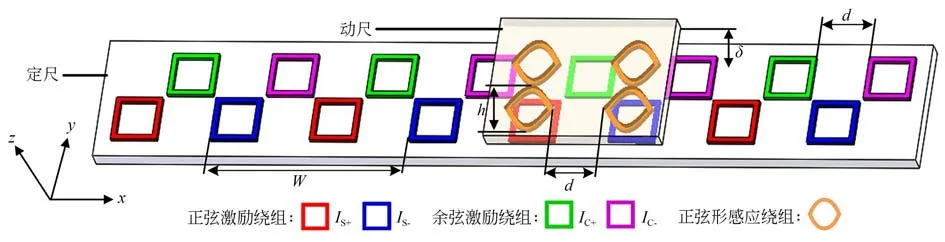
圖1 磁場式時柵位移傳感器總體結構Fig.1 Overall structure of magnetic-field type time-gating displacement sensor

其中：Im為激勵交變電流的最大幅值，ω為激勵交變電流頻率。

動尺包含4 組正弦形感應繞組，記為A，B，C，D，其中正弦形感應繞組A 和正弦形感應繞組B 按相同繞向串聯，正弦形感應繞組C 和正弦形感應繞組D 按相同繞向串聯，如圖2所示。

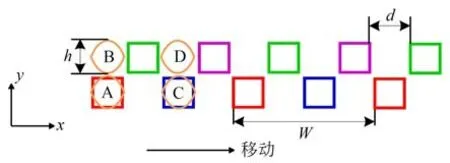
圖2 感應繞組和激勵繞組的位置示意圖Fig.2 Position of induction winding and excitation winding

給定尺上的激勵繞組通入正/余弦激勵電流，當動尺與定尺產生相對位移時，根據電磁感應原理可得正弦形感應繞組A，B 在一個激勵繞組周期極距W內的感應電動勢，即：

其中：k為比例系數，h為正弦形感應繞組的高度，W為極距，x為動尺的運動位移。

同理，正弦形感應繞組C，D 在一個激勵繞組周期極距W內的感應電動勢為：

由疊加定理可得正弦形感應繞組A、B 串聯后的感應電動勢以及正弦形感應繞組C、D 串聯后的感應電動勢，如下：

其中：K=

正弦形感應繞組A 和正弦形感應繞組C 構成差動傳感結構，正弦形感應繞組B 和正弦形感應繞組D 構成差動傳感結構，可有效消除共模信號干擾。因此，正弦形感應繞組A，C 與正弦形感應繞組B，D 串聯后的疊加信號為：

式（5）即為傳感器輸出的攜帶位移信息的行波信號，行波信號的相位變化反映動尺的運動狀態，并隨運動位移發生周期變化，與同頻參考信號比相獲得時間量Δt，進而獲得測量位移量Δx，位移解算方案如圖3 所示。在動尺運動過程中，感應繞組產生輸出的感應信號Ux，經過濾波電路、放大電路的預處理后，由整形電路整形成方波信號，之后輸入FPGA 模塊與同頻參考信號Uf進行比相，由高頻時鐘脈沖插補計數求出相位差的時間量Δt，由此求得運動方向的位移量為：

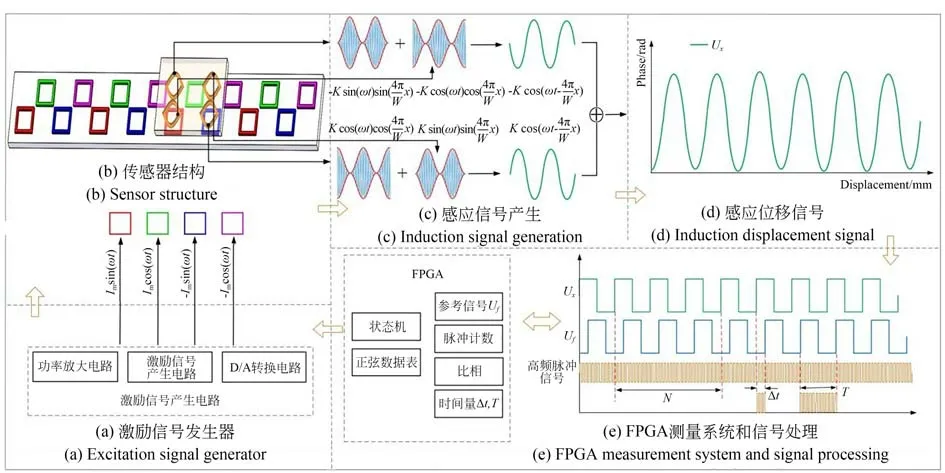
圖3 位移解算方案示意圖Fig.3 Schematic diagram of displacement solution scheme

其中：N為動尺在運動方向上運動的完整對極數，T為參考信號的時鐘周期。

傳感器的測量分辨力可以表示為：

其中：L為量程，N為對極數，fe為激勵信號頻率，fr為用于插補相位差的高頻時鐘頻率。

3 傳感器誤差分析

3.1 駐波信號幅值不等的誤差分析

根據式（5）可知，被測位移主要體現為行波信號的相位變化，因此行波信號質量會直接影響傳感器的測量精度。但加工誤差與人為因素在測量過程中會導致測量誤差，根據基于離散繞組的磁場式時柵位移傳感器的結構和工作原理，這里對兩路駐波信號的幅值不等、相位非正交造成行波信號發生的變化展開討論。

磁場式時柵位移傳感器在測量過程中，由于激勵信號誤差和安裝誤差的影響，合成行波信號的兩路駐波信號幅值不等，使行波信號的相位與理論相位之間存在偏差。以正弦形感應繞組A，B 為例，當感應繞組輸出的信號幅值不等時，式（2）改寫為：

其中：KA，KB分別為正弦形感應繞組A，B 輸出駐波信號的幅值。

三角函數輔助角公式如下：

根據式（9）對兩路駐波信號進行疊加，得到的行波信號如下：

根據式（9）對式（4）進行變形，得到：

將式（10）與式（11）的相位作差可得到由兩路駐波信號幅值不等造成的誤差，即：

反三角函數的表達式如下：

根據式（13）對誤差表達式進行簡化，得到：

由上述分析可知，當合成行波信號的兩路駐波信號的幅值不等時，測量結果會引入2 次諧波誤差。

3.2 駐波信號相位非正交分析

兩路駐波信號在空間上的相位非正交，使得行波信號中引入誤差，主要因為傳感器產生了安裝誤差。此刻設正弦形感應繞組A，B 輸出的駐波信號的幅值相等、初相位不相等，則表達式為：

其中φ為兩路駐波信號空間上的相位差值。

根據疊加定理，兩路駐波信號疊加產生的行波信號為：

根據式（11）和式（12）可得由兩路駐波信號空間相位非正交造成的誤差公式，即：

由式（17）可知，當兩路空間相位非正交的駐波信號合成行波信號時，誤差主要含有0 次諧波（直流分量）和2 次諧波。

4 仿真與誤差分析

為研究激勵信號誤差和動尺的安裝誤差對傳感器輸出的行波信號的影響，使用Maxwell 電磁仿真軟件進行有限元仿真。激勵信號誤差為激勵信號幅值不相同，動尺的安裝誤差一般分為3 種情況：動尺相對于定尺沿X軸、Y軸和Z軸發生了旋轉（分別稱為俯仰、翻轉和偏擺），如圖4 所示。傳感器的基本仿真參數設置如下：運動方向極距W為24 mm，激勵繞組的高度和寬度均為5.8 mm，直徑為0.2 mm，感應繞組高度和寬度均為6 mm，直徑為0.3 mm，感應繞組阻抗為1 MΩ，感應繞組和激勵繞組的氣隙高度為0.6 mm。

圖4 傳感器動尺的不同安裝姿態Fig.4 Different installation attitudes of sensor moving ruler

4.1 激勵信號幅值不相同仿真

仿真中傳感器的動尺移動24 mm，感應信號剛好變化一個完整的周期。在正弦激勵繞組和余弦激勵繞組中通入設定好幅值的激勵信號，得到在兩路激勵信號幅值不同的情況下仿真輸出的行波信號，如圖5 所示。

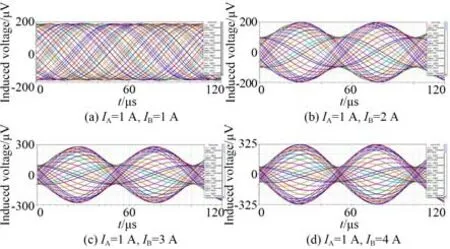
圖5 對極內不同激勵信號幅值下的仿真結果Fig.5 Simulation results under different excitation signal amplitudes within a pitch

計算圖5（a）～5（d）每條正弦曲線的初相位角，并與理論的初相位角相減，得到各空間位置的初相位誤差，最后轉換為對應的誤差曲線，如圖6（a）所示，采用傅里葉變換分析誤差曲線，結果如圖6（b）所示。

由圖6 可知：當兩路激勵信號的幅值為1 A和1 A，位移誤差的峰峰值為18.96 μm；當幅值為1 A 和2 A，位移誤差的峰峰值為25.21 μm；當幅值為1 A 和3 A，位移誤差的峰峰值為39.77 μm；當幅值為1 A 和4 A，位移誤差的峰峰值為48.58 μm。不同激勵信號幅值對應的位移誤差主要包含直流分量和2 次諧波，當兩路激勵信號的幅值差距逐漸變大，直流分量和2 次諧波的幅值明顯增大。

4.2 沿X 軸俯仰姿態的仿真

動尺相對于定尺繞X軸有一個俯仰角度α，如圖7 所示。在仿真模型中，俯仰角度α分別設置為0°，1°，2°和3°，得到不同俯仰角度下仿真輸出的行波信號，如圖8 所示。

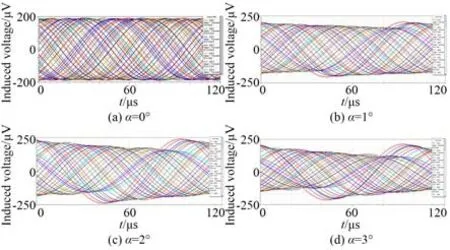
圖8 對極內不同俯仰角度下的仿真結果Fig.8 Simulation results under different tilt angles within a pitch

計算圖8（a）～8（d）中行波信號的初相位和理論初相位的誤差，得到不同俯仰角度的誤差曲線，如圖9（a）所示，采用傅里葉變換分析誤差曲線，結果如圖9（b）所示。

由圖9 可知：α為0°時，位移誤差的峰峰值為18.96 μm；當α為1°時，位 移 誤 差 的 峰 峰 值 為22.11 μm；當α為2°時，位 移 誤 差 的 峰 峰 值 為41.08 μm；當α為3°時，位 移 誤 差 的 峰 峰 值 為41.91 μm。不同俯仰角度下對應的位移誤差主要包含直流分量和4 次諧波，在α從0°增大到1°的過程中，直流分量和4 次諧波的幅值減小，而在α從1°增大到3°的過程中，直流分量和4 次諧波的幅值逐漸增大。

4.3 沿Y 軸翻轉姿態的仿真

動尺相對于定尺繞Y軸有一個翻轉角度β，如圖10 所示。在仿真模型中，偏轉角度β分別設置為0°，1°，2°和3°，得到不同翻轉角度下仿真輸出的行波信號，如圖11 所示。

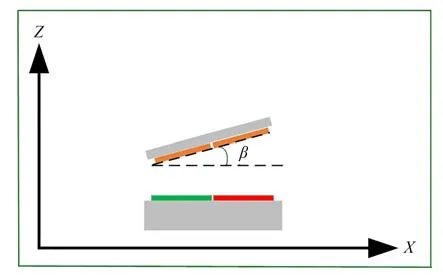
圖10 動尺的翻轉示意圖Fig.10 Flipping diagram of moving ruler

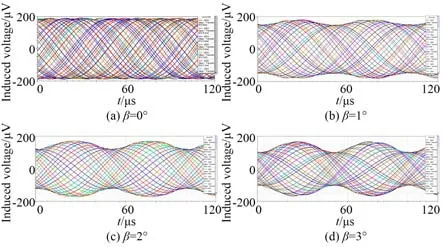
圖11 對極內不同翻轉角度下的仿真結果Fig.11 Simulation results under different flip angles within a pitch

計算圖11（a）～11（d）中行波信號的初相角和理論初相角的誤差，得到不同翻轉角度下的誤差曲線，如圖12（a）所示，采用傅里葉變換分析誤差曲線，結果如圖12（b）所示。

圖12 對極內不同翻轉角度的位移誤差曲線和誤差頻譜Fig.12 Displacement error curves and error spectra for different flip angles within a pitch

由圖12 可知：當β為0°時，位移誤差的峰峰值為18.96 μm；當β為1°時，位移誤差的峰峰值為20.58 μm；當β為2°時，位移誤差的峰峰值為32.95 μm；當β為3°時，位 移 誤 差 的 峰 峰 值 為49.26 μm。不同翻轉角度下對應的位移誤差主要包含直流分量和2 次諧波，并隨翻轉角度的增大，直流分量和2 次諧波的幅值也逐漸增大。

4.4 沿Z 軸偏擺姿態的仿真

動尺相對于定尺繞Z軸有一個偏擺角度θ，如圖13 所示。在仿真模型中，設置偏擺角度θ分別為0°，1°，2°和3°，得到不同偏擺角度下仿真輸出的行波信號，如圖14 所示。

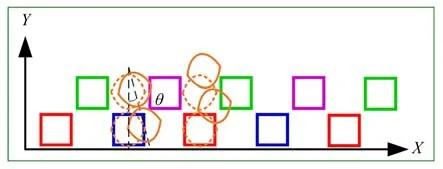
圖13 動尺的偏擺示意圖Fig.13 Deflection of moving ruler

圖14 對極內不同偏擺角度下的仿真結果Fig.14 Simulation results under different deflection angles within a pitch

計算圖14（a）～14（d）中行波信號的初相角和理論初相角的誤差，得到不同偏擺角度下的誤差曲線，如圖15（a）所示，采用傅里葉變換分析誤差曲線，結果如圖15（b）所示。

圖15 對極內不同偏擺角度的位移誤差曲線和誤差頻譜Fig.15 Displacement error curves and error spectra for different deflection angles within a pitch

由圖15 可知：當θ為0°時，位移誤差的峰峰值為18.96 μm；當θ為1°時，位移誤差的峰峰值為27.11 μm；當θ為2°時，位移誤差的峰峰值為32.07 μm；當θ為3°，位 移 誤 差 的 峰 峰 值 為50.3 μm。不同偏擺角度下對應的位移誤差主要包含2 次諧波，且隨著偏擺角度的增大，2 次諧波的幅值也逐漸增大。

綜上所述，仿真結果與理論推導基本相同，兩路激勵信號的幅值不相同、動尺沿X軸俯仰姿態、沿Y軸翻轉姿態和沿Z軸偏擺姿態在測量精度中主要引入直流分量誤差和2 次諧波誤差。經分析，動尺沿Z軸偏擺姿態誤差對測量精度的影響最大，沿Y軸翻轉姿態誤差影響次之，沿X軸俯仰姿態對測量精度的影響最小。

5 實 驗

采用工藝成熟、價格相對低的印制電路板技術制作傳感器樣機，如圖16 所示。激勵繞組在空間上間隔1/4 極距等間隔、均勻排布。激勵繞組分別通入頻率為10 kHz的正/余弦激勵信號，通入同相的激勵信號的激勵繞組按相反繞向串聯。

采用美國AEROTECH 公司制造的直線電機模組PRO190LM-0500-T1-E3-MS1F-PL2-TAS，配置高性能驅動器BLMC-192-A，搭建如圖17 所示的實驗平臺，整個系統的重復精度為±0.5 μm，系統的整體定位精度為±1 μm，分辨率為10 nm。

圖17 時柵位移傳感器誤差特性實驗平臺Fig.17 Experimental platform for error characteristics of time-gate displacement sensor

實驗中，動尺與定尺分別固定在導磁基體上，氣隙高度為0.6 mm，由直線電機帶動傳感器的動尺沿導軌做直線運動。在運動過程中，傳感器動尺的感應繞組通過與定尺產生的空間磁場耦合，感應得到直線電機運動平臺的位移信號。感應信號在放大、濾波并整形成方波信號后，與FPGA 內部的參考信號進行比相，通過高頻時鐘脈沖進行計數得到位移測量值。實驗采用Renishaw 激光干涉儀XL-80 作為測量基準標定傳感器的測量精度，得到傳感器的位移測量誤差，整個實驗平臺結構如圖18所示。

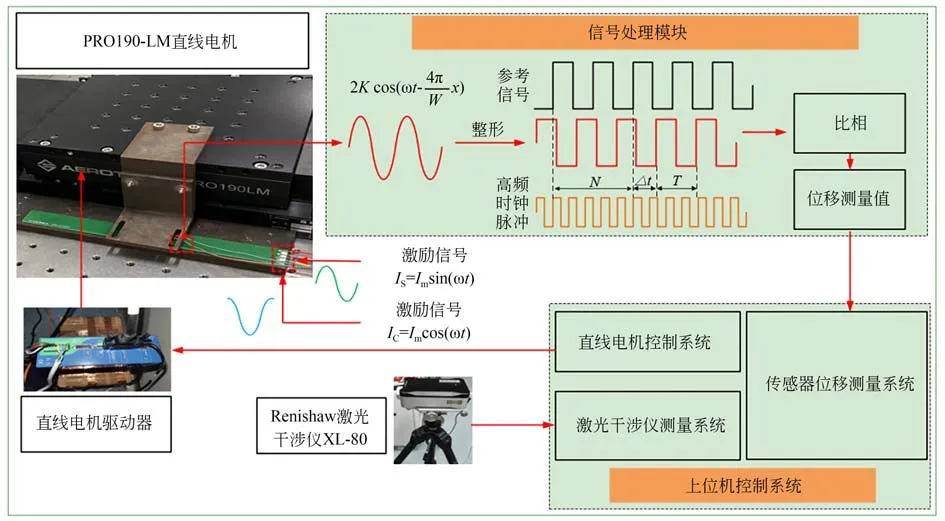
圖18 時柵位移傳感器樣機Fig.18 Prototype of time-gate displacement sensor

圖18 為傳感器樣機，直線電機帶動動尺勻速運動24 mm，即1 個對極，每運動1 mm 信號處理電路的FPGA 芯片同步采集激光干涉儀數據和傳感器運動位移數據。傳感器安裝較為理想，通過設置兩路激勵信號的幅值不同，進行對極內精度實驗，獲得如圖19（a）和19（b）所示的對極內不同激勵信號幅值的測量誤差曲線和誤差頻譜。

然后，在兩路激勵信號的幅值為1 A 和1 A的條件下，對動尺在不同軸上發生安裝偏差產生的測量誤差進行實驗。動尺沿X軸的俯仰角度α分別為0°，1°，2°和3°時得到的測量誤差曲線如圖20（a）所示，采用傅里葉變換進行分析，得到如圖20（b）所示的誤差頻譜。

圖20 對極內不同俯仰角度的測量誤差曲線和誤差頻譜Fig.20 Measurement error curves and errors spectra for different tilt angles within a pitch

重新安裝動尺，沿Y軸的翻轉角度β分別為0°，1°，2°和3°時所得到的測量誤差曲線如圖21（a）所示，采用傅里葉變換進行分析，得到如圖21（b）所示的誤差頻譜。

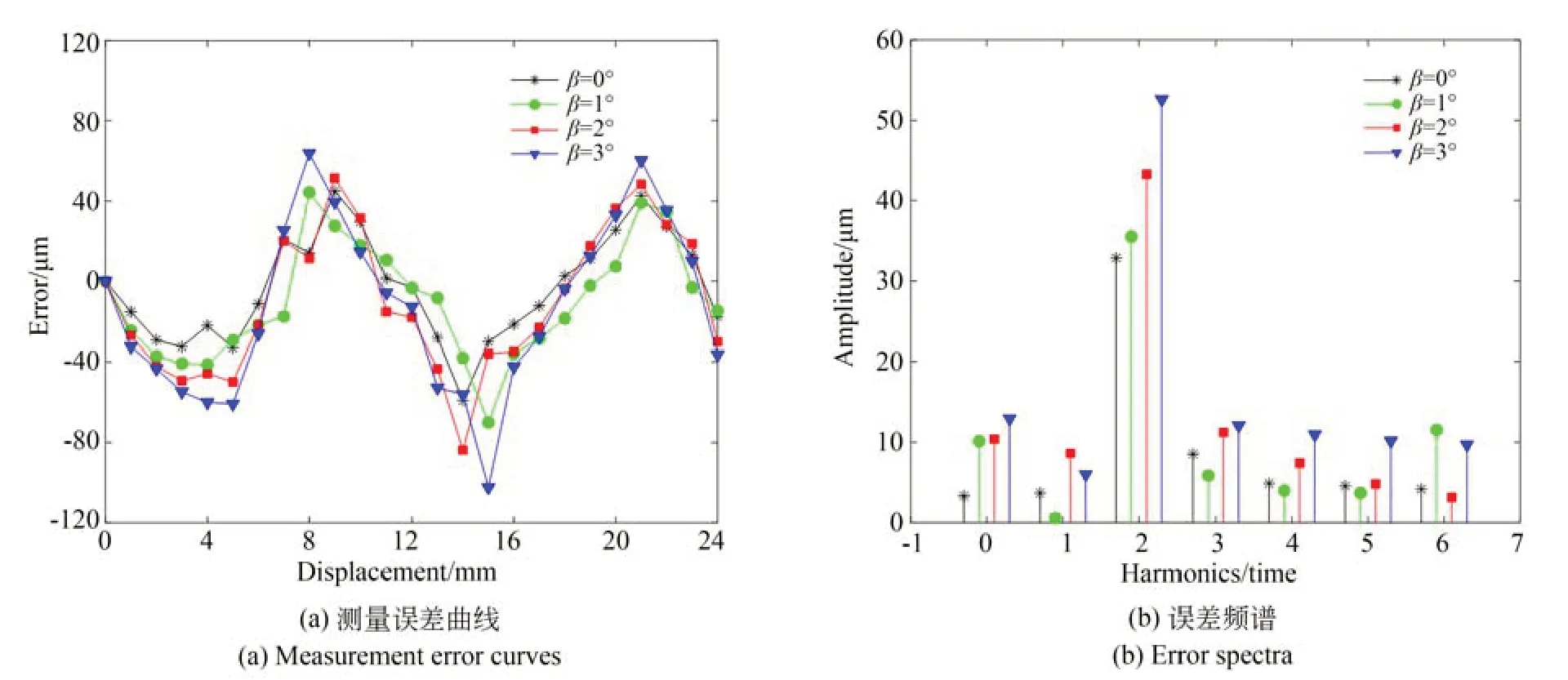
圖21 對極內不同翻轉角度的測量誤差曲線和誤差頻譜Fig.21 Measurement error curves and error spectra for different flip angles within a pitch

再次安裝動尺，沿Z軸的偏擺角度θ為0°，1°，2°和3°時得到的測量誤差曲線如圖22（a）所示，進行傅里葉變換得到如圖22（b）所示的誤差頻譜。

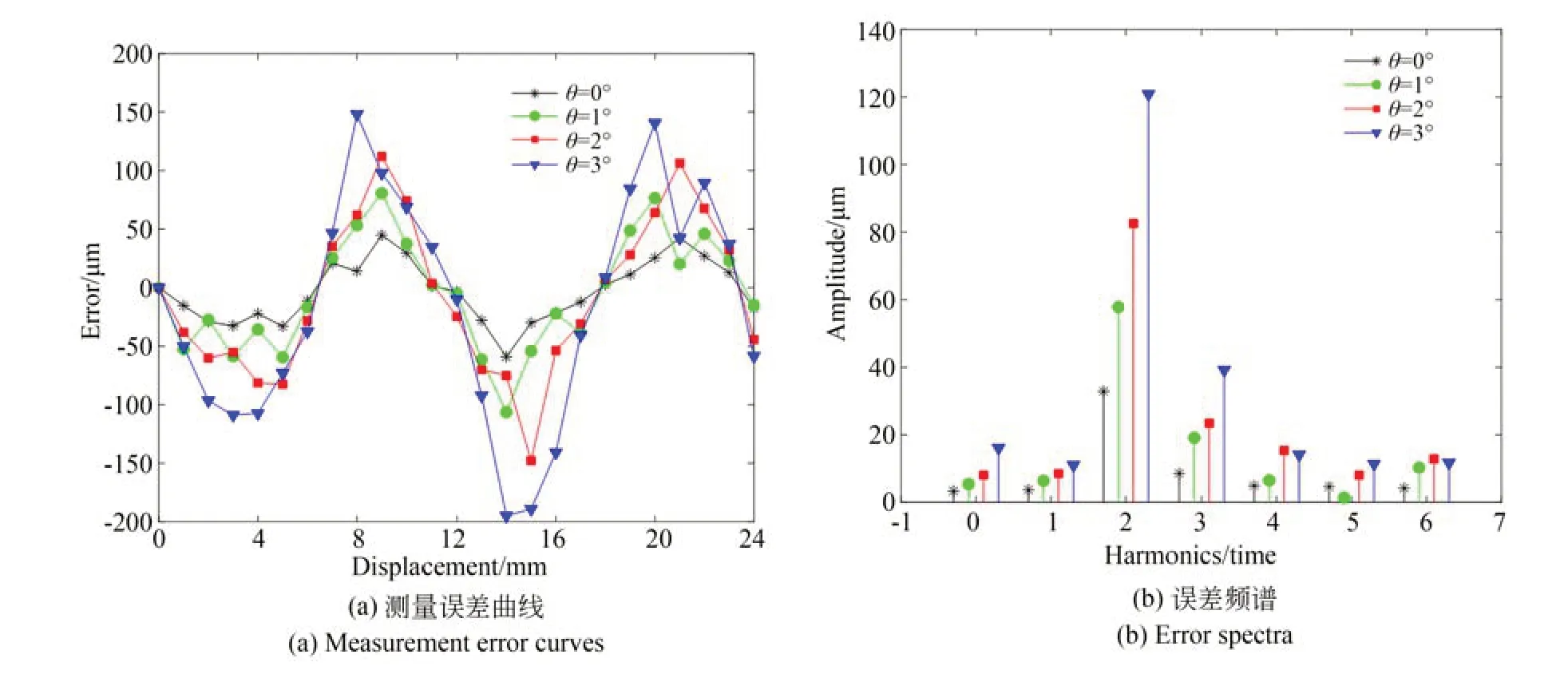
圖22 對極內不同偏擺角度的測量誤差曲線和誤差頻譜Fig.22 Measurement error curves and error spectra for different deflection angles within a pitch

整理實驗數據可知：（1）對極內不同激勵信號幅值為1 A 和1 A，1 A 和2 A，1 A 和3 A，1 A和4 A 時，測量誤差的峰峰值分別為103.95，168.23，231.31 和274.22 μm。當激勵信號相同時，測量誤差中包含的主要誤差成分為2 次諧波；當激勵信號不同時，測量誤差中包含的主要誤差成分為直流分量和2 次諧波，且隨兩路激勵信號的幅值之差越大，直流分量和2 次諧波的幅值也越大。

（2）動尺的俯仰角度α為0°，1°，2°和3°時，測量誤差的峰峰值分別為103.95，104.63，124.72，149.67 μm。當俯仰角度α為0°時，測量誤差的主要成分為2 次諧波；當俯仰角度從1°開始增大時，測量誤差的主要成分為直流分量和2 次諧波，且隨俯仰角度的增大，直流分量和2 次諧波的幅值也增大。

（3）動尺的翻轉角度β為0°，1°，2°和3°時，測量誤差的峰峰值分別為103.95，114.32，135.12，166.29 μm。不同翻轉角度下測量誤差的主要成分相同，為2 次諧波，且隨偏轉角度的增大，2 次諧波的幅值也增大。

（4）動尺的偏擺角度θ為0°，1°，2°和3°時，測量誤差的峰峰值分別為103.95，187.07，259.82，342.97 μm。不同偏擺角度下測量誤差的主要成分相同，為2 次諧波，且隨偏擺角度的增大，2 次諧波的幅值也增大。

在整量程144 mm 內，傳感器安裝較為理想、激勵信號幅值為1 A 和1 A，得到的原始測量誤差曲線如圖23 所示，測量誤差為-59.1～44.85 μm，測量誤差的峰峰值為103.95 μm。采用諧波修正法[18］對原始測量誤差進行修正，修正后測量誤差為-2.85～1.65 μm，測量誤差的峰峰值為4.5 μm。表1 為激勵信號誤差和安裝誤差對整量程內測量精度的影響。

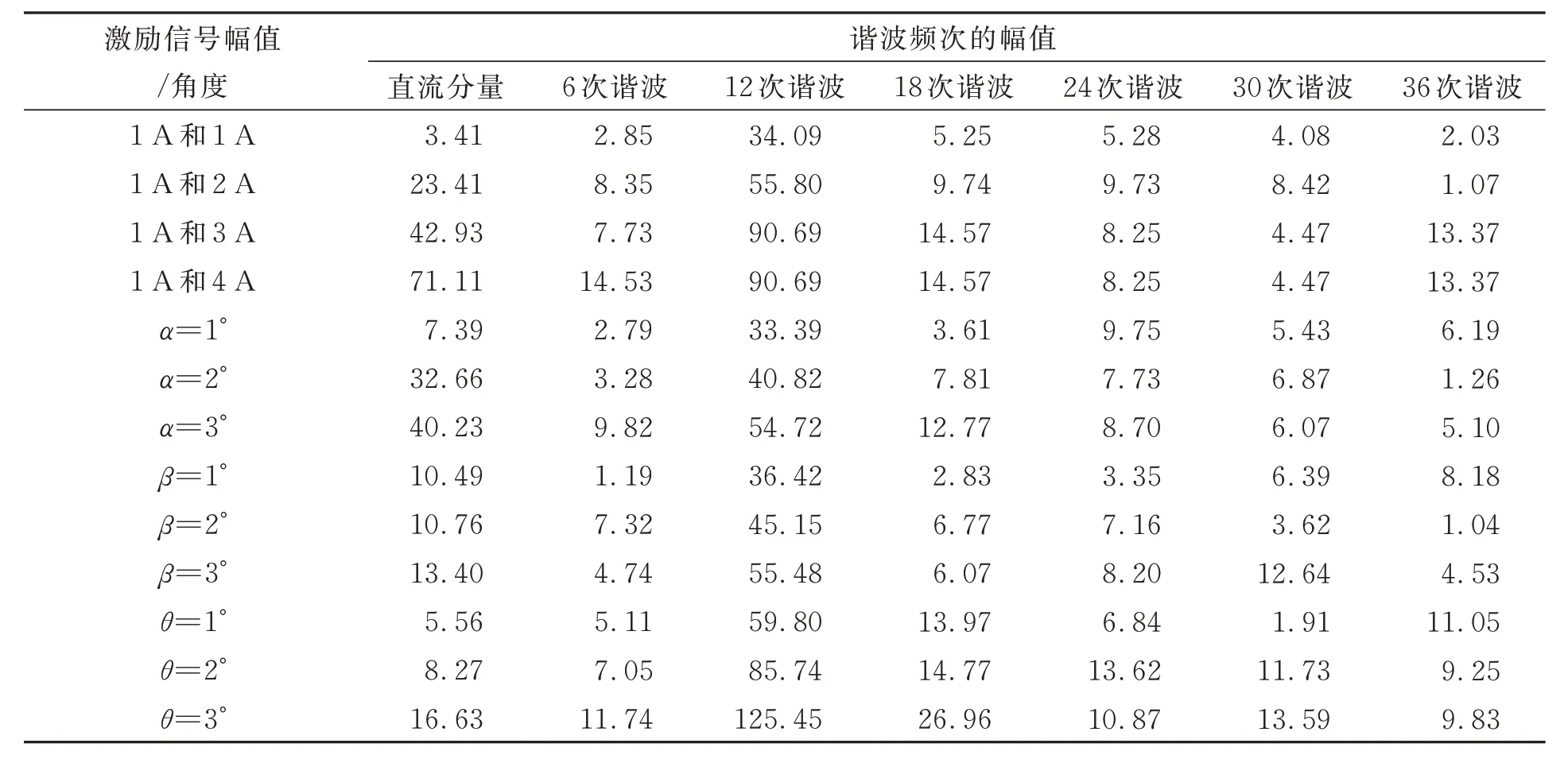
表1 激勵信號誤差和安裝誤差對整量程內測量精度的影響Tab.1 Influence of excitation signal error and mounting error on measurement accuracy over entire scale （μm）

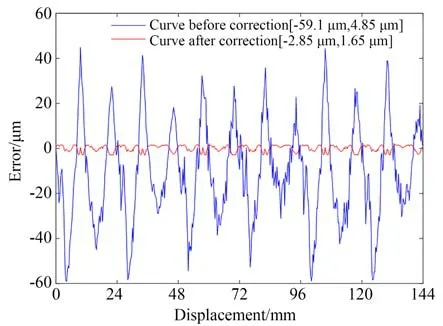
圖23 整量程內諧波修正前后的測量誤差曲線Fig.23 Measurement error curves before and after harmonic correction within full-range

由于傳感器的量程L為144 mm，激勵繞組和感應繞組的對極數為6，激勵信號頻率為10 kHz，FPGA 中進行插補的高頻時鐘脈沖頻率為1.6 GHz，由式（7）計算得到該傳感器的測量分辨力理論上可以達到0.15 μm。

6 結 論

針對高精度位移傳感器難以加工的難題，本文利用組合測量原理，通過設計毫米級激勵繞組和感應繞組的排布方式與形狀實現微米級測量精度，研制了一種基于離散繞組的磁場式時柵位移傳感器。對磁場式時柵位移傳感器在激勵信號幅值不等和動尺沿X軸俯仰姿態、Y軸翻轉姿態和Z軸偏擺姿態下的誤差特性進行了仿真和實驗驗證。仿真與實驗結果表明：在對極內，兩路激勵信號幅值不等和動尺沿X軸俯仰姿態對測量誤差中的直流分量和2 次諧波分量的影響較大，對其他頻次諧波的影響較小；而動尺沿Y軸翻轉姿態和沿Z軸偏擺姿態對測量誤差中的2 次諧波分量的影響較大，對其他頻次諧波的影響較小。因此，激勵信號誤差和安裝誤差在測量精度中引入直流分量誤差和2 次諧波誤差，其中2 次諧波誤差為主要誤差成分，仿真結果與實驗結果基本相同。

在對極內和整量程中，兩路激勵信號幅值不等和不同的安裝誤差對測量精度均有較大影響。安裝誤差中，動尺沿Z軸偏擺姿態對測量精度的影響最大，動尺沿Y軸翻轉姿態對測量精度的影響次之，動尺沿X 軸俯仰姿態對測量精度的影響最小。因此，在基于離散繞組的磁場式時柵位移傳感器的安裝過程中，應著重避免動尺沿Y軸發生翻轉和動尺沿Z軸發生偏擺，確保兩路激勵信號的幅值相同，以保證傳感器的測量精度。

最后進行整量程精度實驗，在144 mm 量程內，傳感器原始誤差的峰峰值為103.95 μm，經諧波修正后測量誤差的峰峰值為4.5 μm，傳感器的分辨力為0.15 μm。綜上表明，通過毫米級尺寸的激勵和感應繞組實現微米級測量精度，可顯著降低傳感器的制造難度，具有重要的工程應用價值。