垂軌環掃衛星影像有理函數模型的構建及精度評估

劉 憲， 薛 武， 王 鵬

（航天工程大學，北京 101416）

1 引 言

有 理 函 數 模 型（Rational Function Model，RFM）最初作為IKONOS 影像的成像模型由Space Imaging 公司推出，因其精度高、適用性強、保密性好等特點而得到廣泛應用[1］。很多學者對衛星影像RFM 精度進行了研究，Naga-subramanian 等使用IRS-P6 LISS-4 長條帶多光譜影像構造RFM 與嚴格成像模型進行精度對比，實驗表明二者的擬合誤差小于1 像素[2］；蔣永華等對珠海一號衛星補償鏡頭畸變參數后，影像RFM 的絕對精度優于0.5 像素[3］；唐新明等對資源三號衛星經傳感器校正后的影像產品進行RFM 構建實驗，其前視、后視、正視影像RFM 與嚴格成像模型的擬合誤差均優于0.001 像素[4］；張力等對SPOT-5 不同傳感器獲取的全色與多光譜影像構建RFM，RFM 與嚴格成像模型的擬合誤差不大于0.05 像 素[5］。大量研究表明，對現有衛星而言，RFM 能夠在一定程度上代替嚴格成像模型，滿足測繪生產需求。

隨著衛星技術的進步與發展，線陣垂軌環掃成像構思被提出[6］。區別于當前光學遙感衛星主要使用的三線陣、雙線陣或單線陣/面陣成像體制[7］，垂軌環掃成像的線陣CCD 傳感器沿衛星飛行方向安置，在衛星飛行過程中傳感器繞衛星縱軸360°旋轉掃描，視場在垂直軌道方向上不斷疊加以實現環掃成像。在軌道高度500 km、焦距3 500 mm 的情況下，垂軌環掃傳感器能實現星下點空間分辨率1 m、影像東西跨度3 000 km 的成像指標，兼顧高空間分辨率與大范圍地物覆蓋。作為一種新型成像體制，垂軌環掃成像對一些應用于衛星的成熟理論提出了挑戰。

目前，在垂軌環掃成像研究中，鐘靈毓構建了嚴格成像模型并對模型的正確性進行了驗證[8］，薛武系統分析了垂軌環掃傳感器幾何處理的難點，提出了初步解決方案[9］，而后提出一種以匹配同名點作為約束條件的幾何糾正方法[10］，但目前尚無RFM 的相關研究。本文以生成的模擬影像及姿軌數據為基礎，使用地形相關、地形無關方案構建不同幅寬影像RFM，探究不同幅寬影像在不同控制點獲得方案與物方坐標系下的RFM 擬合精度。

2 嚴格成像模型與有理函數模型的構建

2.1 成像原理

垂軌環掃成像將多條線陣CCD 拼接成一條長線陣CCD，沿衛星飛行方向安置，在衛星飛行過程中傳感器光軸繞衛星縱軸旋轉360°，在傳感器旋轉至一定角度范圍時進行掃描成像，視場在掃描方向不斷疊加[10］，實現大視場寬幅成像。垂軌環掃成像與線陣推掃成像的對比如圖1 所示。

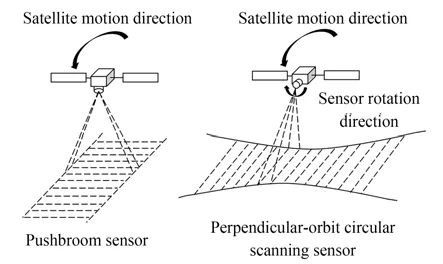
圖1 線陣垂軌環掃成像與推掃成像對比Fig.1 Comparison of perpendicular-orbit circular scanning sensor with pushbroom sensor imaging mode

為滿足立體測繪、三維重建等需求，衛星可搭載雙相機獲取立體像對。兩臺相機“背靠背”反向安置，下視相機主光軸垂直軌道向下，前視相機主光軸沿軌向前傾斜一定角度，在環掃過程中雙相機交替成像，獲取立體影像。圖2 為雙相機成像示意圖，其中藍色、黃色分別為下視與前視相機成像視場（彩圖見期刊電子版）。

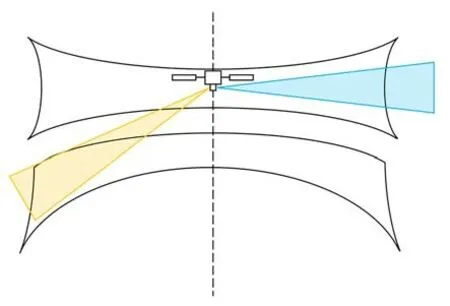
圖2 雙相機成像示意圖Fig.2 Schematic diagram of dual-camera imaging

2.2 像方坐標系定義

垂軌環掃獨特的成像方式使得部分像方坐標系在定義與使用上與推掃式傳感器有所區別。對于瞬時影像坐標系，在推掃成像下，以影像每條掃描行主點為原點，沿掃描線方向為y軸，沿衛星運動方向為x軸[11］；在垂軌環掃成像下，以影像每條掃描行主點為原點，掃描線方向為x軸，傳感器環掃方向為y軸。對于該定義下的瞬時影像坐標系坐標，推掃成像中x值恒等于0，而垂軌環掃成像中y值恒等于0。兩種瞬時影像坐標系如圖3 所示。對于傳感器坐標系，推掃成像與垂軌環掃成像定義下的坐標原點均位于掃描行投影中心，x，y軸定義同瞬時影像坐標系，z軸由右手法則確定。

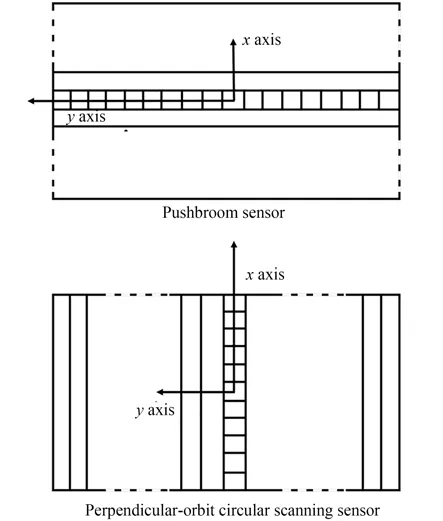
圖3 垂軌環掃與線陣推掃的瞬時影像坐標系對比Fig.3 Comparison of instantaneous image coordinate system between vertical orbit ring scanning sensor and pushbroom sensor

2.3 嚴格成像模型構建

WGS84 坐標系下，記地面點坐標為[X，Y，Z]T，衛 星GNSS 天 線 相 位 中 心 坐 標 為[XGNSS，YGNSS，ZGNSS]T，則 物 方 矢 量 為[XXGNSS，Y-YGNSS，Z-ZGNSS]T，將 它 轉 換 至 衛 星本體坐標系：

其中：[x，y，-f]T為物方矢量在傳感器坐標下的坐標，Rcambody表示衛星本體坐標系到傳感器坐標系的轉換矩陣。共線條件方程實質是投影中心、像點、物點三點共線，即像方矢量與物方矢量共線，綜合式（1）有：

其中λ為比例系數。考慮到GNSS 偏移矢量和投影中心偏移矢量的數值較小且一定程度上相互抵消[12］，式（3）可簡化為：

2.4 有理函數模型構建

RFM 的表達式為[13-14］：

其 中：(rn，cn)，(Xn，Yn，Zn)分 別 為 第n個 控 制 點歸一化后的像方、物方坐標；pi(i=1，2，3，4)為物方坐標構成的多項式，多項式中各項冪次不超過3，具體形式為：

其中ai為多項式系數。將式（5）線性化后，采用嶺估計法求解有理函數模型參數（Rational Polynomial Coefficients， RPC）。

RPC 的解算需要地面控制點（Ground Control Point， GCP）的像方坐標與物方坐標，根據坐標的獲取方式可分為地形相關與地形無關兩種方案。地形無關方案使用嚴格成像模型計算得到覆蓋影像物方范圍的空間格網點坐標[13，15］；地形相關方案通常為實地測量、地圖選點[11，14］或匹配同名點[16］的方式得到控制點坐標。其解算的RPC 精度與控制點的數量、分布和精度密切相關[14］。由于垂軌環掃衛星影像范圍遠超傳統衛星影像且原始影像存在較大畸變，人工選取一定數量、分布較為均勻的控制點耗時耗力；匹配同名點又難以保證其精度與空間分布。因此，本文的地形相關方案采用在影像范圍內布設物方平面格網，然后由數字高程模型（Digital Elevation Model， DEM）內插得到高程，進而反算至像方得到控制點坐標。此方案的整體思路與地形無關方案[15］類似，但高程值由DEM 內插得到。雖然GCP 生成中使用嚴格成像模型，但由于物方坐標依照地形起伏分布，故稱之為地形相關方案。

地形無關方案的步驟為：

（1）在像方按一定像素間隔布設均勻格網點，得到每個格網點的像素坐標(ri，ci)；

（2）求取影像對應地面范圍的最大、最小高程Hmax，Hmin，并將高程范圍均分為m層；

（3）將格網點像素坐標(ri，ci)和各個高程面的高程Hm帶入共線條件方程，與橢球方程聯立解算物方坐標(Xi，Yi，Zi)，即得到物方空間分布的m層虛擬控制點的像方和物方坐標。

地形相關方案的步驟為：

（1）在影像第一行、最后一行和第一列、最后一列均勻選取若干像點，平均高程帶入共線條件方程和橢球方程聯立求得物方坐標，構成封閉多邊形表示影像對應的大致地面范圍。

（2）在DEM 上布設影像范圍內均勻格網點，由物方平面坐標(Xi，Yi)內插得到高程坐標Zi。

（3）使用反投影計算進行物點最佳掃描行搜索，得到控制點的物方和像方坐標。

2.5 反投影計算分析與改進

由于線陣影像多中心投影的特性，在將坐標由物方換算至像方時，首先需確定物點對應的外方位元素，即確定對應的成像掃描行，此過程稱為反投影計算。該方法用于地形相關方案中得到控制點的像方坐標，依據原理可主要分為基于像方空間特性和基于物方空間特性兩種方式。由于垂軌環掃單景影像變分辨率[9］，影像投影面間不具備平行關系[10］，現有的基于傳感器物方空間特性提出的反投影算法[17-20］較難直接應用于垂軌環掃影像，因此本文采用基于像方空間特性的反投影計算方法——二分法[21-22］進行討論。

不同于推掃成像，垂軌環掃成像時每一掃描行對應影像的一列，因此后續討論基于此種對應關系展開。記地面點P的物方坐標為(X，Y，Z)，像方坐標為(rp，cp)，掃描行列數與其外方位元素分別為cp與eopcp，影像第i個掃描行對應的外方位元素記為eopi。將P(X，Y，Z)與eopi帶入共線條件方程，可算得物點在第i個掃描行中對應的傳感器坐標系下的位置坐標，記其y軸分量為yi。由2.2 節所述像方坐標系定義，P(rp，cp)在第cp列影像對應的瞬時影像坐標系下的像點坐標y軸分量不大于0.5 像素。將其轉換至傳感器坐標系后，相應y軸分量數值上接近0。因此，當共線條件方程中帶入P(X，Y，Z)與eopcp時，得到傳感器坐標系y軸分量ycp近似為0。當共線條件方程中帶入P(X，Y，Z)與eopi(i≠cp)時，近似相當于求解P(rp，cp)在第i個掃描行傳感器坐標系下的坐標，此時yi的絕對值大于ycp。由于各掃描行傳感器坐標系y軸的定義方向相同，當掃描行號i大于cp時，yi雖然數值有所變化，但符號上保持統一，反之亦然。反投影計算原理如圖4 所示。

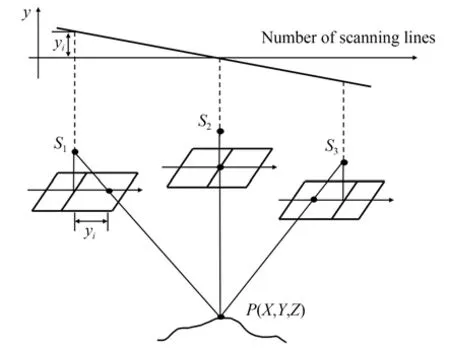
圖4 反投影計算原理Fig.4 Schematic principle for back project calculation

將P(X，Y，Z)與eopi，(i=1，2，…，n)依 次帶入共線條件方程，做出yi值隨列數變化的散點圖像，離散點分布應符合單調單零點曲線走勢，如圖5（a）所示，曲線中近似零點處對應列數即為所求。以掃描行范圍(s，s+1，…，n)作為搜索區間，分別選取eops，eopm，eopn(m=n/2）帶入共線條件方程，將(ys*ym)與(ym*yn)分別作為判別式，若某一判別式小于零，則此區間內包含零點，即最佳掃描行位于此區間內，并按照此區間起止更新掃描行搜索范圍。如此迭代，將搜索區間逐次對半縮減直至區間長度小于給定閾值。而后在區間內逐行計算yi，數值最小者即為所求。此即二分法的實現過程。

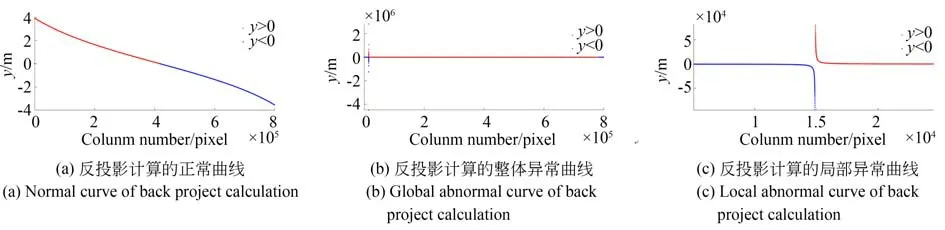
圖5 像方反投影計算曲線Fig.5 Curves of back project calculation

但是嚴格來講，對于多中心投影，共線條件方程只在帶入物點P(X，Y，Z)與對應eopcp時嚴格成立。帶入eopi(i≠cp)時，得到的結果僅能進行符號上的定性判斷，且其可靠程度隨掃描行號i與掃描行號cp間距離的增大而減小。垂軌環掃單景影像的投影中心數量最多超過100萬，當掃描行i與cp各自對應的物點相距過大時，將導致eopi帶入共線條件方程后分母位置數值變化經過零點，從而使所求yi值出現類似無窮間斷點的躍變現象（如圖5（b）和圖5（c）所示），改變零點兩端yi值符號的一致性，使兩個迭代判別式均小于零，從而導致二分法無法判斷物點所在區間。

對二分法迭代判斷規則進行改進。當無法由判別式符號關系判斷物點所在區間時，由影像中心位置的像素坐標及平均高程算得星下點概略坐標（記為Lssp），通過比較物點與星下點經度的坐標關系得到物點所在的初始區間，以此避免因y值躍變導致二分法計算失效。二分法與改進二分法的迭代流程如圖6 所示。圖中，s，m，e分別為搜索區間內第一條、中間條、最后一條掃描行影像列數，初始搜索區間為整景影像列數范圍；ys，ym，ye為上述三列掃描行外方位元素與物點帶入共線條件方程算得的y值。

圖6 反投影計算與改進算法流程Fig.6 Flow chart of back project calculation and improved algorithm

3 實驗及分析

由于目前尚無公開資料顯示有搭載線陣垂軌環掃傳感器的衛星在軌運行，因此本研究使用課題組開發的衛星影像模擬軟件生成模擬影像與姿軌數據開展實驗，軟件界面如圖7 所示。實驗 環 境 為Microsoft Win11 64 位 操 作 系 統，CPU型號Inter（R） i7-12700H 2.70 GHz，內存容量為32 GB，相 關 程 序 基 于MATLAB 2022a 編 寫實現。

圖7 模擬影像仿真軟件界面Fig.7 Interface of simulation image software

3.1 實驗數據準備

實 驗 分 別 以 青 海 省 天 峻 縣（97.7° E，38.7°N）、青海省格爾木市（94°E，36°N）為原始影像的中心位置，生成前視、下視一景完整3 000 km 影像的姿軌數據，通過計算得到不同幅寬下對應掃描行外方位元素用以解算RPC。影像范圍跨度廣、地勢起伏大，包括高原、山地、平原在內等多種地形。前視、下視影像對應的范圍分別如圖8（a）和8（b）所示。

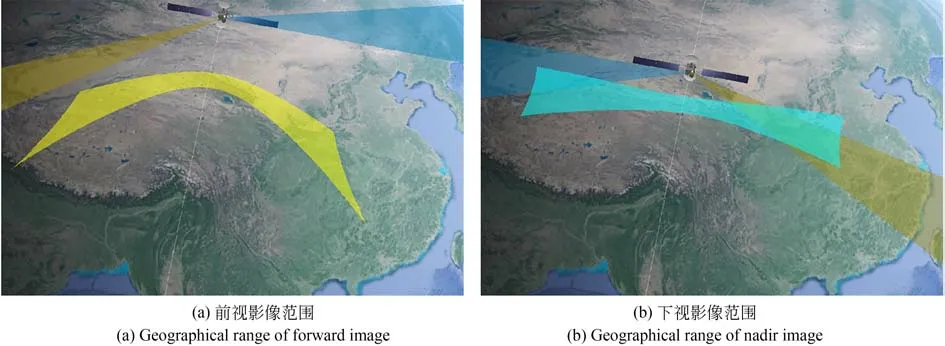
圖8 影像范圍示意圖Fig.8 Schematic diagram of image range

3.2 改進反投影計算驗證

在兩景3 000 km 幅寬影像行列范圍內生成10 萬個隨機像方點(ri，ci)，對每個像點賦予平均高程附近的隨機高程值Zi，由共線條件方程計 算 得 到10 萬 個 虛 擬 物 方 點(Xi，Yi，Zi)。將 虛擬物方點代入改進算法，將計算得到的像點坐標(r'i，c'i)與原始像方坐標(ri，ci)作差得到反投影計算誤差，并標記直接使用二分法時無法計算的點位。計算無效點位（標紅）如圖9 所示（彩圖見期刊電子版），行方向上均勻分布，列方向上分布在影像兩側一定范圍內，分布與2.5 節中所述互為印證。

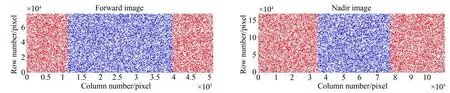
圖9 反投影計算無效點位Fig.9 Invalid points of back project calculation

圖10 表示兩景影像反投影計算的誤差直方統計結果。由圖可見，下視影像行方向誤差呈現零均值正態分布，符合偶然誤差特性[23］；前視影像行方向誤差則存在整體偏移。二者列方向的誤差分布趨勢相同，集中分布在關于0 值近似對稱的兩處位置，呈現出明顯的規律性。圖11 為反投影計算誤差的矢量方向，前視影像誤差矢量整體沿行方向；下視影像誤差矢量指向影像中心，且誤差隨著距影像中心距離的增大而增大。即對于像方反投影計算，造成前視影像誤差的主要因素為傳感器沿軌的安裝角度；造成下視影像誤差的主要因素為掃描行成像時的環掃角度。

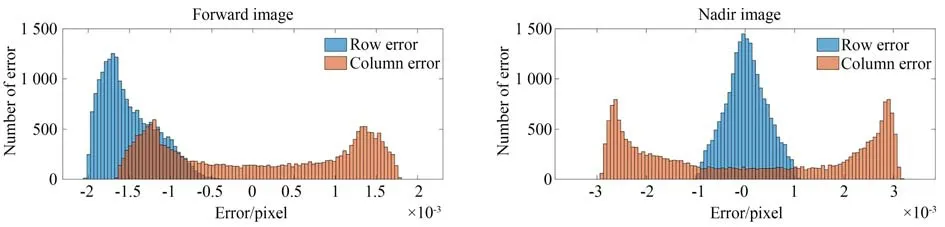
圖10 反投影計算誤差直方統計圖Fig.10 Histogram of back project calculation error

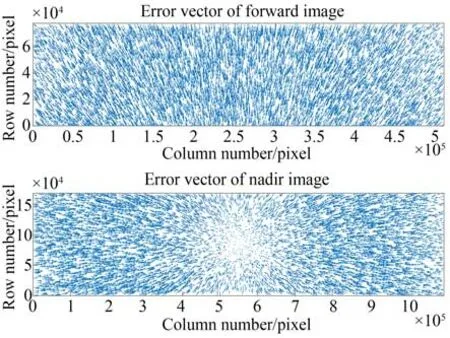
圖11 反投影計算誤差矢量圖Fig.11 Vector diagram of back project calculation error

3.3 有理函數模型精度評價

實 驗 以100 km 跨 度 為 間 隔，采 用2.4 節 所述方案構建不同幅寬RFM。生成雙倍密度的格網點作為檢查點坐標，將其物方坐標帶入RFM中計算得到像方坐標(rRi，cRi)，與原始像方坐標(ri，ci)作 差 并 統 計 其 均 方 根 誤 差（Root Mean Square Error， RMSE），作為擬合能力評價指標。為探究不同物方坐標系對RFM 擬合能力的影響，所有RPC 均在WGS-84 地心直角坐標系與大地坐標系下進行解算。不同條件下得到的RFM 擬合誤差如圖12 所示，圖中GCP 為控制點，CP 為檢查點。圖12（a）和12（b）分別為地形無關、地形相關方案的結果。經對比分析可知，不同方案下RFM 的擬合誤差均隨影像幅寬的增加而增加，但在地心直角坐標系下解算的RPC 精度明顯更優。對于下視影像，在大地坐標系與地心直角坐標系下擬合誤差達到1 像素的 幅 寬 分 別 為300 km，1 100 km；對 于 前 視 影像，達到1 像素誤差的幅寬分別為400 km，1 900 km。雖然地心直角坐標系下解算的RPC 在2 000～3 000 km 幅 寬 內 誤 差 呈 明 顯 增 加 的 趨勢，但其誤差數值遠小于同幅寬大地坐標系下構建的RFM 擬合誤差。

若采用大地坐標系解算垂軌環掃衛星影像RPC，則地球曲率是影響RFM 精度的主要因素。對于定義在大地坐標的控制點(B，L，H)，其實質表示分布在球面上的點，但在計算機求解過程中，大地坐標被認為是一組三維笛卡爾坐標系下定義的直角坐標。即具有相同高程的控制點所表示的曲面被認為是空間平面，使得大地坐標下控制點的物方坐標并不能反映真實的物方空間關系，進而導致誤差較大。

考慮到地球半徑較大（6 371 km），且一般衛星影像幅寬較小（十幾至幾十公里），而RFM 二階項又能夠擬合一定的地球曲率誤差，因此對于傳統衛星影像而言，在大地坐標系仍能夠得到很好的擬合精度。而垂軌環掃衛星影像單景影像的最大幅寬達3 000 km，地球曲率帶來的影響不可忽視。隨著影像幅寬的增加，地球曲率的影響逐漸明顯，導致擬合誤差急劇上升。3 000 km 幅寬影像在大地坐標系下的擬合誤差在132.33～3 004.25 像素，改用地心直角坐標系后，擬合誤差降至7.67～27.50 像素。

本文所用地形相關方案解算得到的RPC 精度優于地形無關方案。RFM 是通過數學表達式構建像方坐標與物方坐標間的投影關系。地形相關方案的格網點嚴格依據地形起伏分布，能夠反映真實的物方空間。地形無關方案的格網點分布則由物方坐標的平面與高程范圍確定，是包含真實物方空間在內的、對物方空間范圍的延伸與拓展，在控制點分布上，可認為地形無關方案覆蓋了地形相關方案。從數學擬合角度考慮，地形無關方案是對物方空間范圍內分布的全部控制點進行全局最優擬合，而地形相關方案只對反映真實地表起伏的部分控制點進行局部最優擬合。在構建像方、物方坐標間擬合關系時，若全局最優解能得到高精度結果，則局部最優解必然也能得到高精度結果；若解算的局部最優解已存在較大的擬合誤差，則考慮全局最優解的結果誤差必然更大。

雖然前視影像RFM 擬合誤差整體小于下視影像，但并不能僅以像素誤差作為對比兩景影像幾何精度的依據。由于傳感器參數不同，下視影像分辨率約為前視影像的2 倍，在單個像元對應地面范圍不同的情況下僅以像素誤差對兩景影像質量進行評價是不可靠的。事實上，下視影像不僅空間分辨率優于前視影像，且由于下視相機主光軸垂直軌道向下，沿軌方向的安裝角度為0°，原始影像上地物畸變的程度也明顯低于前視影像，在未來的測繪生產中，下視影像具有更好的應用潛力。

4 結 論

本文介紹了垂軌環掃傳感器的成像原理，構建了其嚴格成像模型與有理函數模型。在使用地形相關方案構建RFM 的過程中，針對垂軌環掃衛星影像超大幅寬的特點提出一種結合DEM的控制點布設方案；并提出以星下點概略坐標判斷掃描行搜索區間的改進方案，解決了反投影計算失效的問題。在此基礎上開展不同方案、幅寬和坐標下的RFM 構建實驗，實驗結果表明：對基于像方空間關系的反投影計算，本文提出的改進方案能夠有效解決二分法在垂軌環掃衛星影像大幅寬條件下的搜索失效問題，實現3 000 km 幅寬整景影像范圍內任意物方坐標到像方的求解。在大地坐標系與地心直角坐標系下構建的RFM，下視、前視兩景影像的幅寬分別不大于300 km，400 km 與1 100 km，1 900 km 時，擬合誤差小于1 像素。在滿足上述條件時，RFM 能夠近似替代嚴格成像模型；而對于一景3 000 km 幅寬的影像，RPC 難以實現高精度擬合。在大地坐標系下，受地球曲率的影響，大幅寬影像解算的RPC 精 度 極 差（3 000 km 最 小 誤 差 為132.33 像素），采用地心直角坐標系能得到較高的擬合精度（3 000 km 最小誤差為7.67 像素）。對比地形相關與地形無關2 種方案解算的RPC 擬合誤差，影像幅寬較小時，二者精度相當；在大幅寬條件下，前者高于后者。以3 000 km 幅寬影像為例，相較于后者，前者在大地坐標系與地心直角坐標系下解算的兩景影像RPC 的擬合誤差分別降低了35.4%，67.8%與9.2%，12.1%。

后續的工作重點如下：首先，反投影計算是本文所用地形相關方案的基礎，雖然基于像方的反投影計算原理簡單、直觀，但每次迭代求解像點坐標都涉及到十數次共線條件方程運算，計算量大、效率低下，如何利用物方空間關系實現高效率反投影計算有待進一步探究。其次，傳統衛星影像的RPC 精度可達亞像素水平，而垂軌環掃影像僅在部分條件下能夠滿足該精度水平。對于一景3 000 km 影像而言，無論何種方案下解算的RPC 都難以滿足高精度擬合的要求。因此，有必要探究不同的RPC 參數優化方案與誤差補償模型對RFM 擬合精度的提升。最后，雖然RFM在構建時具有物方坐標形式靈活的特點，但目前基于RFM 的各項影像處理與生產工作均在大地坐標系下進行。對于垂軌環掃衛星影像，雖然在地心直角坐標系下能夠獲高精度的RPC，但由于2 種坐標系的定義有本質區別，其能否直接帶入現有技術流程進行處理有待探究。