內斜齒輪磨削加工誤差在線監測與補償*
浮文華 王會良② 蔣 闖②
(①河南科技大學機電工程學院,河南 洛陽 471003;機械裝備先進制造河南省協同創新中心,河南 洛陽 471003)
數控機床是汽車、航空航天和軍事領域中使用最廣泛的制造設備之一[1-2],在工業中起著重要作用,而機床誤差是影響加工精度最主要的原因,影響著行業的整體發展。因此,在保證機床加工效率的基礎上提高其加工精度是目前亟需解決的問題。
機床加工精度一直受國內外學者們的關注,針對機床誤差模型[3-4],分別提出了多體系統理論、矢量法和齊次坐標變換等建模方法。田鳳楨等[5]利用多體系統理論,設計機床加工零件相應運動鏈,并對其加工誤差進行分析;付國強等[6]根據指數積理論和坐標系微分運動理論,建立了運動軸幾何誤差貢獻值模型,提出了運動軸幾何誤差靈敏度分析方法;楊斌[7]利用內置傳感器信息,結合數控機床運動學模型,提出了一種利用內置傳感器測量機床動態加工誤差方法;史燕等[8]采用優化PID 控制器中的關鍵參數,對多軸聯動數控機床運動誤差進行補償,驗證所提方法具有良好的適應性。若要提高機床加工精度就要控制其加工誤差,大多數會將誤差補償技術[9-11]作為提高數控機床精度的主要途徑。
本文對磨削內斜齒輪加工誤差展開研究,利用多體系統和齊次坐標變換原理,建立機床刀具相對于工件的幾何誤差模型,通過加工過程在線監測,進行數據采集和分析,對其進行反向誤差補償。這對提高機床加工精度具有重要作用,對生產精密零件企業的發展具有重要意義[12]。
1 多體系統的機床運動學模型
本文采用多體系統原理[13-14],以數控機床磨削內斜齒輪為例建立其運動學模型,該數控成型砂輪磨齒機擁有X、Y、Z、A、C五個聯動軸。其中,X、Z、C軸是機床磨削系統的主要運動軸,X軸和Z軸與機床床身固定,C軸是工件分度數控回轉臺,安裝在X軸上;Y軸和A軸輔助運動,A軸用來控制砂輪的旋轉,實現內斜齒輪的加工,安裝在Z軸的工作臺上。機床運動軸示意圖如圖1 所示。

圖1 機床運動軸示意圖
1.1 多體系統拓撲結構和低序體陣列
根據對內斜齒輪磨削系統進行運動學分析,把機床系統分為兩個運動鏈,從機床機身開始到工件端結束的是工件運動鏈,從機床機身開始到刀具結束的是刀具運動鏈。兩者確定各運動部件的相鄰低序體關系,通過運動關系對個運動軸進行編號,數控磨齒機機床的拓撲結構圖如圖2 所示。
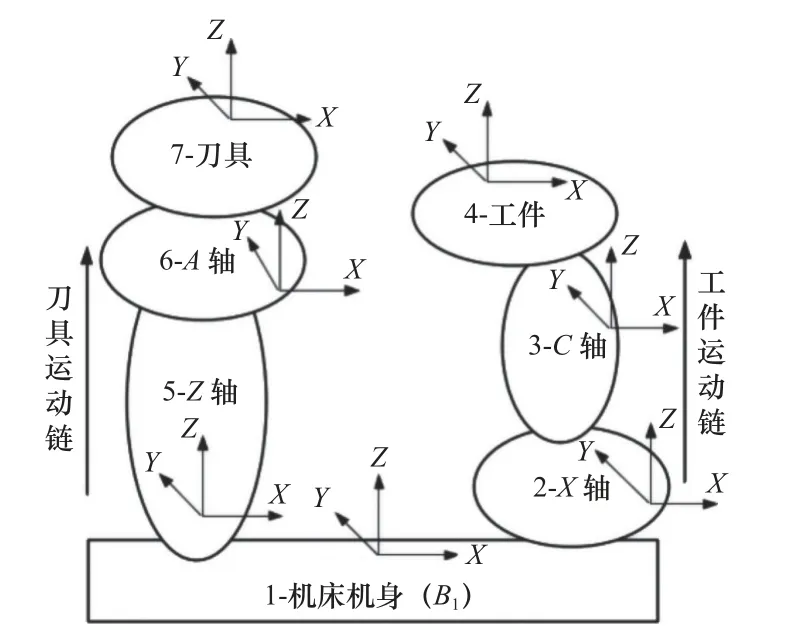
圖2 數控磨齒機拓撲結構圖
由圖2 可知,在該多體系統中,只有B1運動體是最開始標記的,其他每個運動體都有相鄰的序號運動體,通過對該系統當中的各個運動體進行序號列表,用L(K)來表示,K為運動體在系統的序號。
假設S是K的相鄰低序體,用公式可以表達出相鄰運動體的關系:
低序體算子用L表示,則有:
低序體算子的定義為
通過上述公式可得出多體系統的低序體陣列,見表1。

表1 多體系統的低序體陣列
1.2 加工誤差幾何模型
內斜齒輪磨削系統在圖2 所示工件到刀具運動鏈排序為:從工件連接C軸連接X軸至機身,再從機身連接Z軸連接A軸至刀具結束。因此內斜齒輪磨削系統運動鏈中的各個運動體坐標系之間的理想狀態坐標變換關系矩陣如下:TgC、TCX、TXJ、TJZ、TZA、TAW。
由表2 的坐標變換矩陣,可以得到磨削內斜齒輪多體系統在理想狀態下刀具到工件之間的齊次坐標變換矩陣TgW,即:
由于機床在加工內斜齒輪磨削時各個運動軸會出現幾何誤差,因此還應求出存在誤差時刀具與內斜齒之間的齊次坐標變換矩陣。在存在誤差的情況下,其變換矩陣為
構建機床內斜齒輪磨削系統中刀具到工件坐標系之間的誤差矩陣為EgW,誤差情況下兩坐標系之間的變換矩陣就等于誤差矩陣EgW與理想狀態下兩坐標系之間變換矩陣TgW的乘積,即:
所以
通過最小誤差假設,將EgW表達為
式中:δx、δy、δz分別為幾何誤差在X、Y、Z軸方向上的位移分量,εx、εy、εz分別為幾何誤差在X、Y、Z軸方向上的轉角分量。
1.3 齒面誤差模型
在進行磨削加工過程中,忽略掉砂輪的修整誤差,用η來表示砂輪軸向廓形參數,則修正之后砂輪的軸向廓形坐標矢量為
砂輪的回轉曲面是由其軸向廓形繞軸線做回轉運動所形成的軌跡面。砂輪回轉參數用 φ表示,則在砂輪的坐標系當中,其坐標矢量為
則砂輪單位法矢為
由于砂輪曲面特征可以用單位法矢和坐標矢量聯合表示,因此,在齒輪坐標系中理想的砂輪曲面可表示為
在實際加工中,各軸的幾何誤差用向量G=[x1,x2,···,xm]T表示,故實際的砂輪曲面為
砂輪與齒輪磨削接觸點的條件是:從齒輪坐標系的原點向砂輪回轉面上做一點徑矢rg,若這一點在回轉面上的法線ng與這一點繞齒輪軸線kg的線速度矢量垂直,說明這個點是磨削接觸點。因此,理想的接觸條件與實際的接觸條件分別是:
式中:β是砂輪安裝角,常數;x是砂輪到齒輪的中心距,常數;α是螺旋加工參數,只有在幾何誤差存在時,才會影響到接觸線形狀,而幾何誤差向量G只與各運動軸的位置有關。當α為常數 αk時,f=0 作為接觸條件就只成為與砂輪的軸向廓形 η和回轉廓形參數 φ有關。由于其軸向廓形 η范圍已知,將η等分成n個離散數值,令η=η(j=1,2,3,···,n),根據f=0 求出對應的 φj,然后將(η,φj)代入rg,即可求得接觸點單位法式和坐標矢量。由于η與f=0 聯合求出 φ,因此 η的函數可用 φ來表示,則由n個接觸點擬合成的第k條接觸線也可表示為
而齒面可以看成是由λ條離散的接觸線組成,因此理想和實際齒面分別表示為
故可建立各軸幾何誤差與齒面誤差的關系,模型為
2 加工誤差在線監測及補償
由于數控機床在磨削過程中,會出現不同方向的幾何誤差,機床精度達不到技術規定要求,為了提高機床加工精度,對其加工過程進行在線監測。在機床加工過程中,反饋元件用于在線信息傳遞,可以實現對進給系統的運行狀態和運動精度進行實時監測和控制。
2.1 在線監測
監測目的是通過內置傳感器,完成對信號數據的采集,結合數據處理技術和特征提取方法,將其轉化為可處理信號。在采集過程中,信號數據需進行采樣、編碼和傳輸以便將其輸入到計算機系統中,信息分析、處理、存儲和顯示是通過計算機系統完成的,這些操作可為實時監控提供關鍵的數據。在線監測系統如圖3 所示。
對內斜齒輪進行磨削如圖4 所示,工件參數見表3。加工過程中,C軸旋轉是為了使加工齒輪齒槽處于既定的位置,A軸轉動確定的是加工內斜齒的螺旋角,Z軸方向移動是為了實現齒寬方向磨削的進給運動,在磨削齒槽過程當中,X、Y、A、C軸一直保持鎖止的狀態。
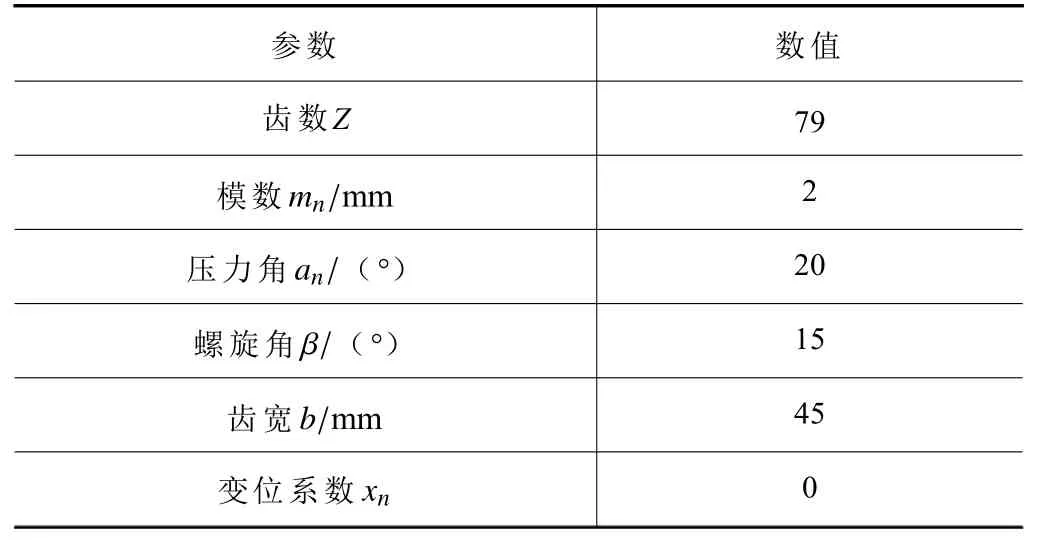
表3 內斜齒輪的參數

圖4 內斜齒輪加工實驗
測試過程中,分別對各軸動態位置信號進行采集,如圖5a 所示。由于受切削刀具與工件相互作用的影響,檢測出X、Z、C軸的位置信號出現了明顯的變化,如圖5b 所示,X軸的跟蹤誤差范圍約為± 0.01 mm,波動幅值微小;Z軸與X軸相比,波動幅值變化較大,跟蹤誤差范圍約為± 0.17 mm;C軸位置在磨削的過程中和Z軸的波動趨勢相似,C軸幅值變化的范圍為± 0.033°。
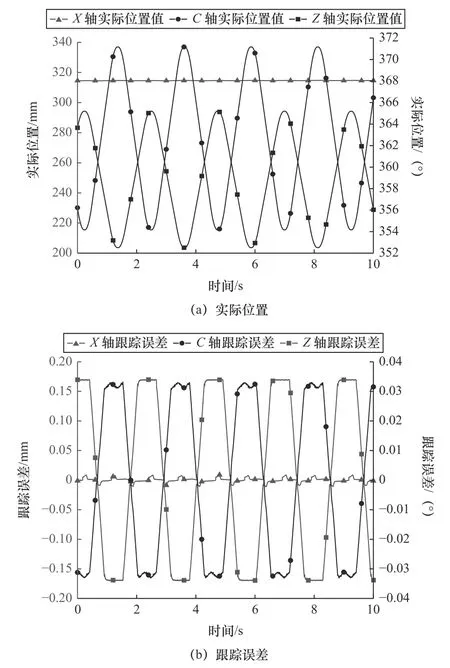
圖5 機床X、Z、C 軸位移信號
2.2 誤差補償
數控機床幾何誤差[15]補償分為硬件補償和軟件補償。硬件補償采用機械式補償來提高其加工精度,該方法成本高、通用性差、設計的周期時間長,并且難以用數控方法進行反饋控制,因此硬件補償在機床的應用中較少;軟件補償是通過對機床各項誤差源研究,配合計算機軟件與數控系統對其進行反向誤差補償,來提高機床的加工精度及性能的。軟件補償基本原理如圖6 所示,在實驗中選用列表法對機床進行誤差補償,不需要改變工件三維模型和機床加工程序,只需要在西門子系統中把測量好的誤差補償值輸入到其誤差補償表里,就能實現誤差修正。
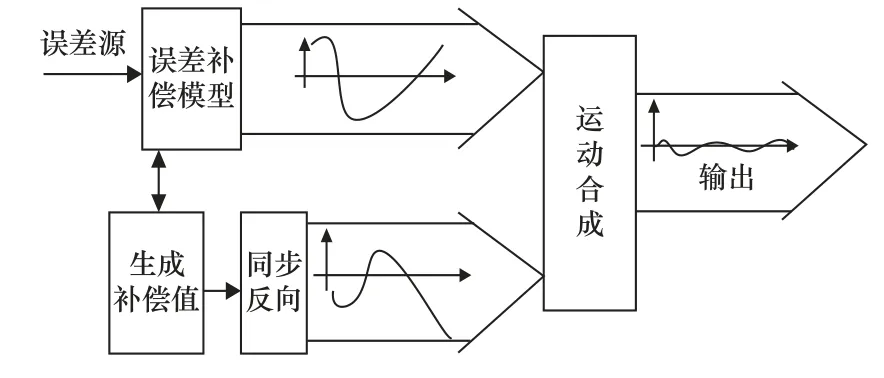
圖6 軟件補償基本原理圖
基于磨削內斜齒加工誤差在線監測,對機床參與運動的軸誤差特性進行測試分析,發現Z、C軸的誤差較大。根據誤差曲線形狀,利用動態操作功能將反向加權補償計算值實時補償到機床軸運動中,對其誤差值進行補償。
3 齒面誤差檢測
為驗證補償后的齒輪精度有所提高,對補償前后的齒輪進行檢測,采用的檢測設備是格里森650GMS,實際測量平臺如圖7 所示。

圖7 內斜齒輪實際測量平臺
內斜齒輪的誤差是按照圓柱齒輪誤差檢測標準進行評定的,用實際數據來表示機床幾何誤差對齒面的影響,分別是內斜齒輪的齒距累積總偏差FP、單個齒距偏差fP和齒廓總偏差Fα等精度標準。對加工內斜齒輪補償前與補償后進行檢測,檢測報告如圖8 和圖9 所示.

圖8 補償前檢測報告
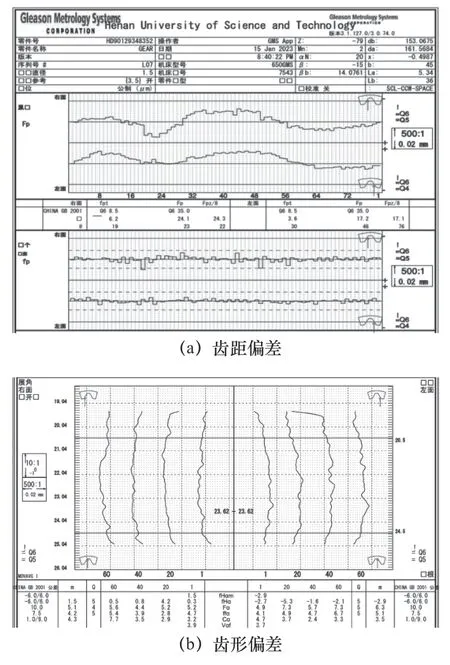
圖9 補償后檢測報告
由表4 可以看出,誤差補償之后內斜齒的加工誤差明顯減少,說明補償后機床的加工精度有了顯著提高。

表4 機床誤差補償前后內斜齒輪精度對比
4 結語
(1)通過齊次坐標變換原理,對工件-床身-刀具進行坐標轉換,建立運動鏈幾何誤差模型。
(2)通過內置傳感器,監測機床在磨削內斜齒輪時各軸的運動狀態,發現機床的X軸誤差幅值波動較小,Z、C軸誤差幅值波動較為明顯,因此,對機床的Z、C軸進行反向誤差補償。
(3)通過齒輪檢測分析儀對補償前后的齒輪進行檢測,經過對比分析,發現補償后的各齒面誤差均有顯著減少。
綜上所述,數控機床在實際加工中各軸均存在幾何誤差,通過機床的在線監測系統和軟件補償,可以提高工件的加工精度和表面質量,對機床加工精度提高具有重要意義。

