基于CCD 的立式五軸機床滑枕多目標優化＊

王松明 廖映華 李 磊 廖鑫宇 李 坤

（四川輕化工大學機械工程學院，四川 宜賓 644002）

滑枕是立式五軸機床的關鍵運動部件，其靜動態特性對整機的加工精度及平順性有重要影響[1]。在工作過程中，滑枕運動到低點時，與軸承座形成豎向的懸臂結構，在切削力作用下易發生共振變形。因此，提高滑枕靜動態特性有利于提高立式五軸機床的加工精度和生產效率。

近年來，隨著精密制造的迅速發展，對立式五軸機床的加工精度提出了更高的要求。為了進一步提高其加工質量，國內外學者對機床的核心部件進行優化研究。劉成穎等以立柱為研究對象結合拓撲優化，并選擇W 型筋板對立柱優化[2]，有效地改善了整機的動態性能；邱自學等運用模糊綜合評價方法實現滑枕改進方案優選，有效提高了滑枕的靜動態特性[3]；謝軍等利用拓撲優化方法對主軸箱結構進行了改進，減少了主軸箱的變形并實現輕量化[4]；張國輝等利用靈敏度分析對橫梁進行多目標優化，提高了橫梁的靜動態特性[5]；Qian Y 等根據機床主軸在不同工況下結合靈敏度分析對主軸進行多目標優化[6]。

以上研究在結構優化方面均取得了一定成效，但大多數研究是對原結構優化改進，忽視了其他結構方案的優選型。考慮到滑枕結構設計變量的復雜性及評價指標的多樣性，以往研究并沒有對滑枕具體筋板方案及相關尺寸進行優化。為此，本文以某型號五軸立式機床的滑枕為研究對象，提出一種筋板布置與響應面法相結合的多目標優化設計方法。在原滑枕結構基礎上，設計出5 種不同內部筋板布置結構，逐一建立滑枕的參數化模型和有限元模型，分別對其進行靜力學和模態分析。以總變形量、1階固有頻率和質量作為評價指標，對有限元仿真數據綜合對比選出井型結構作為優選方案，利用靈敏度分析得出敏感尺寸進行中心組合設計，結合響應面優化，最后進行多目標遺傳算法（multi-objective genetic algorithm，MOGA）優化，優化流程如圖1 所示。

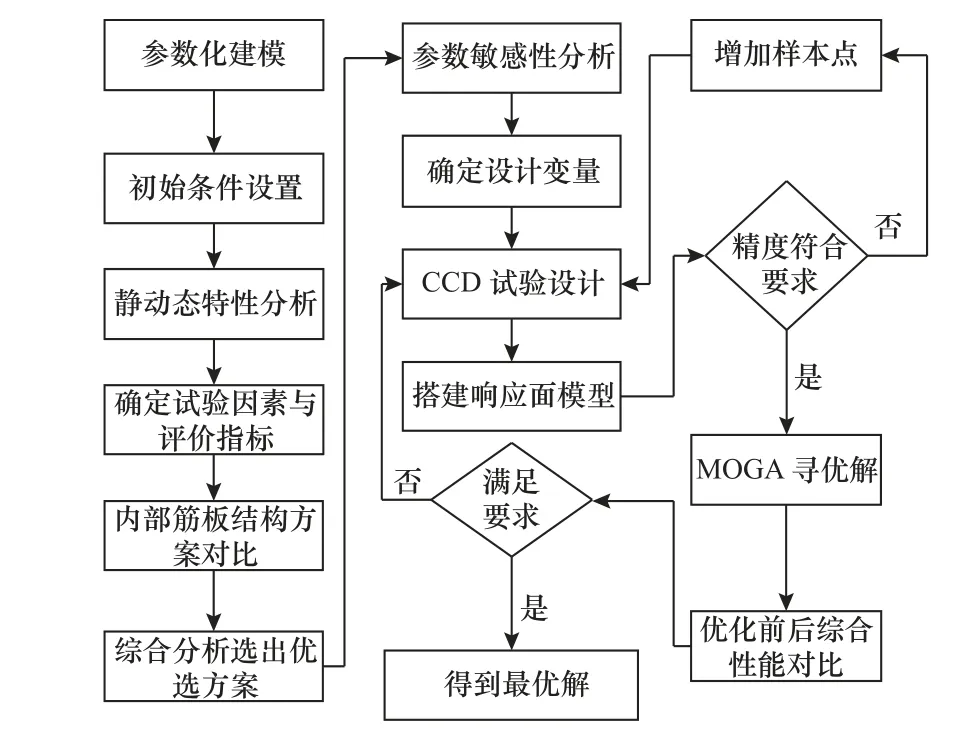
圖1 滑枕分析與優化流程

1 滑枕結構有限元分析

1.1 立式五軸機床結構分析

某型號立式五軸機床（圖2）主要包括床身、A/C轉軸、直線導軌、橫梁、十字滑座、滑枕、工作臺等零部件。在加工時，十字滑座沿著橫梁做X軸運動，橫梁沿前后方向在直線導軌上做Y軸運動，滑枕通過滑塊嵌入十字滑座中沿豎向做Z軸運動。精密高速主軸安裝在滑枕下端，通過主軸上安裝的刀具來對固定在工作臺上的零件進行高速銑削加工。滑枕是立式五軸機床的核心移動件，其靜動態性能直接關系到整機的加工精度。

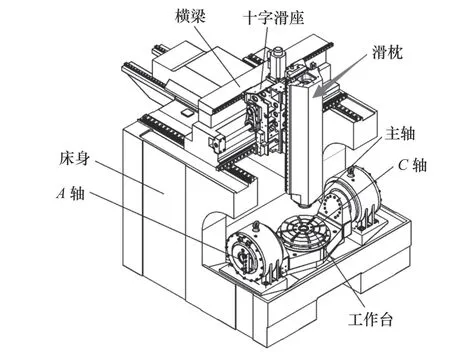
圖2 立式五軸機床結構圖

1.2 滑枕結構有限元分析模型的建立

根據立式五軸機床滑枕組件的實際結構情況，在SolidWorks 繪制參數化模型并導入Ansys Workbench，對滑枕添加實際材料屬性。采用灰鑄鐵HT300 整體鑄造，材料屬性設置見表1。同時，考慮到滑枕內部結構較為復雜，為提高軟件計算效率，根據圣維南原理，對模型的部分特征進行了合理的簡化，壓縮了一些對模擬仿真結果影響較小的細微特征[7]。

表1 材料主要屬性設置

根據滑枕的結構特點，為了滿足計算精度，將網格單元尺寸更改為10 mm，采用自由網格劃分。在進行網格劃分時，還需對網格進行校核，以免解得的數值結果產生過大的誤差。在對滑枕進行了網格劃分后，滑枕有限元網格劃分模型如圖3a 所示。模型的節點數為160 497，單元數為92 654。

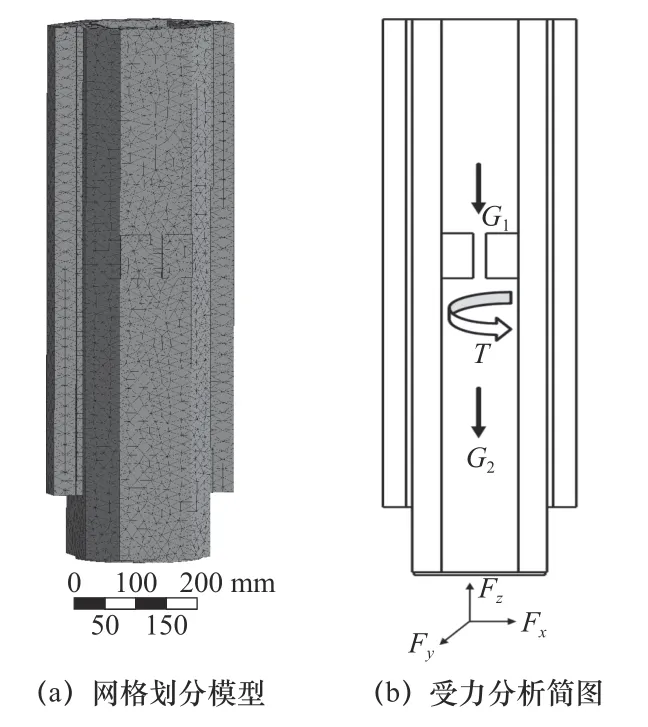
圖3 滑枕結構有限元分析

1.3 邊界條件的設定

有限元分析前處理還需要給模型添加載荷及約束，參考滑枕實際的裝配構造，對軸承座安裝位置施加固定約束，對滑塊導軌位置施加無摩擦支撐。在載荷條件的施加中，應考慮滑枕運動到最低點時，是受力最惡劣的工況。滑枕受到銑削加工刀具前端傳來的主切削力Fc、繞主軸方向的扭矩T及自身重力G1，還受到安裝在滑枕上附屬配件重力G2作用，其受力分析簡圖如圖3b 所示。經過查驗立式五軸機床操作手冊確定具體工況參數為被加工面寬150 mm，每齒進給量0.25 mm，切削深度1.2 mm，銑刀直徑13 mm，銑刀轉速2 200 r/min。滑枕所受到的銑削力可由經驗公式[8]（1）計算得出。

式中：Fc為主切削力；ae為加工寬度；ap為切削深度；fz為每齒進給量；z為刀具齒數；n為刀具轉速；d為刀具直徑；Fx為橫向進給力；Fy為縱向進給力；Fz為垂向進給力。將各參數帶值計算，最終載荷見表2。

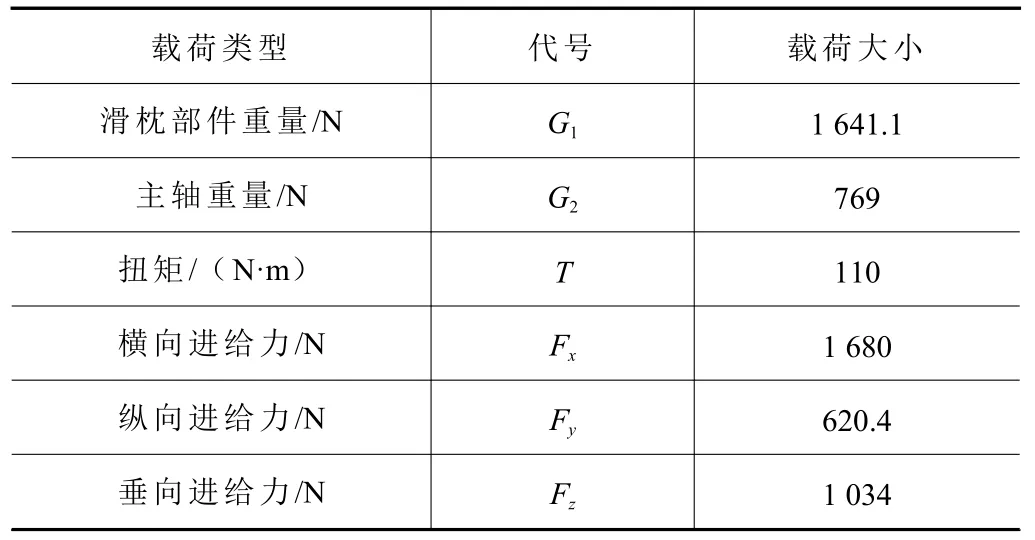
表2 載荷參數取值

1.4 靜力學分析

在上述端銑工況下，對滑枕靜力學特性仿真求解，得到滑枕的綜合變形云圖如圖4a 所示，滑枕的最大總變形量為0.209 89 mm，發生在滑枕的下方端口部位；圖4b 所示為滑枕的等效應力分布云圖，滑枕的最大應力為54.599 MPa，小于灰鑄鐵材料的許用應力335 MPa。由于滑枕引起的變形較大，對整個機床的加工精度有很大的影響，因此，為減小整體的變形，還需要對滑枕結構優化。

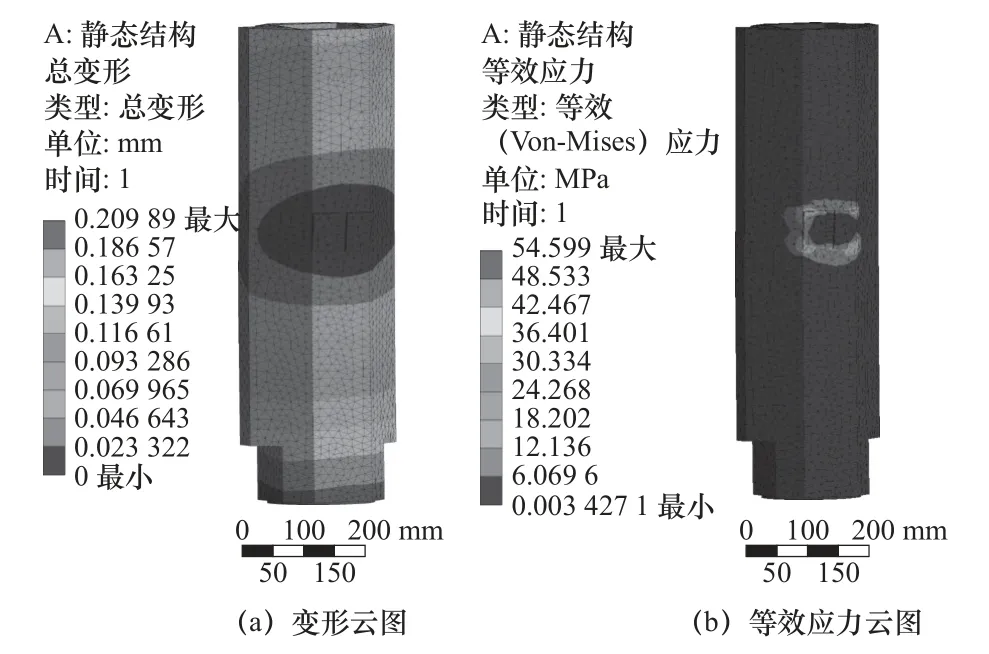
圖4 滑枕靜力學分析結果

1.5 滑枕模態分析

為了明確滑枕結構的振動特性，需要進行模態分析，來判斷其是否與外界激勵的頻率相近，進而預測其是否發生共振。由振動理論可知[9]，低階固有頻率對機械結構的動態特性影響貢獻最大，為此，采用Block-Lanczos 方法，提取了滑枕的前6 階固有頻率和它的振型特點（表3），可知滑枕的1 階固有頻率為85.115 Hz，其1 階模態云圖如圖5 所示。

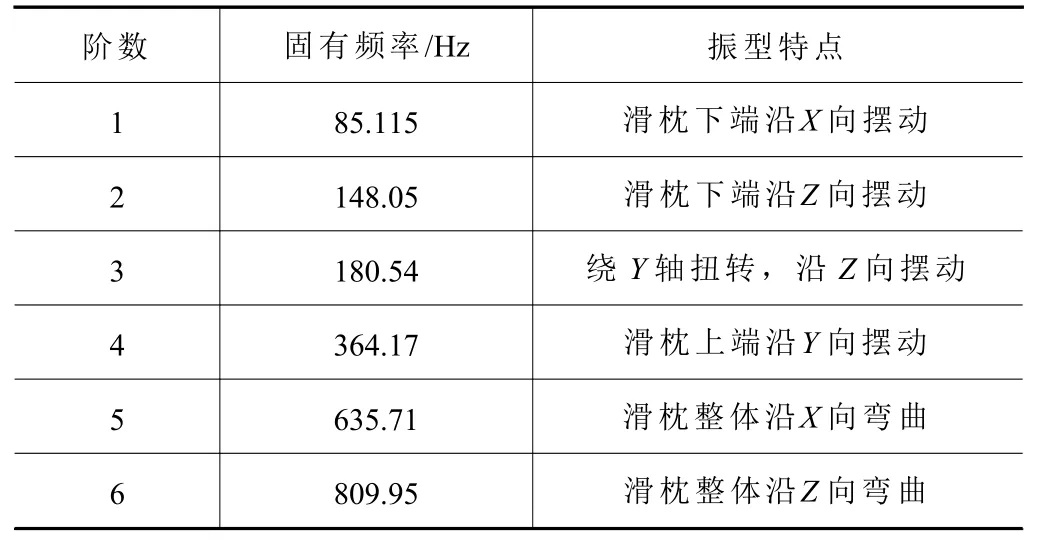
表3 前6 階模態固有頻率及振型的結果

圖5 滑枕1 階模態云圖

當主軸高速運轉時會對滑枕產生激勵作用，電機對滑枕激振頻率計算公式[10]為

式中：f為激振頻率；δ為浮動誤差，一般數值取50；n為電機轉速，最高轉速nmax=2 200 r/min，將以上工作參數代入式（2）可求得fmax=75 Hz。滑枕的1 階固有頻率為85.115 Hz，與最大激振頻率fmax比較接近，容易與主軸形成共振，會影響機床穩定性。因此，為進一步提高立式五軸機床的加工精度，需要提高滑枕的1 階固有頻率。

2 滑枕結構方案的改進與優選

滑枕內部筋板尺寸結構和布置方案對滑枕的各項性能有著重要的影響，基于原滑枕結構筋板布置，設計出井型、米型、蜂型、菱型和X 型5 種改進方案，在SolidWorks 中分別建立三維參數化模型，其內部半剖視圖如圖6 所示。

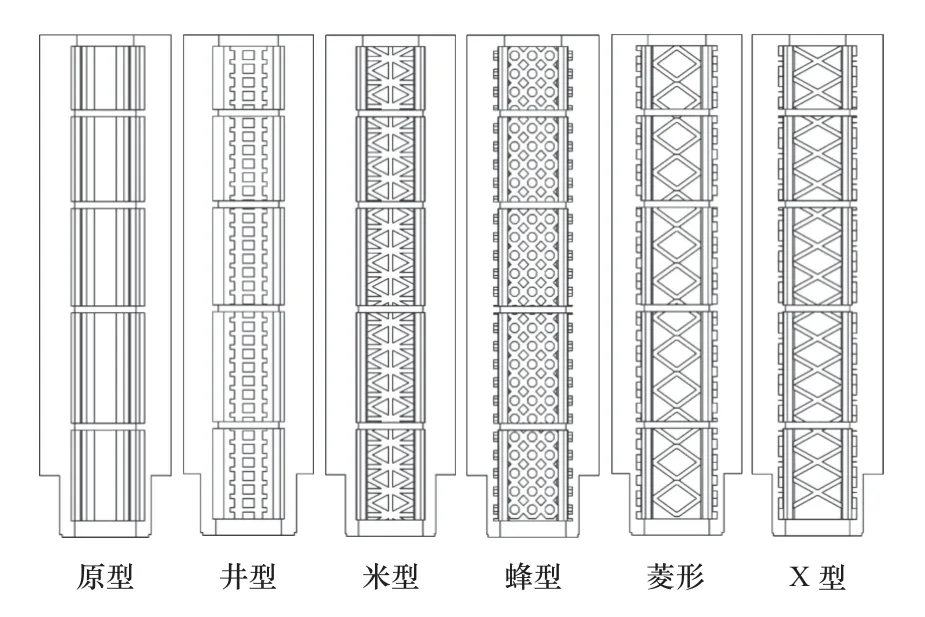
圖6 滑枕內部筋板結構

為了準確、全面地反映各個方案滑枕結構的性能優劣，以1 階固有頻率衡量滑枕的動態性能；選擇最大變形量作為評價指標反映滑枕的靜力學性能；選擇質量作為評價指標反映滑枕的輕量化水平。根據設計的5 種滑枕結構方案，逐一建立相對應的滑枕有限元模型，并進行仿真分析，各個方案滑枕有限元分析結果見表4。

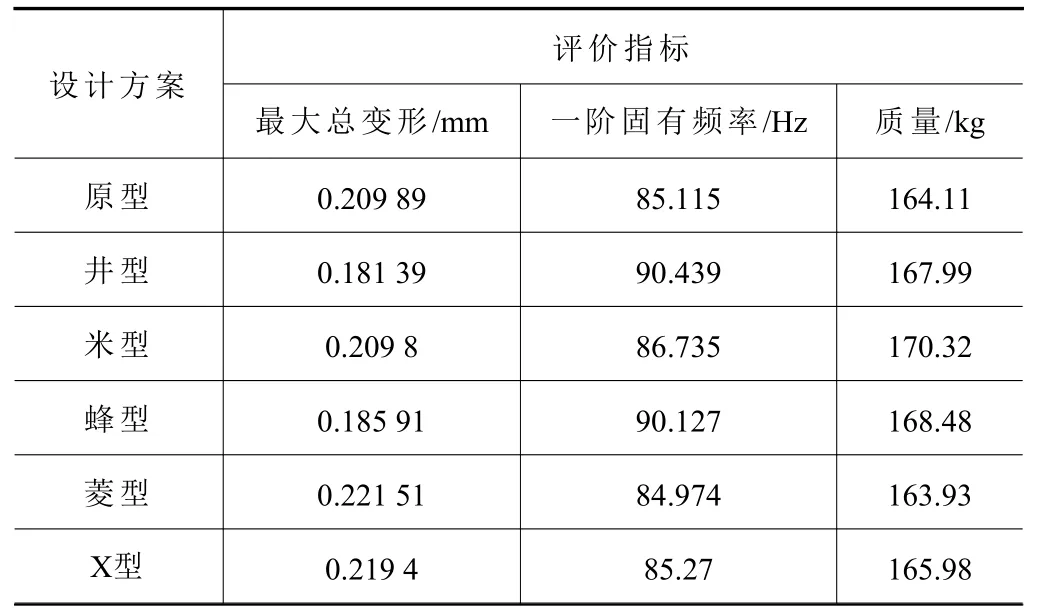
表4 各方案滑枕靜動態性能仿真分析結果

由表4 各方案滑枕靜動態性能仿真分析結果可知，在質量相近的情況下，井型結構的總變形最小為0.181 39 mm，同時其1 階固有頻率最大為90.439 Hz，符合優選條件，因此選取井型結構進行多目標優化。

3 滑枕結構的響應面優化設計

3.1 靈敏度分析

滑枕在結構框架一定時，其尺寸靈敏度的數值能夠體現各個參數對結構性能的影響程度。為滿足實際工況的使用要求，以減小滑枕的總變形量、提高1 階固有頻率為目標，對關鍵尺寸參數進行優選，可以提高后續優化計算效率。選取各個設計變量如圖7 所示。

圖7 滑枕設計變量與取值范圍

根據圖5 所示的滑枕半剖結構簡圖，選取壁厚P1、筋圓半徑P2、橫筋長P3、筋間距P4、圓筋板厚度P5、筋長P6、筋寬P7、端口厚度P8 等8 個關鍵尺寸作為設計變量。表5 列出了各個參數代號、初始值和對應的變化范圍。

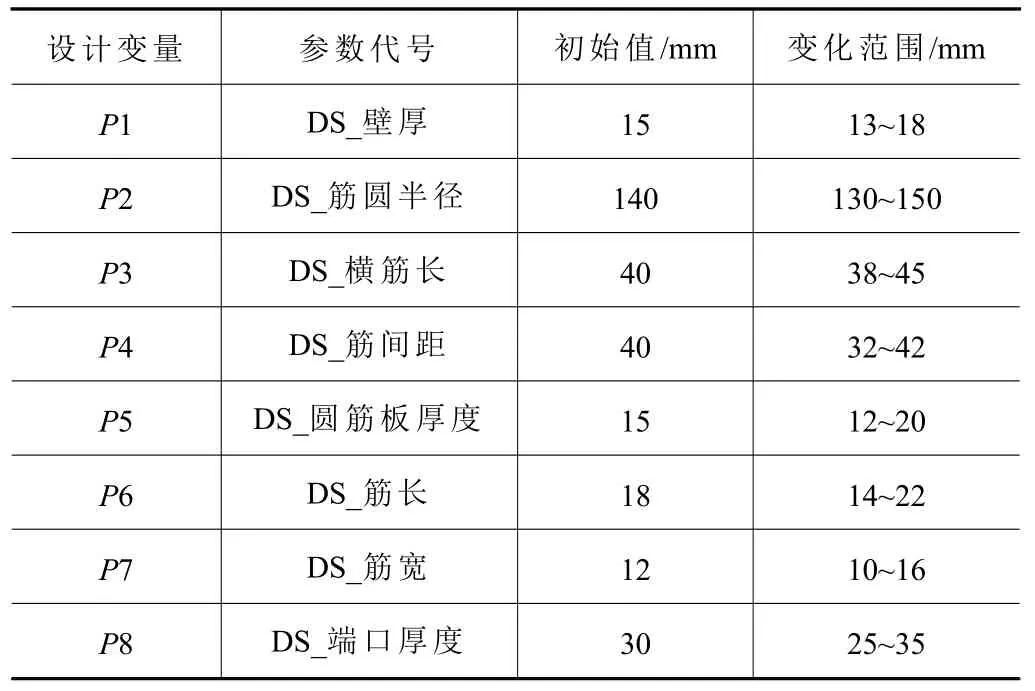
表5 滑枕設計變量與取值范圍

進行參數靈敏度分析，首先在Geometry 中選擇擬定的設計變量，再選取質量、最大總變形量和1 階固有頻率作為輸出量，在Parameters set 可以改變取值范圍，采用Spearman 方法對各參數間的關系進行分析，建立了靈敏度矩陣，以表達輸入量和輸出量之間的相關敏感性。從數學角度上，靈敏度是對函數求偏導，得出各個設計變量對評價指標的貢獻值，靈敏度函數可表示為[11]

完成對滑枕的尺寸參數靈敏度分析（圖8）：P1、P6、P7 對1 階固有頻率和質量的正相關靈敏度較大，P1、P6、P7 對最大總變形量負相關靈敏度較大，其他參數靈敏度絕對值不超過0.2 可忽略。由此，后續選取P1、P6、P7 這3 個尺寸參數作為滑枕結構關鍵尺寸進行優化。

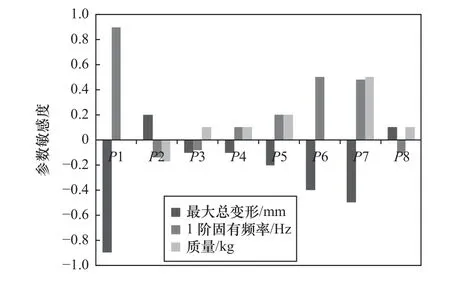
圖8 參數靈敏度分析

3.2 試驗設計

文中采用中心組合設計方法來自動劃分并選取設計點，CCD 由分部試驗設計演變而來[12]，選取P1、P6、P7 這3 個尺寸參數作為設計變量，得到15 組不同實驗方案，具體樣本數據及試驗結果見表6。

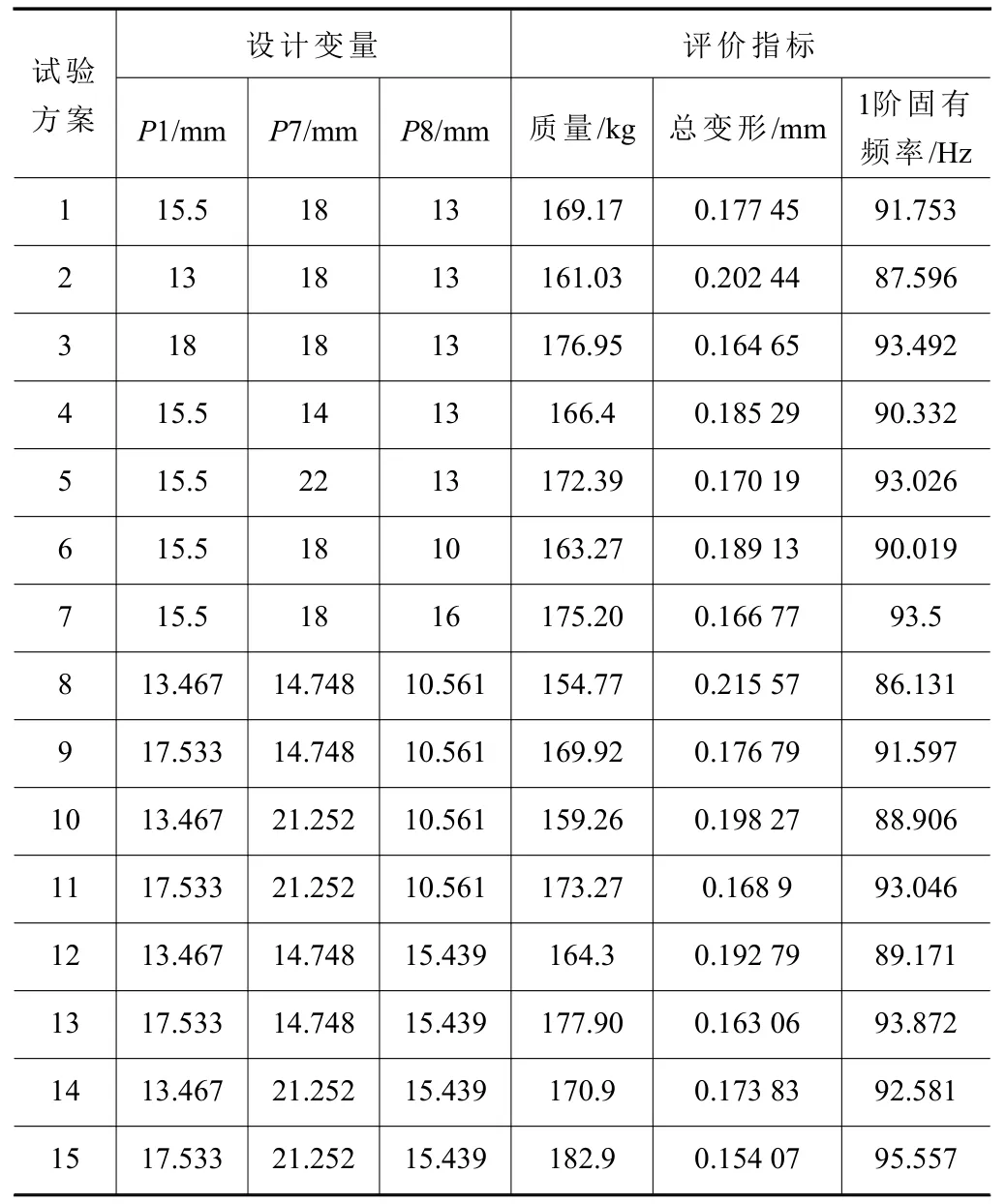
表6 CCD 試驗樣本設計

3.3 響應面法分析

響應面法通過合理的試驗方法對所得設計點進行試驗，得設計變量對目標函數的響應值并構造響應面[13]，將其運用到有限元分析中。通常響應面模型采用二次多項式，對于m個變量，響應面模型y(x)為

式中：X為設計變量向量；xi為設計變量；C0、Ci、Cii、Cij為未知系數，其個數N=(m+1)(m+2)/2。

基于收集的樣點數據，采用多目標遺傳算法建立響應曲面的模型[14]。圖9 是響應面擬合優度圖，可見，總變形量、1 階固有頻率及質量的樣本點均位于y=x函數圖像附近，表明設計樣本點與響應面吻合程度高。

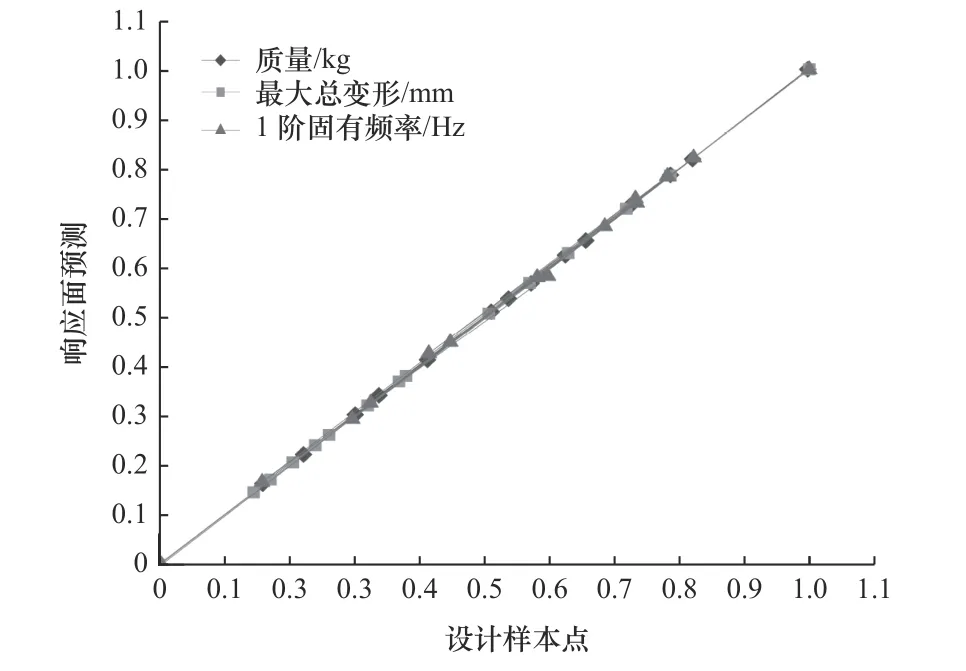
圖9 響應面擬合優度圖

圖10 所示為P1、P6、P7 與它們的模型特性之間的響應面曲線，可以看出，滑枕的設計變量與1階固有頻率呈非線性關系（圖10a），與總變形量和質量近似為線性關系（圖10b 和圖10c）。

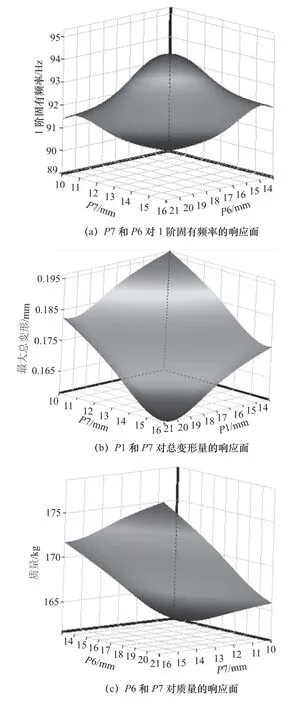
圖10 響應面模型

3.4 基于多目標優化求解

文中采用多目標遺傳算法，由非支配排序遺傳算法Ⅱ推演而來[15]。為尋找全局最優解，必須預先設置目標函數、設計變量和約束條件。以滑枕總變形量最小、1 階固有頻率最大及質量最小作為優化的3 個目標，該多目標優化數學模型可表示為

式中：pi為設計變量，i=1,2,3；m(pi)為滑枕的質量函數；σ(pi)為最大變形量函數；f(pi)為1 階固有頻率函數。多目標遺傳算法的設置參數見表7。

表7 MOGA 的參數設置

通過MOGA 優化后，可以得到滑枕參數帕累托最優解。由于設計變量取值是在自上而下的設計過程中關聯得到的，尺寸不成整數，為了便于實際生產，需要對優化尺寸進行圓整，其圓整結果見表8。

表8 設計變量圓整結果

3.5 優化結果分析驗證

重新建立滑枕有限元模型并進行仿真，由優化后滑枕的變形云圖（圖11a）與1 階模態振型云圖（圖11b）可知，最大總變形量為0.161 1 mm，1 階固有頻率為94.385 Hz。

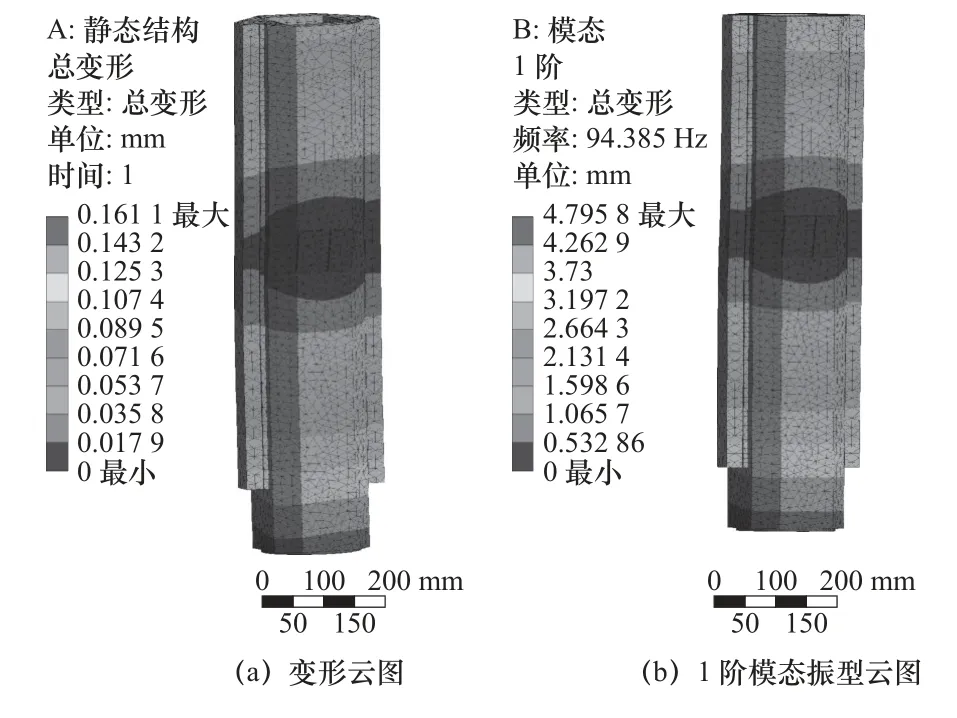
圖11 優化后滑枕的變形云圖與1 階模態振型云圖

滑枕優化前后的評價指標對比結果見表9。通過對滑枕井型結構方案的多目標優化，在滑枕總質量僅增加3.32%的情況下，其最大總變形減小23.25%，一階固有頻率增加10.89%，證實了該優化方案的可靠性。

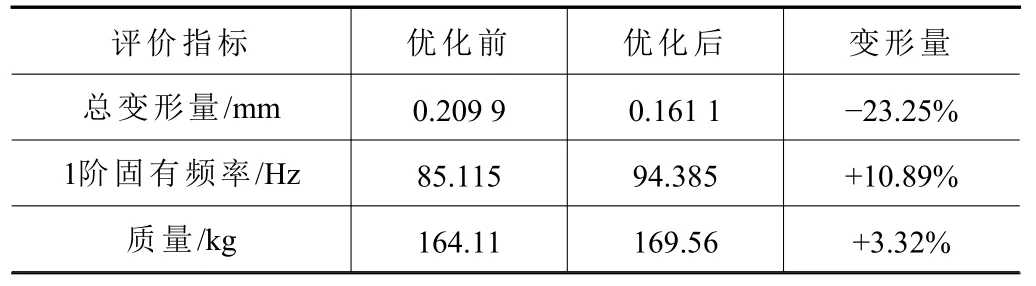
表9 滑枕優化前、后評價指標對比

4 結語

（1）本文在滑枕筋板布置優選方案基礎上，提出了一種基于CCD 的響應面法與多目標優化相結合的方法，根據原滑枕結構，設計出5 種不同筋板結構布置，設立方案評價指標，逐一進行靜力學分析和模態分析，根據質量、最大總變形量和1 階固有頻率3 個評價指標綜合比對分析，選出井型結構作為最佳方案。

（2）對井型結構尺寸參數進行靈敏度分析選出關鍵尺寸，利用多目標遺傳算法取最優參數解。優化結果表明：與原結構相比，在總質量增加3.32%的情況下，其最大總變形減小23.25%，1 階固有頻率增加10.89%，取得良好的優化效果。同時也驗證了該優化方法的合理可靠。