試驗臺支承對滑動軸承動特性系數識別精度的影響研究＊

徐 帆 唐 杰 陳潤霖 杜 辰 崔亞輝 劉 凱

（西安理工大學機械與精密儀器工程學院，陜西 西安 710048）

滑動軸承被廣泛應用于多個工業領域，具有承載力大、穩定性好等優點[1-2]，目前已經具備了較為完整的理論體系[3-5]。但是隨著旋轉機械設備的性能提升，對滑動軸承的動特性提出了更高要求，通過試驗獲取軸承動特性變得尤為重要[6]，但是動特性測試過程容易受到各種因素的干擾，從而引入測試誤差，導致最終識別的動特性系數與真實值相差甚遠[7]。

滑動軸承的動特性識別就是通過測試手段獲取軸承的剛度阻尼系數，常用的方法包括脈沖激振識別法[8]、錘擊法[9]、正弦激振法[10]和多頻激振法[11]等。Wang L 等[12]采用非接觸式諧波激勵法和附加不平衡激勵法分別進行了高速水潤滑動靜壓軸承的動特性系數的識別，并將實驗結果和理論預測進行了對比。袁小陽等[13]用多頻技術來識別油膜的動特性系數，提出了振動響應或固有頻率評價法和軸承系統失穩評價法。王永亮等[14]根據軸頸擾動與非線性油膜力的關系，利用等幅異頻位移激勵技術識別油膜的動特性系數。馬石磊等[15]設計和搭建了一種軸承轉子系統實驗臺，用不平衡質量法識別軸承的動特性系數。

這些測試結果與理論值都存在一定的誤差，大多未考慮滑動軸承動特性測試過程中由于外界干擾引入的誤差，包括測試儀器系統誤差、數據處理誤差等[7-16]。Wu Q Y 等[17]提出了一種新型磁懸浮動態標定方法，利用力和位移的雙通道聯合標定，能夠在一定程度上減小測試儀器帶來的誤差，避免靜態標定的不足[18-19]，但是仍然無法完全消除測試系統中其他元件和連接產生的誤差[20-21]。這樣，殘余誤差對動特性系數的識別精度仍然有影響，且影響程度與動特性試驗臺本身的參數有關[22]。

本文針對滑動軸承倒置式試驗臺，采用仿真方法模擬軸承動特性測試過程，重點分析試驗臺支承剛度和支承阻尼的大小對軸承動特性系數識別精度的影響，為滑動軸承動特性試驗臺建設和測試參數選取提供必要的數據支持。

1 滑動軸承倒置式試驗臺方案及動特性識別方法

1.1 試驗臺及測試方案

滑動軸承倒置式試驗臺方案如圖1 所示，轉子在驅動力的作用下旋轉。除潤滑系統和驅動系統等輔助系統外，試驗臺主體部分主要由試驗軸承系統、靜載系統、動載系統和支承系統組成。試驗軸承為滑動軸承，該系統的支撐裝置主要是滾動軸承。

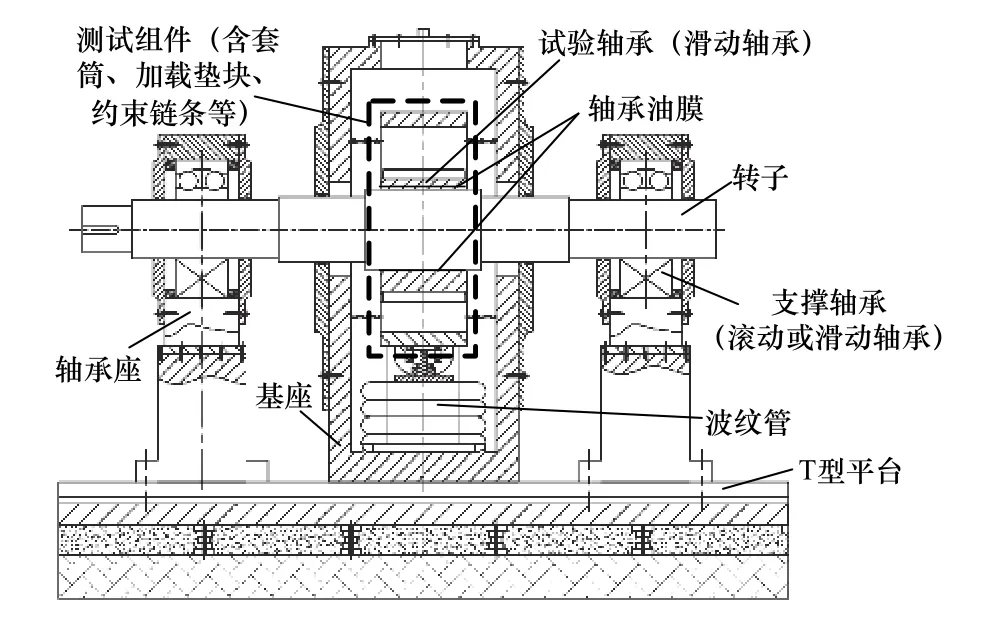
圖1 倒置式軸承動特性試驗臺方案

1.2 動特性識別方法

在考慮系統的連接剛度和連接阻尼的情況下，該試驗臺系統的動力學模型如圖2 所示，以單頻兩次激振法為例，假設所施加的激振力矢量通過軸承的幾何中心，且軸承作平面平行運動。(X01,Y01)為激振力F1作用下試驗軸承相對于靜平衡位置的絕對位移；(X11,Y11)為試驗軸承處轉子的絕對位移；(X21,Y21)為試驗軸承軸孔中心相對轉子軸心的位移。(X02,Y02)為激振力F2作用下試驗軸承相對于靜平衡位置的絕對位移；(X12,Y12)為試驗軸承處轉子的絕對位移；(X22,Y22)為試驗軸承軸孔中心相對轉子軸心的位移。其中，試驗軸承軸孔中心相對轉子軸心的位移與試驗軸承處轉子的絕對位移之和為試驗軸承相對于靜平衡位置的絕對位移，由此，可以消掉公式中的(X11,Y11)和(X12,Y12)。

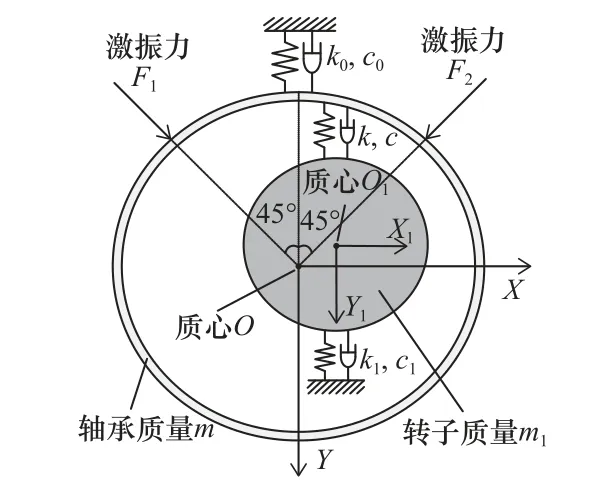
圖2 倒置式試驗臺的動力學模型

當只有F1作為激振力時，可得到試驗臺系統的運動微分方程，見式（1）。

當只有F2作為激振力時，可得到試驗臺系統的運動微分方程，見式（2）。

式中：F1和F2為激振力；m、m1分別為試驗軸承和轉子質量；k、c為試驗軸承的剛度阻尼系數矩陣；k0、c0為試驗臺連接剛度阻尼系數矩陣；k1、c1為轉子支承的剛度阻尼系數矩陣。

考慮到方程的獨立性，對式（1）和式（2）均取第一個微分方程進行傅里葉變換，然后整理得到滑動軸承動特性系數測量方程（3）。

式（3）即為滑動軸承動特性系數測量方程，方程左邊即為待求參數k、c，方程右端為測試過程中獲得的激振力和位移信號，然后對已經獲得的激振力和位移信號進行傅里葉變換，得到幅值和相位，利用幅值和相位數據計算F、X的實部和虛部，代入式（3），令其實部和虛部分別對應相等，可得到8 個線性方程，從而求解出滑動軸承的8 個動特性系數，完成動特性系數的識別。

2 滑動軸承動特性系數的識別精度仿真評估方法

滑動軸承的動特性識別是根據試驗臺的激振力和振動響應來反求軸承的動特性系數，本文根據試驗臺系統的正反動力學問題，提出滑動軸承動特性系數識別精度的仿真評估方法，如圖3 所示。首先已知試驗臺系統的激振力及油膜剛度阻尼矩陣k、c，可以求解出在激振力F1和F2作用下軸承相對于平衡位置的相對振動響應及相對于轉子軸心的絕對振動響應，其中F1作用下軸承相對振動的幅值和相位分別為Ax21、Ay21和φx21、φy21，絕對振動的幅值和相位分別為Ax01、Ay01和φx01、φy01；F2作用下相對振動的幅值和相位分別為Ax22、Ay22和φx22、φy22，絕對振動的幅值和相位分別為Ax02、Ay02和φx02、φy02。

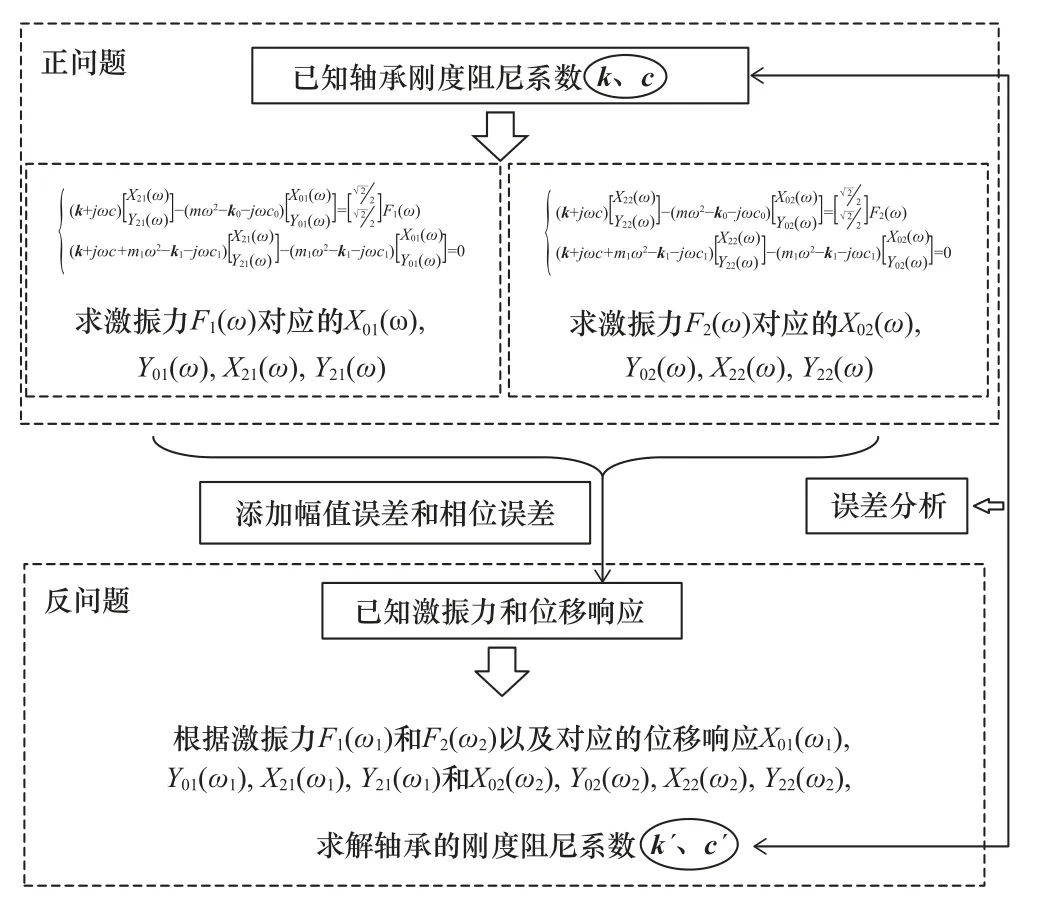
圖3 基于正反動力學問題的動特性系數識別精度評估方法

在實際測試過程中，由于測試儀器硬件和環境的干擾，測試獲取的信號與真實信號之間存在誤差，這種測試誤差主要包括幅值誤差和相位誤差，將測試誤差直接添加到仿真得到的位移數據中，用于模擬真實振動測試數據，即：

式中：Am0、Am為添加誤差前后信號的幅值；φ、φ0為添加誤差前后信號的相位；aA、aφ分別為幅值的相對誤差和相位的絕對誤差。

根據動特性識別的求解算法，將添加測試誤差的振動信號作為輸入，可識別出軸承的剛度阻尼系數矩陣k′、c′，將其與試驗臺軸承的剛度阻尼的設定值k、c進行對比，可評估軸承動特性系數的識別精度為

式中：εk為剛度系數識別誤差；εc為阻尼系數識別誤差。

3 試驗臺支承對軸承動特性系數識別精度的影響分析

3.1 試驗臺參數

本文所研究的滑動軸承倒置式試驗臺系統參數見表1，根據一般滑動軸承動特性測試的實際情況，設置測試過程中存在+5%的幅值誤差和+1o的相位誤差[18]。

表1 倒置式軸承動特性試驗臺的參數

3.2 支承剛度的影響分析

試驗軸承的主剛度為kxx，主阻尼為cxx，當試驗臺支承剛度為表1 中初值的0.001～1 000 倍時，在激振頻率為0～1 000 Hz 時，試驗臺支承剛度對軸承動特性系數的影響規律分別如圖4 和圖5 所示。為方便分析，將圖分為A、B、C、D 這4 個部分，分別代表不同頻率和不同支承剛度時對應的主剛度和主阻尼識別誤差。

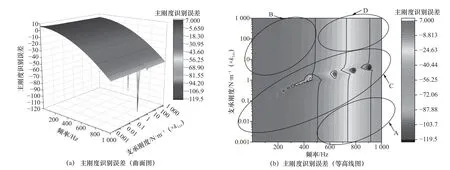
圖4 不同支承剛度時軸承主剛度識別誤差

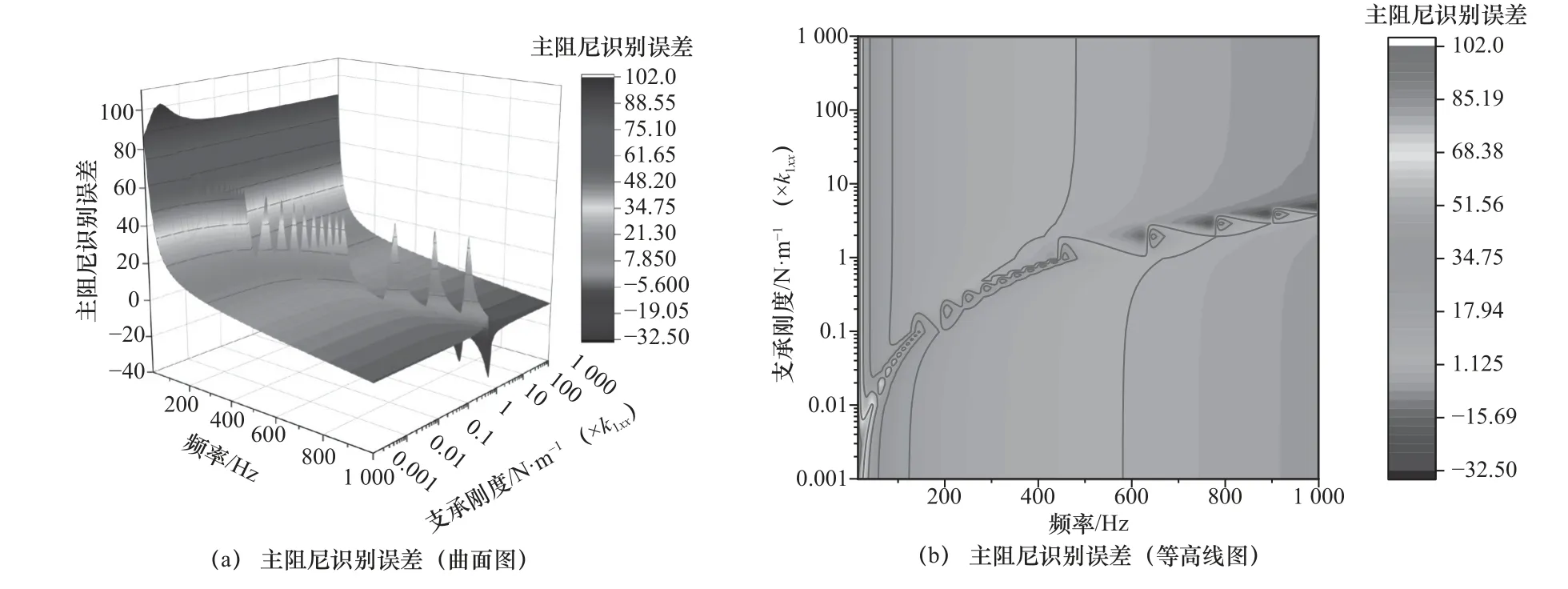
圖5 不同支承剛度時軸承主阻尼識別誤差

從圖4 中可以看出，在B 區域，即頻率比較小、支承剛度比較大時，此時主剛度識別精度比較好；在A、D 區域，當頻率增大后，無論支承剛度大小，其識別精度都有所下降；在C 區域，軸承主剛度識別誤差存在較大波動，主剛度識別精度較差。

從圖5 可以看出，在B 區域，即頻率比較低時，此時主阻尼識別精度比較好；在A、D 區域，頻率比較高時，明顯可以看出，主阻尼識別誤差有所增大；在C 區域，軸承主阻尼識別誤差存在較大波動，主阻尼識別精度較差。

若將上述識別誤差圖的4 個部分分為3 個等級，識別精度“較好”部分表示為“++”，識別精度“次之”部分表示為“+”，精度“很差”部分表示為“-”，當支承剛度變化時，試驗臺支承剛度對軸承動特性系數識別精度的影響規律總結見表2。

從表2 中可以看出，B 部分剛度阻尼識別精度較高，所以支承剛度在B 部分選取比較合適，支承剛度的選取范圍大概為試驗臺支承剛度的1～1 000 倍，大小為7.452×108～6.9×1011N?m-1，激振頻率的選取范圍大概在30～400 Hz。

3.3 支承阻尼的影響分析

若支承阻尼為倒置式試驗臺支承阻尼的0.001～1 000 倍，在激振頻率為0～1 000 Hz 時的動特性識別精度分別如圖6 和圖7 所示。為方便分析，將圖分為A、B、C、D、E 這5 個部分，分別代表不同頻率和不同支承阻尼時對應的主剛度和主阻尼識別誤差。

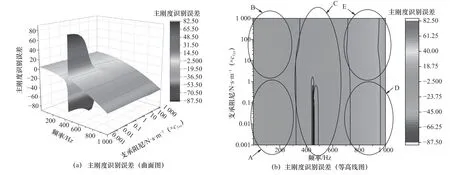
圖6 不同支承阻尼時軸承主剛度識別誤差

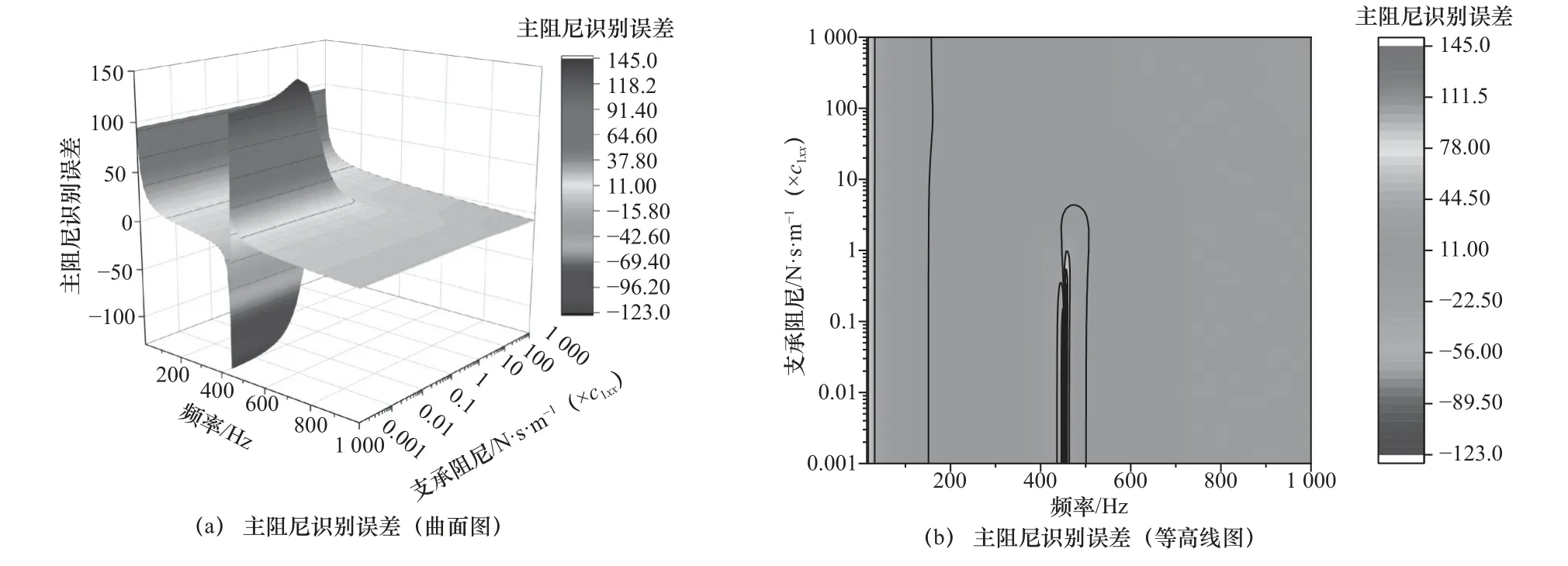
圖7 不同支承阻尼時軸承主阻尼識別誤差

從圖6 中可以看出，在A、B 區域，即頻率比較小時，此時主剛度識別精度比較好，在D、E 區域，當頻率增大后，無論支承阻尼大小，其識別精度都有所下降，在C 區域，軸承主剛度識別誤差存在較大波動，主剛度識別精度較差。

從圖7 可以看出，在A、B 區域，即頻率比較低時，此時主阻尼識別精度比較好，在D、E 區域，頻率比較高時，主阻尼識別誤差有所增大，在C 區域，軸承主阻尼識別誤差存在較大波動，主阻尼識別精度較差。

若將上述識別誤差圖的5 個部分分為3 個等級，識別精度“較好”部分表示為：“++”，識別精度“次之”部分表示為“+”，精度“很差”部分表示為“-”，當支承阻尼變化時，試驗臺支承阻尼對軸承動特性系數識別精度的影響規律總結見表3。由表3 可以看出，A 和B 部分剛度阻尼識別精度較高，所以支承阻尼在A 和B 部分選取都比較合適，也就是說支承阻尼對動特性識別精度的影響幾乎可以忽略，激振頻率的選取范圍大概在30～280 Hz。

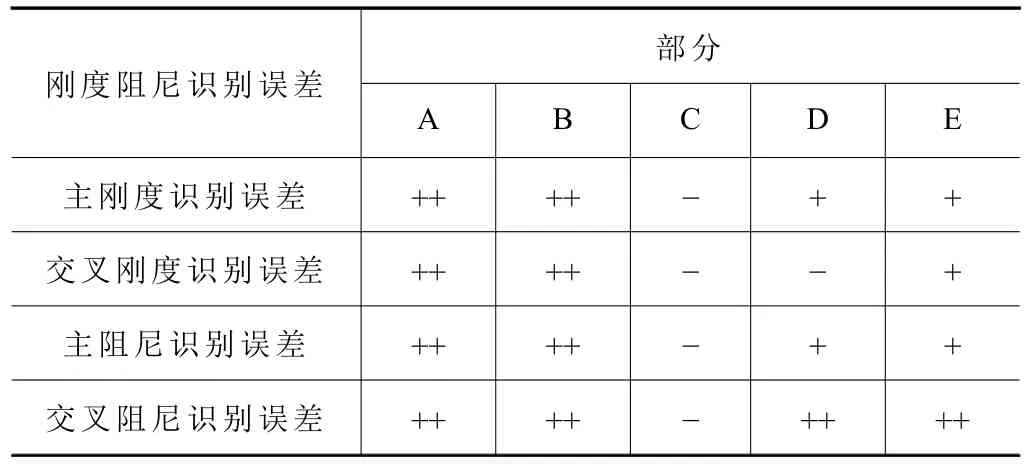
表3 剛度阻尼識別誤差等級表

4 結語

（1）以倒置式軸承動特性試驗臺為研究對象，建立了試驗臺的動力學模型，根據軸承動力學正反問題，采用仿真的方法模擬了動特性測試的過程，并提出了測試誤差對軸承動特性系數識別精度的評估方法。

（2）分析了考慮激振頻率時支承參數對動特性系數識別精度的影響規律，重點分析了不同條件下滑動軸承主剛度以及主阻尼的識別誤差大小，并根據識別誤差絕對值對激振頻率和支承參數的取值范圍進行了等級劃分。

（3）針對本文研究的倒置式軸承動特性試驗臺，激振頻率取值為30～280 Hz，支承剛度的取值應大于試驗軸承的剛度，而支承阻尼影響不大，可以任意取值。在此參數條件下，滑動軸承動特性系數的識別精度受殘余誤差影響較小，抗干擾能力較強。