融合正逆程特征的GRU 神經網絡關節遲滯特性建模研究＊

黨選舉 張一晨

（①桂林電子科技大學電子工程與自動化學院,廣西 桂林 541004；廣西智能綜合自動化高校重點實驗室,廣西 桂林 541004）

傳統工業機器人在諸多領域得到廣泛的應用，但是在3C、醫療和無人零售等需要柔性作業的場景中，傳統工業機器人無法滿足特殊的工作要求，因此，輕型工業機器人應運而生[1]。為了滿足在未知環境中工作的安全性，在輕型工業機器人中引入柔性，但柔性關節執行器表現出的復雜遲滯特性，嚴重影響了關節的動態性能和傳動精度[2]。因此，除采用高精度制造技術外，遲滯特性的高精度建模是通過補償控制提高輕型工業機器人傳動精度的重要途徑之一。

輕型工業機器人關節遲滯特性產生的原因復雜，關節柔性[3]、非線性摩擦[4]、齒輪背隙[5]和裝配誤差[6]等都會使關節產生復雜的遲滯特性。文獻[7]使用廣義Maxwell 模型、Preisach 模型和多項式方法對關節中的非線性摩擦和間隙進行綜合建模。但模型對非對稱的復雜遲滯特性沒有適用性。文獻[8]在Bouc-Wen 模型的基礎上增加了一個具有方向性的修正項，解決了由摩擦導致的能量損失的不確定性。但預測精度受到參數辨識算法的影響，需要在精度和計算復雜度之間做出權衡。柔性關節遲滯特性受到很多因素的影響表現出高度非線性，基于遲滯經典建模方法很難應對所有影響因素。

基于數據驅動的建模方法通過研究系統的相關數據，能夠獲取其中的規律。機器學習算法具有強大的非線性映射能力和泛化能力，可以學習到數據中的抽象規律，已成為主流的數據驅動方法[9]，并在遲滯建模領域得到應用[10]。文獻[11]使用簡單動態遲滯算子（SDHO）來描述不同頻率下的遲滯特性，并將該算子與混沌神經網絡組成串聯結構，通過實驗驗證了模型優于PI 算子與混沌神經網絡的串聯結構。文獻[12]在證明對角遞歸神經網絡（dRNN）特定條件下具有與Preisach 相同的遲滯特性[13]的基礎上，提出了一種新的損失函數以保證dRNN 的每個神經元在訓練過程中都參與遲滯特性的建模。文獻[14]使用有記憶性的VSM 對遲滯特性進行建模，并通過WNN 提取Volterra 核。該模型利用VSM 的記憶性簡化了對神經網絡輸入空間的擴展，并且有效描述遲滯特性的頻率相關性。可見，基于數據驅動的整體建模方法可以有效描述由多種因素引起的復雜遲滯特性。

直接將神經網絡運用到遲滯建模中無法準確描述遲滯特性，文獻[15]提出一種多分支BP 神經網絡模型可以有效避免神經網絡遲滯建模過程中的過擬合現象。文獻[16]在循環神經網絡的基礎上，將遲滯模型分成了遲滯子模型和頻率子模型，使模型能夠準確描述遲滯特性的頻率相關性。上述文獻在建模過程中沒有直接考慮遲滯所表現出的多值對應和極值點特性（非光滑特征），通過間接方式考慮遲滯相關特性，設計的結構復雜的遲滯模型，不利于工程應用。

機器人關節遲滯特性建模需要依賴多種傳感器的支持，文獻[17]構建了關節輸出角度與關節輸出轉矩之間的遲滯非線性關系，用于描述不同剛度下的關節輸出轉矩。文獻[18]針對機器人關節中表現的遲滯特性，構建了磁流變離合器中電流與轉矩之間的遲滯非線性特性，并提出了一種轉矩補償算法，提高了柔性關節的控制精度。上述文獻中的關節遲滯特性建模方法，以機器人關節配置轉矩傳感器為前提，不適用于未配置負載轉矩傳感器的低成本輕型工業機器人柔性關節遲滯特性建模。

本文針對低成本輕型工業機器人柔性關節遲滯特性建模，構建了一種融合正逆程特征的GRU 神經網絡遲滯模型。關節執行器未安裝負載轉矩傳感器而無法采用轉矩-扭轉角之間的關系描述關節遲滯非線性，本文采用電機驅動電流-扭轉角，間接描述關節遲滯特性。通過數據驅動的建模方法，利用基于卡爾曼濾波的電流增量，提取正程和逆程的特征，并與GRU 神經網絡相融合，構建了一種融合正、逆程特征的GRU 神經網絡遲滯模型。將歷史預測信息作為模型輸入構建動態GRU 神經網絡遲滯模型，其結構簡潔，具有較高的模型精度。

1 GRU 神經網絡遲滯模型

輕型工業機器人柔性關節執行器的遲滯特性是指關節執行器在往復運動中，輸出轉矩與關節扭轉角之間表現出的多值對應關系。這種多值對應關系受到歷史輸入信號的極大值或極小值的影響，具有記憶性。所以，具有一定的記憶能力的神經網絡模型，適合于對遲滯特性的建模。

1.1 門控循環單元

門控循環單元（gate recurrent unit，GRU）[19]是為了解決時間序列長期記憶問題所提出的結構，其特有的重置門和更新門可以對歷史數據記憶或遺忘，可以避免遲滯建模過程中擴展輸入空間。相較于RNN，GRU 在處理長時間序列問題時，具有更長的記憶且不容易發生梯度爆炸或梯度消失。GRU具有的門結構較LSTM 更少，可以用較少的計算量達到與LSTM 相同的效果[20]。

GRU 單元結構如圖1 所示，每個GRU 單元具有2 個門結構，更新門zj(k)和重置門rj(k)，以及1個隱藏狀態h?j(k)，共同決定了GRU 單元的記憶能力。

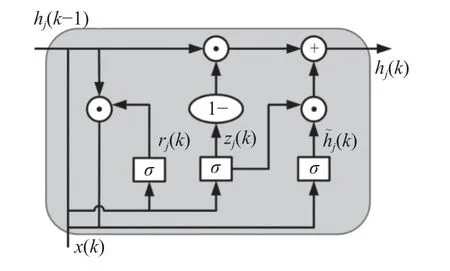
圖1 GRU 單元結構圖

輸入信號x(k)∈Rm，表示k時刻的m個輸入信號，GRU 單元的數學表達見式（1）～式（4）。

更新門：

式中：zj(k)表示k時刻更新門的輸出值，h(k-1)表示k-1時刻n個GRU 單元的輸出值構成的n維向量，即h(k)=(h1(k),h2(k),···,hj(k),···,hn(k))T，其中Wz∈Rn×m和Uz∈Rn×n表示更新門的權值矩陣，表示更新門的偏置量，σ表示sigmoid 函數，(·)j表示第j個元素。

重置門：

式中：rj(k)表示k時刻第j個GRU 單元的重置門的輸出值，Wr∈Rn×m和Ur∈Rn×n表示重置門的權值矩陣，表示重置門的偏置量。

隱藏狀態：

GRU 單元輸出：

式中：hj(k)表示k時刻第j個GRU 單元的輸出值。

1.2 GRU 神經網絡遲滯模型的構建

圖2 是單輸入單輸出的GRU 神經網絡（GRUNN）遲滯模型結構圖。將n個GRU 單元的輸出值加權求和組成GRU 神經網絡遲滯模型的輸出層：

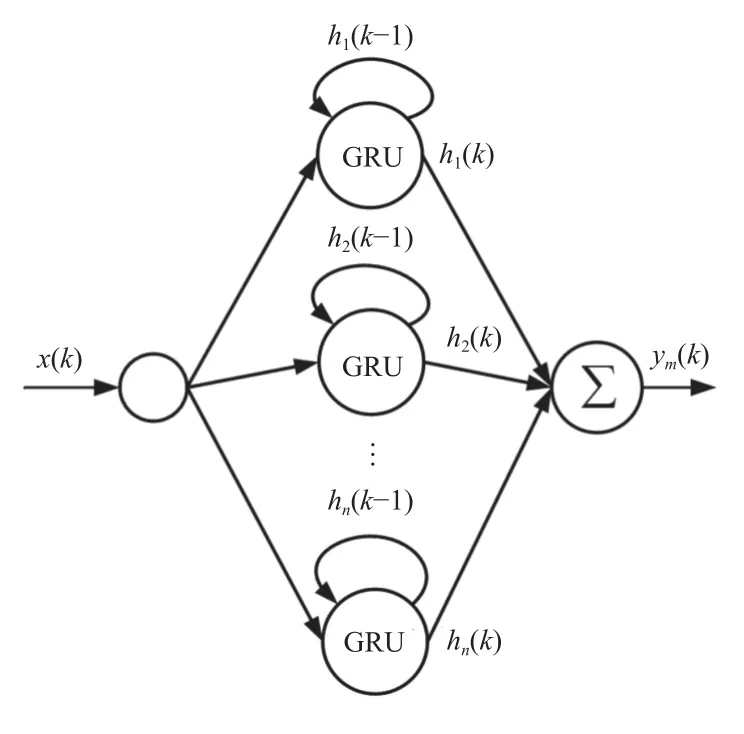
圖2 GRU 神經網絡遲滯模型結構圖

式中：ym(k)表示k時刻GRU 神經網絡遲滯模型輸出層的輸出值，Wy∈Rn表示輸出層的權值。

使用沿時間反向傳播算法對權值進行更新，其損失函數：

式中：E(k)表示k時刻的損失函數值，yd(k)表示k時刻的目標值，E表示訓練數據總的損失函數值。

GRU 神經網絡遲滯模型的記憶能力有利于解決遲滯特性對歷史輸入信號的依賴，因此本文以GRU 神經網絡遲滯模型為基礎，進一步考慮遲滯特性正、逆程及極值信息，將關節特有的遲滯特征融入其中，成為柔性關節遲滯特性高精度建模的關鍵。

2 融合正逆程特征的GRU 神經網絡遲滯模型

2.1 柔性關節遲滯特征分析

結合圖3 和圖4 對遲滯特性所具有的多值特性和極值點的特征進行分析。圖3 中箭頭表示遲滯特性隨著時間增加而變化的趨勢，輸入信號隨時間增加而增加稱為遲滯特性的正程，輸入信號隨時間增加而減小稱為遲滯特性的逆程。其中，位于正程的p1點和位于逆程的p2點的輸入信號大小相等，均為x1，輸出信號卻對應2 個不同的值，分別是y1和y2。遲滯特性在相同的輸入值x1下對應不同輸出值y1和y2的情況，被稱為多值對應。

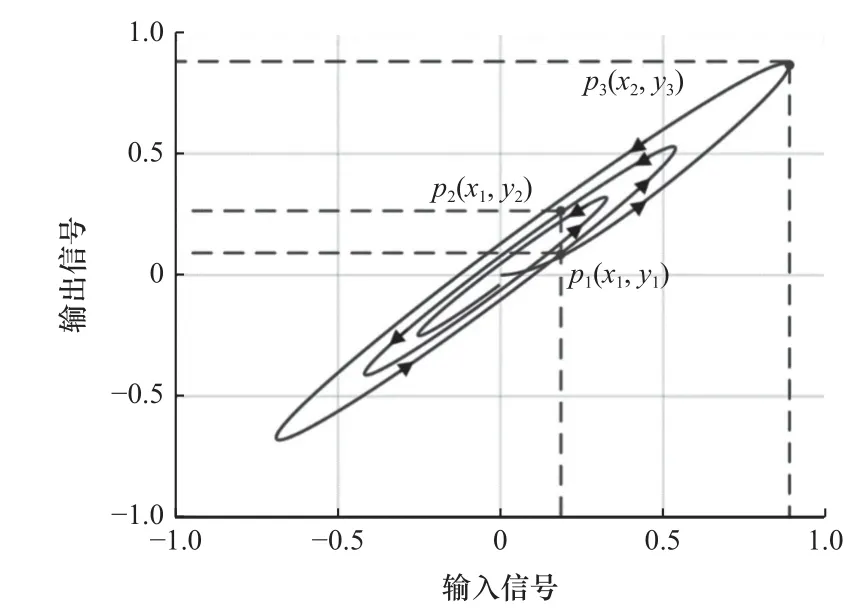
圖3 遲滯特性多值對應示意圖

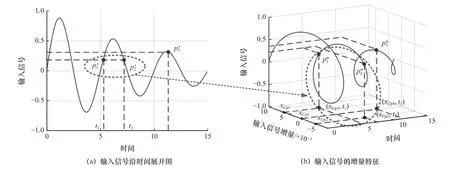
圖4 輸入信號增量作為正逆程特征

2.1.1 多值對應的特征提取

利用輸入信號的增量作為區分遲滯特性輸入信號正程和逆程不同變化趨勢的特征。將不同時間下相同的輸入信號通過不同的增量加以區別，并作為輸入信號的特征輸入神經網絡。

2.1.2 極值點的非光滑性特征弱化

在遲滯特性曲線的轉折點，將圖3 中的p3點作為遲滯特性的極值點，通常是建模誤差較大的位置。通過輸入信號的增量特征將p3點對應到圖4b 中點，輸入信號的增量特征在同一周期的正程和逆程中，極大值點是由輸入信號的正增量逐漸變化到零，而極小值點是由輸入信號的負增量逐漸變化到零，通過增量的正負區分遲滯特性曲線中的極大值和極小值不同變化趨勢，連續變化的增量減緩了極值點處的非光滑性，使極點趨于可導。

2.2 正逆程特征的提取

未安裝負載轉矩傳感器的低成本機器人柔性關節執行器無法使用轉矩與扭轉角之間的關系描述關節遲滯特性。考慮到電機驅動電流隨負載對應變化的特性，本文選取關節電機驅動電流與扭轉角之間的遲滯特性作為建模數據，間接描述負載變化導致的柔性關節遲滯特性。

電流傳感器采樣得到電機驅動電流包含測量帶來的干擾信息。為了提取機器人柔性關節電流與扭轉角之間遲滯特性的正、逆程特征，需要將實際采樣的輸入電流信號進行預處理。

式中：KF(·)表示卡爾曼濾波，濾波后的值為xf(k)。將濾波后的殘差信號(x(k)-xf(k))進行頻域分析可得，電流傳感器采樣到的信號x(k)包含高斯白噪聲，使得神經網絡很難穩定到期望輸出，導致建模精度下降。數據預處理結果如圖5 所示，卡爾曼濾波可以有效濾除輸入電流信號中的高斯白噪聲。為了從輸入電流信號中獲得清晰的增量特征，需要對濾波后的結果進行處理。

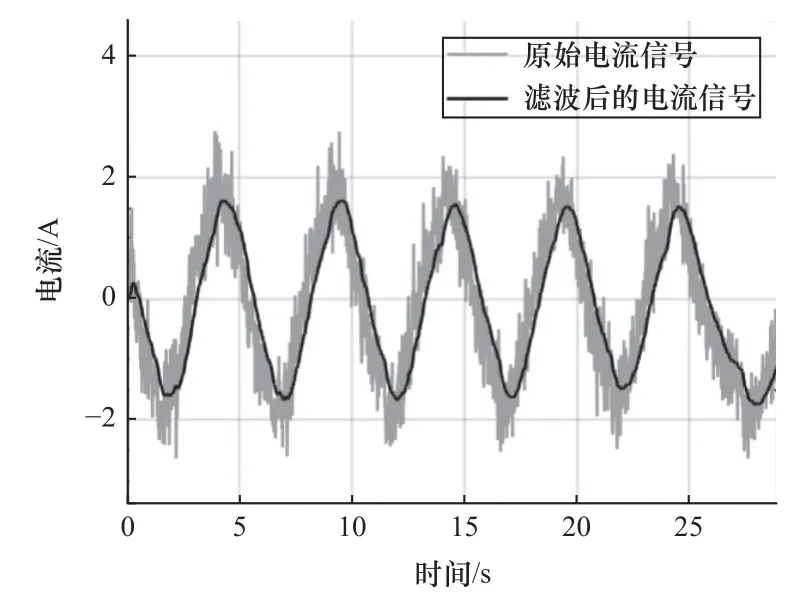
圖5 實際采集電流數據的預處理結果

式中：xff(k)表示第二次卡爾曼濾波后的結果，式（9）表示對xff(k)求增量，結果表示為?xff(k)。為了從輸入電流信號中獲得清晰的增量特征，將xf(k)再次通過卡爾曼濾波進行處理。如圖6 所示，第二次卡爾曼濾波處理前后信號增量特征的變化對比可得，第二次卡爾曼濾波很好地平緩了xf(k)中增量特征的波動。但計算信號的增量會放大高頻干擾，引入不必要的噪聲，需要進一步對增量特征?xff(k)處理。

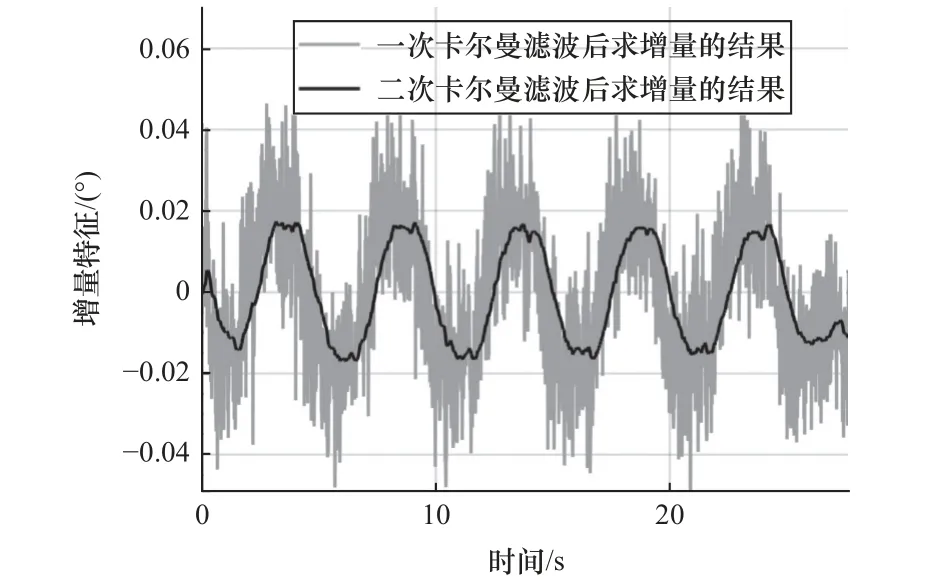
圖6 第二次卡爾曼濾波前后增量的變化對比圖

式中：xc(k)表示具有遲滯正、逆程特征信息的增量特征。使用xff(k)的增量?xff(k)描述輸入信號在遲滯正程和逆程不同的變化趨勢，并將?xff(k)使用卡爾曼濾波進行處理。卡爾曼濾波可以有效濾除計算增量帶來的高頻噪聲，處理結果如圖7 深色曲線所示，得到的xc(k)作為描述遲滯正、逆程變化的特征輸入神經網絡。

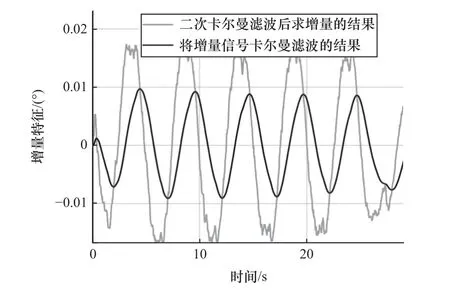
圖7 增量信號卡爾曼濾波前后對比圖

2.3 融合正逆程特征的GRU 神經網絡遲滯模型的構建

融合正、逆程特征提取的GRU 神經網絡遲滯模型的整體框圖如圖8 所示，其中正、逆程特征提取如圖8 虛線框所示。

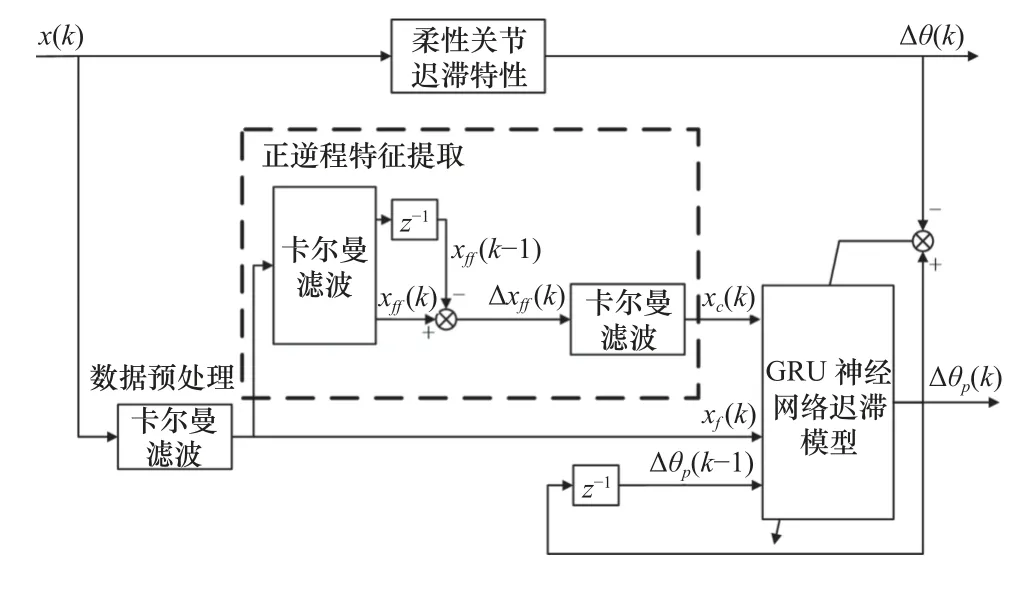
圖8 融合正逆程特征的GRU 神經網絡遲滯模型框圖

所提出的遲滯模型有3 個輸入信號，分別是：

（1）正、逆程特征的輸入信號xc(k)，其作用是提取輸入電流信號在正程和逆程中不同的變化趨勢。

（2）數據預處理后的電流信號xf(k)，其作用是將去除掉高斯白噪聲的電流信號輸入GRU 神經網絡。

（3）將GRU 神經網絡遲滯模型的扭轉角預測結果?θp(k)的歷史值?θp(k-1)作為神經網絡的輸入，構建動態的GRU 神經網絡遲滯模型。在GRU 神經網絡遲滯模型中，融入了柔性關節遲滯特性特有的多值特性和極值點非光滑特性，這個實現是提高關節遲滯特性的高精度建模的關鍵。

3 實驗結果與分析

3.1 實驗驗證

所搭建的輕型工業機器人GLUON 實驗平臺如圖9 所示。為了保證用于關節遲滯建模的數據具有代表性，選擇機械臂第二關節（ID：2）從零位（如圖9 中機械臂的位姿）開始進行往復運動，并以100 Hz 左右的采集頻率對建模所需的電流信號和扭轉角信號進行記錄。

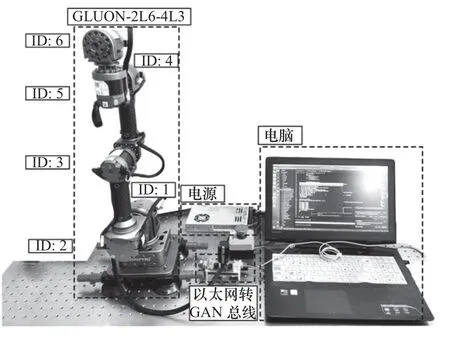
圖9 GLUON 實驗平臺

實驗比較了2 種模型的預測結果，GRU 神經網絡遲滯模型（圖2）和融合正、逆程特征的GRU 神經網絡遲滯模型。

兩種模型中GRU 神經網絡的結構相同，使用20 個GRU 單元作為神經網絡隱藏層節點，使用相同的訓練數據分別訓練。由于機器人關節在大角度周期運動過程中可選擇的頻率范圍并不大，所以使用不同的運動周期去代替描述頻率的不同。使用周期為5 s、8 s、10 s 的正弦衰減信號作為機器人關節運動的激勵信號，并采集關節往復運動中電流和扭轉角作為訓練數據。兩種模型使用相同的數據訓練完成后，分別對6 s、9 s、13 s 的數據進行預測，對比預測結果。

3.2 不同頻率下的遲滯模型預測結果

用于提取不同周期預測數據的機器人關節的運動軌跡分別為周期6 s、9 s、13 s 的正弦衰減信號，以驗證模型對不同頻率且帶有次環的關節遲滯特性的預測效果。

機器人關節在周期為6 s 的正弦衰減運動軌跡下，采集到的遲滯數據如圖10 中實線所示。GRU神經網絡遲滯模型的預測結果如圖10a 中虛線所示，對應預測均方誤差和最大誤差分別為2.16 和3.74 °。融合正、逆程特征的GRU 神經網絡遲滯模型的預測結果如圖10b 中虛線所示，其預測均方誤差和最大誤差分別為0.07 和1.05 °。圖11 和圖12 分別為預測結果的時域展開對比和誤差對比圖。

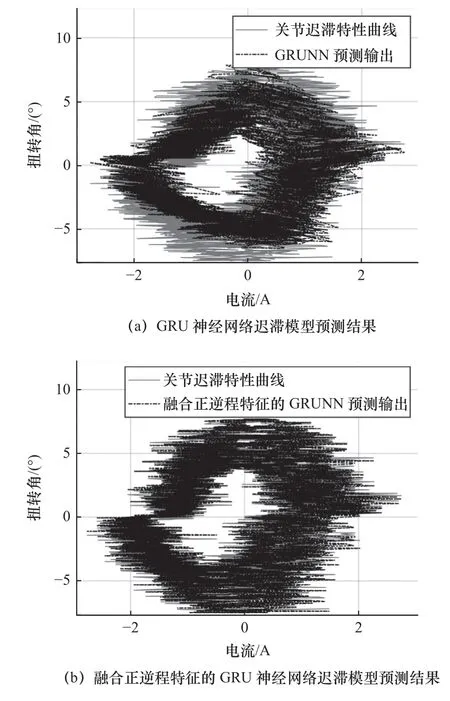
圖10 周期為6 s 的遲滯特性預測結果對比圖

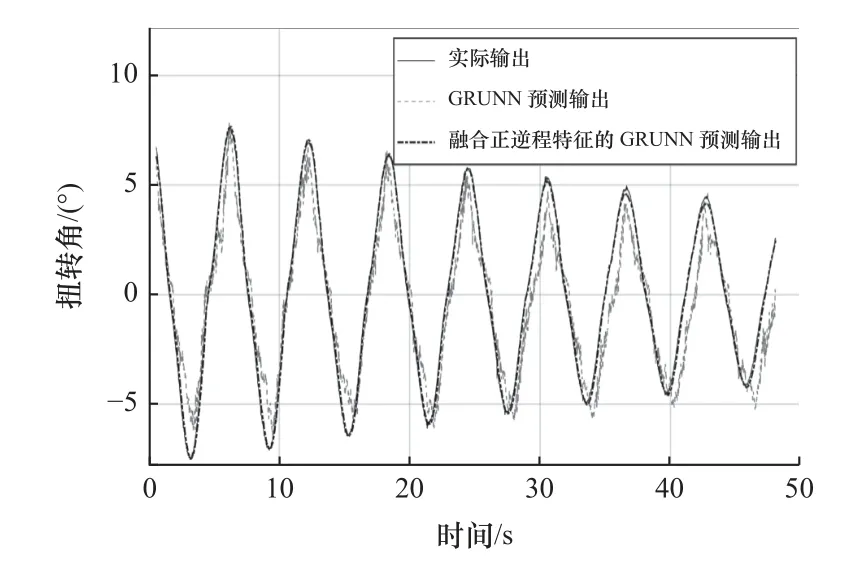
圖11 周期為6 s 的遲滯特性預測輸出的時域展開對比圖

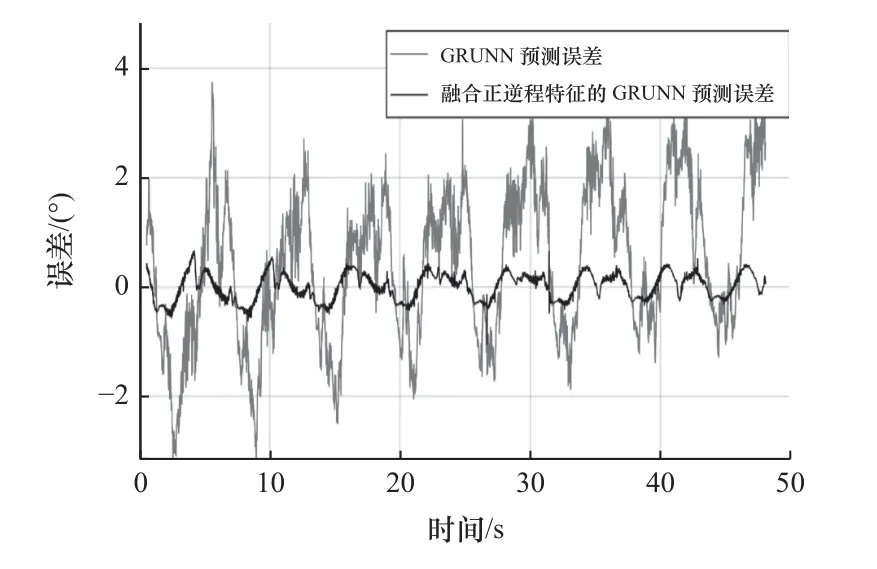
圖12 周期為6 s 的遲滯特性預測誤差對比圖

機器人關節在周期為9 s 的正弦衰減運動軌跡下采集到的遲滯數據如圖13 所示，其中，GRU 神經網絡遲滯模型的預測結果如圖13a 中虛線所示，預測均方誤差和最大誤差分別為0.66 和2.63 °。融合正、逆程特征的GRU 神經網絡遲滯模型的預測結果如圖13b 中虛線所示，預測均方誤差和最大誤差分別為0.01 和0.53 °。圖14 和圖15 分別為預測結果的時域展開對比和誤差對比圖，融合正、逆程特征的GRU 神經網絡遲滯模型的預測誤差更小。

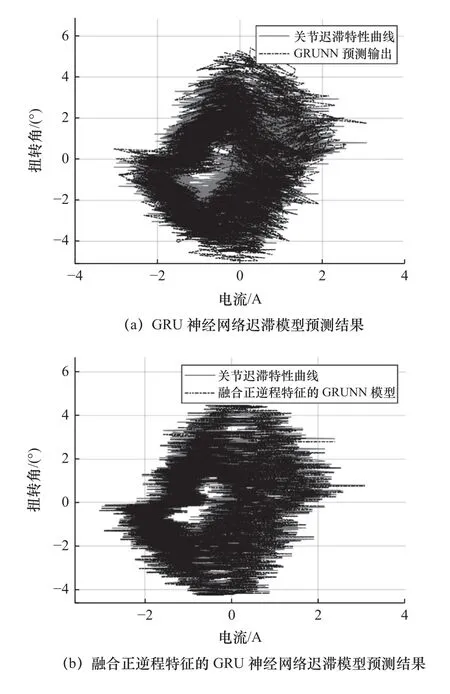
圖13 周期為9 s 的遲滯特性預測結果對比圖

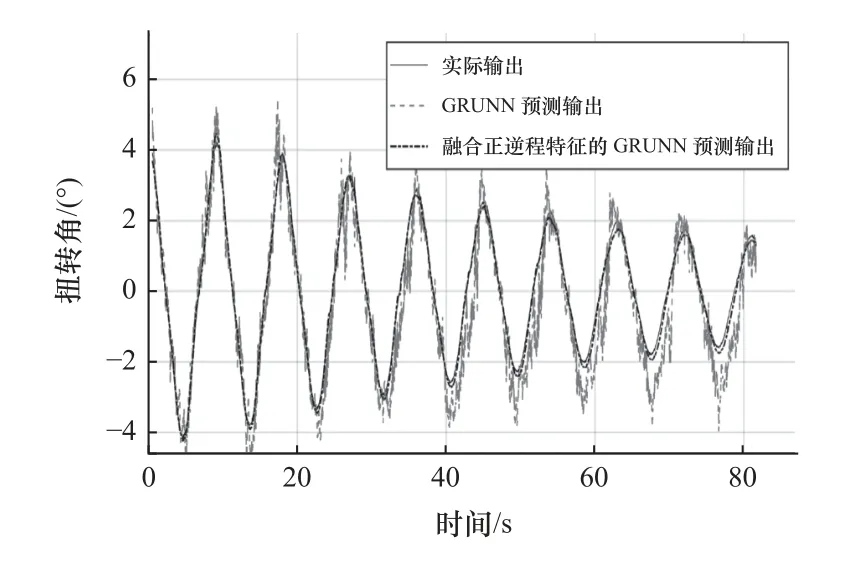
圖14 周期為9 s 的遲滯特性預測輸出的時域展開對比圖

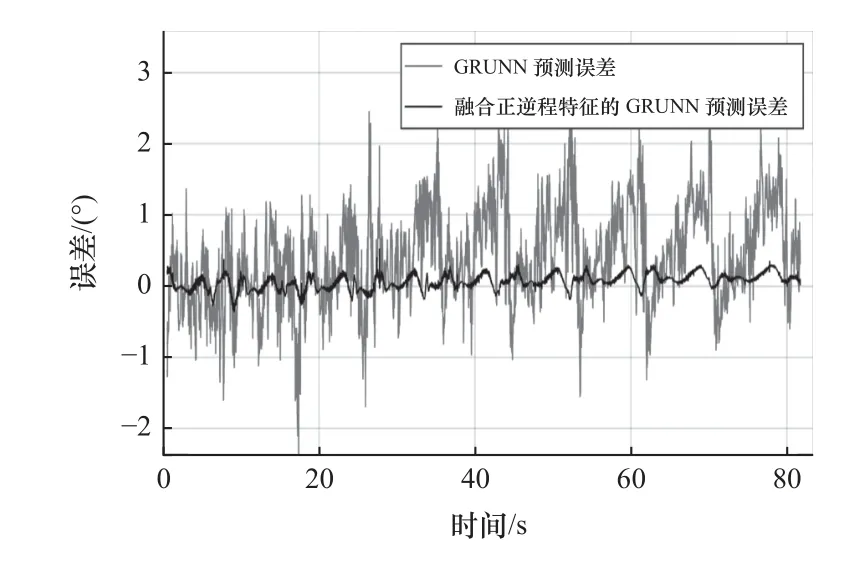
圖15 周期為9 s 的遲滯特性預測誤差對比圖

機器人關節在周期為13 s 的正弦衰減軌跡運動下采集到的遲滯數據如圖16 中實線所示，圖16a中虛線所示是GRU 神經網絡遲滯模型的預測結果，其預測均方誤差和最大誤差分別為0.93 和4.23 °。融合正、逆程特征的GRU 神經網絡遲滯模型的預測結果如圖16b 中虛線所示，預測均方誤差和最大誤差分別為0.01 和0.40 °。圖17 和圖18 分別為預測結果的時域展開對比和誤差對比圖。從圖中誤差對比可知，融合正、逆程特征的GRU 神經網絡遲滯模型預測誤差明顯降低。

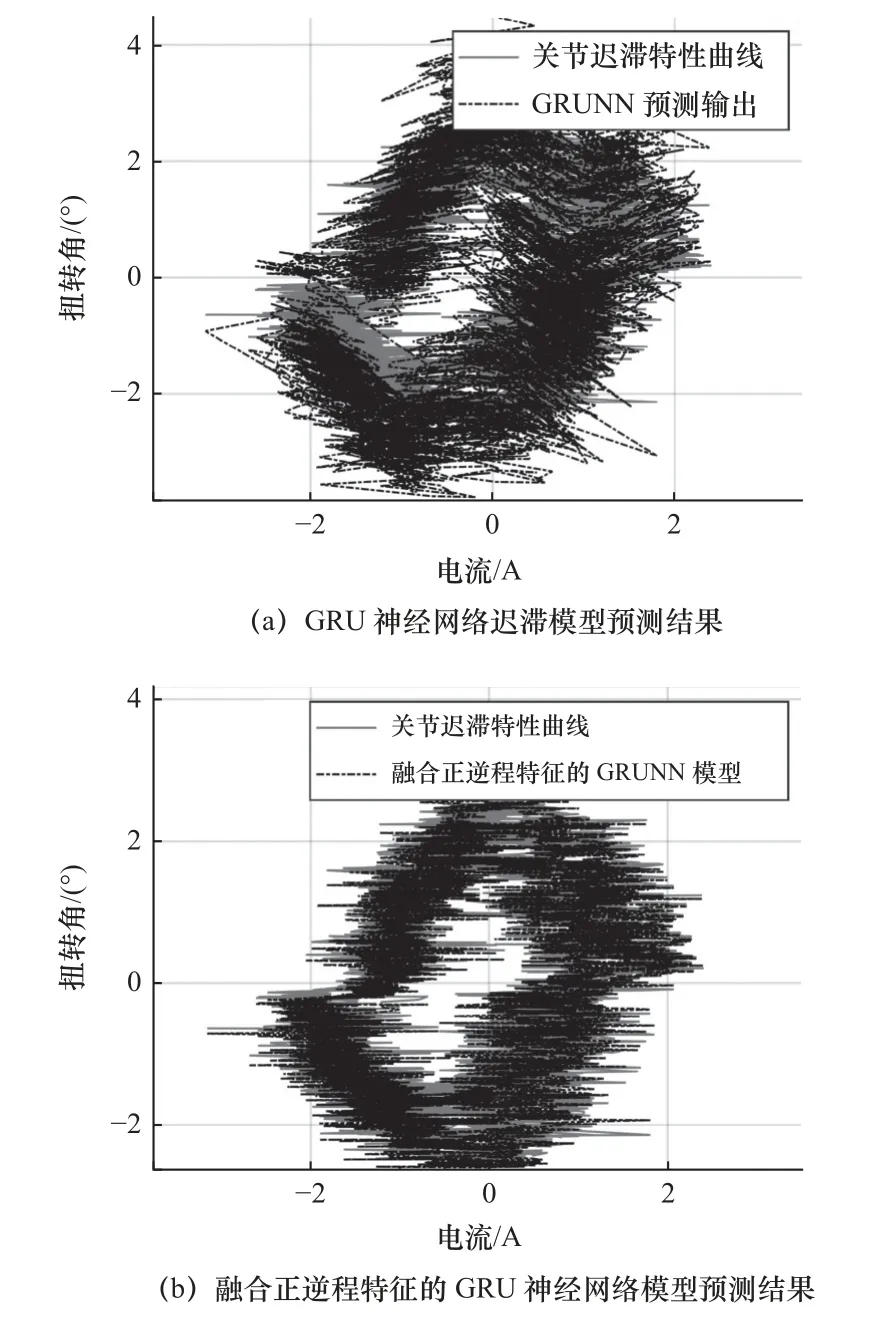
圖16 周期為13 s 的遲滯特性預測結果對比圖

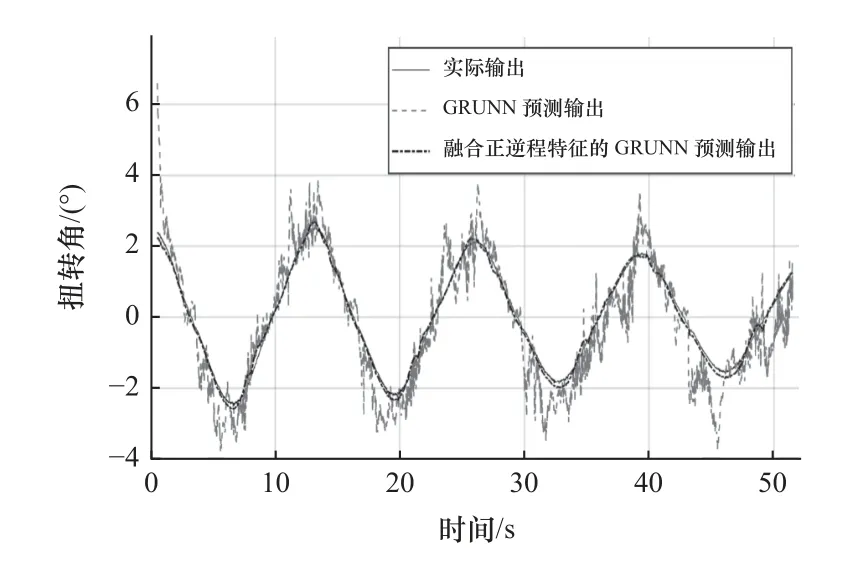
圖17 周期為13 s 的遲滯特性預測輸出時域展開對比圖

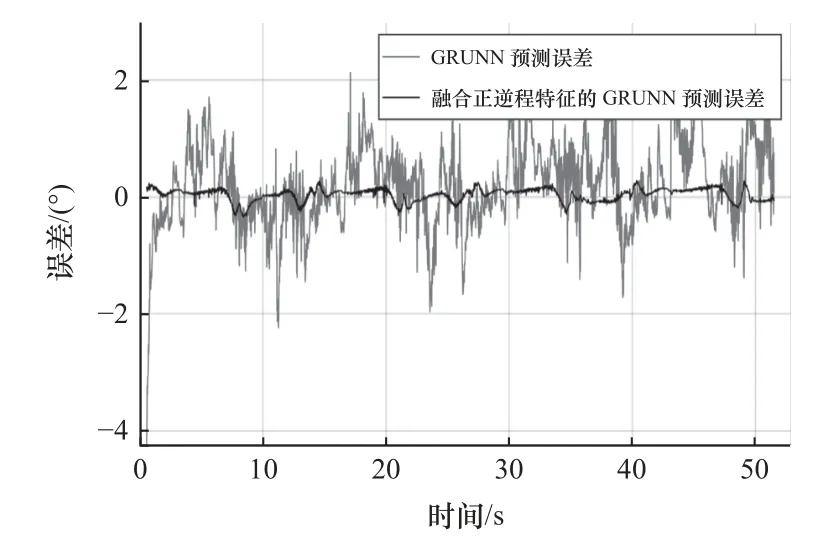
圖18 周期為13 s 的遲滯特性預測誤差對比圖

3.3 實驗結果比較分析

表1 為GRU 神經網絡遲滯模型和融合正、逆程特征的GRU 神經網絡遲滯模型對機器人柔性關節在正弦衰減的運動軌跡下產生的遲滯特性的預測結果。使用均方誤差評估模型的預測結果之外，考慮到模型的進一步應用更關注預測結果的最大誤差。所以，表1 使用均方誤差和最大誤差兩個指標對所構建的關節遲滯模型進行綜合預測結果對比。

表1 兩種模型對正弦衰減信號產生的遲滯特性的預測結果

由表1 可得，融合正、逆程特征的GRU 神經網絡遲滯模型對不同周期下的遲滯特性的預測輸出比GRU 神經網絡的預測輸出的精度有較大提升，其中均方誤差平均減少了98.1%，表明正、逆程特征對GRU 神經網絡在不同周期信號激勵下的遲滯特性建模起到了重要作用。融合正、逆程特征的GRU 神經網絡遲滯模型預測輸出的最大誤差在不同周期下均有下降，隨著周期的增加誤差減小明顯。根據上述實驗結果可得，與GRU 神經網絡遲滯模型的預測結果相比，融合正、逆程特征的GRU 神經網絡遲滯模型可以有效描述不同周期下的柔性關節遲滯特性，具有更好的預測精度。

4 結語

本文針對低成本輕型工業機器人柔性關節未配置負載轉矩傳感器特點以及往復運動時表現出的遲滯特性，根據機器人關節執行器所提供的有限信息，與輸出轉矩-扭轉角之間關節遲滯特性建模方法不同，采用電機驅動電流-扭轉角之間的關系描述柔性關節遲滯特性，提出了一種融合正、逆程特征的GRU 神經網絡遲滯模型。其中：①將輸入電流信號進行卡爾曼濾波，濾除高斯白噪聲的干擾，并將濾波后的信號再次通過卡爾曼濾波以得到合適的電流增量特征；通過卡爾曼濾波去除計算電流增量帶來的高頻噪聲，得到可以反映遲滯特性正、逆程變化趨勢的特征信號；使用模型預測輸出的歷史信息作為神經網絡的輸入信號構建動態的GRU神經網絡遲滯模型，利用GRU 的記憶能力和非線性映射能力對遲滯特性進行建模。在搭建的GLUON 機器人實驗平臺，對柔性關節在不同頻率下的遲滯特性進行預測。實驗結果表明，與GRU神經網絡遲滯模型相比，本文所提出的融合正、逆程特征的GRU 神經網絡遲滯模型能夠有效描述不同周期信號激勵下的輕型工業機器人柔性關節遲滯特性。