初中數學競賽中圖形旋轉變換問題探微

作者簡介：李軍（1988～），男，漢族，安徽無為人，江蘇省南京市南京師范大學附屬中學樹人學校，研究方向：競賽數學、中高考志愿填報機制。

摘 要：圖形旋轉變換問題是初中數學競賽中的一種常見題型。對學生而言，此類題型也是數學競賽中的一個難點。觀察能力欠佳、生活經驗不足、解題思路較窄是導致圖形旋轉變換問題教學效益低的重要因素。鑒于此，教師應采取創設情景、聯系生活、變式訓練等策略，循序漸進、有的放矢地提升圖形旋轉變換問題的教學效益，促進學生邏輯推理、數學抽象、直觀想象等核心素養的全面發展。

關鍵詞：初中數學競賽；圖形旋轉變換；問題探微

中圖分類號：G633.6 文獻標識碼：A 文章編號：1673-8918（2023）47-0064-04

以賽促學是發展學生數學核心素養、提升數學教學效益的一條有效途徑。數學競賽能夠較為全面、客觀、準確地檢測學生的數學核心素養，能夠挖掘學生的數學潛能，調動學生學習數學的積極性。圖形旋轉變換是初中數學競賽中的一種常見題型，也是一個教學難點。鑒于此，教師應通過細致了解圖形旋轉變換問題的教學意義，透徹分析圖形旋轉變換問題的教學困境，深入探究圖形旋轉變換問題的教學策略，著力提升圖形旋轉變換問題的教學效益。

一、圖形旋轉變換問題教學意義分析

邏輯推理能力、直觀想象能力和數學抽象能力等，都是初中數學教學中發展學生核心素養的基本內容。“圖形的旋轉”是蘇科版八年級數學下冊中的內容。在解決圖形旋轉變換問題時，學生需要進行邏輯推理、直觀想象以及數學抽象等，因此，圖形旋轉變換問題有助于培養學生的邏輯推理能力、直觀想象能力和數學抽象能力等。

（一）有助于培養學生的邏輯推理能力

邏輯推理是指根據已有事實，或已知命題，遵循邏輯規則推理出一個新命題的思維過程。在解決圖形旋轉變換問題時，學生需要根據已知條件（已有事實），以及與圖形旋轉變換相關的已知命題，層層深入推導、推理出未知條件。在此過程中，學生的邏輯推理能力也會逐步發展。

旋轉的概念、旋轉三要素（旋轉中心、旋轉方向和旋轉角）、旋轉形成的條件（一個中心、一個方向和一個角度）、旋轉的性質等，都屬于已有事實，都是學生解決圖形旋轉變換問題的主要依據。為了能夠有序、有效解決與圖形旋轉變換相關的數學問題，學生必須要深度理解、熟練掌握、靈活運用這些數學知識。在解決不同類型的圖形旋轉變換問題時，學生需要運用關于圖形旋轉的不同概念。如：當學生在判斷“國旗上升、足球滾動、風車旋轉”等生活現象是否屬于旋轉時，需要根據旋轉的概念、旋轉的三要素這些已知事實、已知命題，進行邏輯推理。

以解決圖形旋轉變換問題為契機，學生不僅能夠更進一步地理解與圖形旋轉變換相關的數學概念，而且能夠循序漸進地發展自身的邏輯推理能力。隨著學生邏輯推理能力的提升，他們解決各種數學問題的能力也會得到提升。

（二）有助于培養學生的直觀想象能力

直觀想象是指借助于幾何直觀和空間想象能力，感知事物形態、物象變化的一個過程，也是學生以圖形為支架，分析、解決問題的一個過程。通過啟迪、指導學生有效解決圖形旋轉變換問題，能夠促進學生直觀想象能力的發展，進而提升學生解決數學問題的能力。

例如，在引領學生解決圖形旋轉變換問題時，為了降低學生解決問題的難度，提升學生解決問題的效度，教師需要利用信息技術手段，聯系實際生活，創設形象生動的教學情境；教師也需要利用一些實物教具，讓學生直觀感知、細致探究圖形變換規律等。無論是教師利用信息技術手段創設的教學情境，還是教師利用實物教具創建的學習場域，都能夠將抽象、復雜、枯燥、低效的圖形旋轉變換問題形象化、簡單化、趣味化、高效化。尤為重要的是，通過探究、分析、解決圖形旋轉變換問題，學生的直觀想象能力能夠得到發展與提升。

在教師的指導下，學生通過依托教學情境、借助實物教具有效解決圖形旋轉變換問題，能夠更為清晰、準確、真切地感知圖形旋轉變換規律，能夠逐步形成直觀想象能力，進而促進學生數學核心素養全面發展。

（三）有助于培養學生的數學抽象能力

從數量與數量關系、圖形與圖形關系之中，抽絲剝繭抽象、概括、總結出數學概念的過程，是發展學生數學抽象能力的一個過程。圖形旋轉變換問題重在研究圖形旋轉之前與旋轉之后、圖形旋轉與圖形靜止之間的關系。因此，圖形旋轉變換問題有助于培養學生的數學抽象能力。

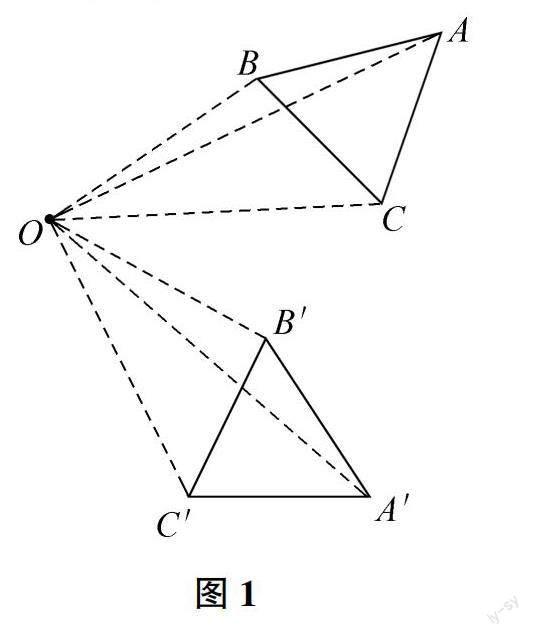
例如，在引領學生探究圖形旋轉的概念時，教師借助板書（如圖1）向學生展示了△ABC旋轉的過程。通過觀察教師的板演，學生發現：△ABC在旋轉過程中，始終圍繞O點；在旋轉一定的角度之后，△ABC到達了一個新的位置，且從原來的視角觀察時，該三角形的形態也發生了一些變化，即△A′B′C′，但實際上，△ABC的形狀與大小并沒有發生改變，只是改變了圖形在平面中的位置。根據△ABC在平面中旋轉的全過程，學生能夠抽象、概括出圖形旋轉的概念。

從上面的案例可以看出，通過思考、分析、解決圖形旋轉變換問題，學生不僅能夠形象直觀地觀察圖形旋轉變換的過程，而且能夠概括、提煉出圖形旋轉的抽象概念。而這，也有助于促進學生數學抽象思維能力的發展。

二、圖形旋轉變換問題教學困境分析

找準圖形旋轉變換問題教學的現實困境，是實施圖形旋轉變換問題教學的切入點。從多年輔導學生參加數學競賽的經歷來看，圖形旋轉變換問題教學所面臨的困境主要包括以下三個方面。

（一）觀察能力欠佳

細致、準確地進行觀察是學生解決圖形旋轉變換問題的基本方法。但是，因為學生觀察能力欠佳，所以無法細致入微、準確無誤地觀察圖形旋轉變換的過程，導致他們找不到解決問題的切入點，進而影響解決問題的效果。觀察的角度、方法等，是影響觀察能力的關鍵因素。

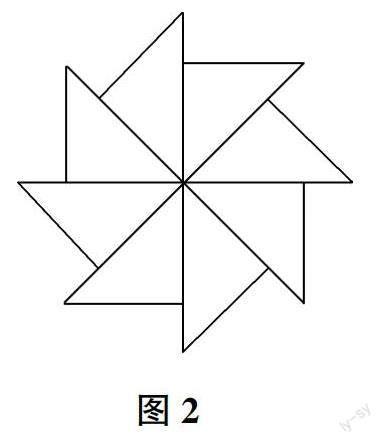
例如，一個三角形經過多次旋轉之后，形成了一個新的圖形（如圖2），問：這個圖形是該三角形旋轉多少次而形成的？每次都旋轉了多少度？在解決這兩個圖形旋轉變換問題時，學生需要仔細觀察圖2，然而，因為學生的觀察能力參差不齊，所以他們的觀察結果也千差萬別。學生甲說：新圖形是原三角形旋轉10次形成的，每次旋轉了36度。學生乙說：新圖形是原三角形旋轉8次形成的，每次旋轉了45度。學生丙說：新圖形是原三角形旋轉7次形成的，每次旋轉了45度……顯然，學生甲和學生乙的答案都是錯誤的，只有學生丙的答案是正確的。通過與學生進一步溝通，教師發現：學生甲和學生乙之所以會出現錯誤，主要是因為他們的觀察方法欠妥，觀察能力欠佳。

學生的觀察能力并不是與生俱來的，而是經過后天培養逐步形成的。既然學生觀察能力欠佳，那么，教師就應該立足圖形旋轉變換問題，有的放矢地培養學生的觀察能力。

（二）生活經驗不足

數學與生活之間有著密不可分的聯系。各種圖形旋轉變換題目源于多姿多彩的現實生活場景。但是，因為學生的生活經驗不足，即在現實生活中未曾經歷、體驗過相關的生活場景，所以他們對圖形旋轉變換題目理解不透徹、不準確。此外，生活經驗的不足，也會導致學生無法將圖形旋轉變換與現實生活聯系起來。

例如，有一塊直立在地面上的長方形空心磚ABCD（如圖3），工人師傅將這塊磚輕輕地推倒。在此過程中，空心磚的A點始終保持不變，B、C、D點發生了旋轉，分別旋轉到了B′、C′和D′，構成了一個新的長方形AB′C′D′，問：該空心磚旋轉過程中的旋轉中心在哪？該空心磚旋轉了多大角度？因為學生在實際生活中未曾有過在地面上旋轉空心磚的經歷，所以他們對該生活場景比較陌生。相關生活經驗的缺乏，也成為學生解答這道題目的主要障礙。

在解答圖形旋轉變換題目時，如果學生生活經驗不足，那么，他們就無法基于已有生活經驗解決相關問題。因此，根據圖形旋轉變換的過程，聯系實際生活，創設相關的情景，也就成為教師豐富學生生活經驗的有效路徑。

（三）解題思路較窄

同樣的問題，往往可以從不同的角度予以解決。此舉能夠拓展學生的解題思路、提升學生的解題能力。聚焦學生解決圖形旋轉變換問題的過程，可以發現：解題思路較窄是圖形旋轉變換問題教學所面臨的現實困境之一。窄化的解題思路，禁錮了學生的解題思維，降低了學生的解題效果。

例如，在解答一些圖形旋轉變換問題時，因為學生循規蹈矩、思維僵化，所以解題步驟煩瑣、解題過程復雜、解題錯誤頻出。同時，學生創新思維的發展也會受阻。學生之所以循規蹈矩、思維僵化，一方面，是因為教師在指導學生解答圖形旋轉變換題目時，未能有序、有趣、有效地開展變式訓練，未能有針對性地拓展學生的思維和解題思路；另一方面，是因為學生缺乏創造性解決問題的意識、能力，教師未能通過啟迪、點撥、評價喚醒學生的創新意識、點燃學生的創新激情等。

窄化的解題思路不僅會影響學生的解題效果，而且會影響學生創新思維的發展。因此，在圖形旋轉變換教學中，適時適當地拓展學生的解題思路，也就成為教師提升教學效益的當務之急。

三、圖形旋轉變換問題教學對策分析

針對圖形旋轉變換問題教學中所面臨的學生觀察能力欠佳、生活經驗不足以及解題思路較窄等現實困境，教師應采取創設情景、聯系生活和變式訓練等策略，培養學生的觀察能力、豐富學生的生活經驗以及拓展學生的解題思路，以此提升圖形旋轉變換問題教學的效益，促進學生直觀想象、數學抽象和邏輯推理等核心素養的全面發展。

（一）創設情景，培養學生的觀察能力

鑒于學生觀察能力欠佳的現實問題，教師可依托信息技術、利用實物學具，創設圖形旋轉變換情景，以此拓展學生的觀察視角，指導學生熟練掌握各種觀察方法，提升他們的觀察能力。

1. 依托信息技術，創設圖形旋轉變換情景

隨著教育信息化時代的到來，信息技術在初中數學教學中的運用越來越廣泛。為了讓學生動態觀察、深入探究圖形旋轉變換的過程、規律等，教師可依托信息技術手段，創設圖形旋轉變換情景。

例如，某學生將一張長方形的白紙ABCD（如圖4）沿GH對折之后，點C落在了點Q處，點D落在了點E處，EQ與BC交于點F，若AD=8cm，AB=6cm，AE=4cm，則△EBF的周長是多少厘米？因為學生受到自身空間想象能力的限制，所以他們無法想象、觀察題目中所描述的問題情景。為此，教師依托信息技術手段，動態展示了該問題情景。與此同時，為了引領學生更為細致地觀察圖形旋轉變換過程，教師還利用信息技術手段，多視角、全方位地進行了展示。

信息技術的巧妙運用，讓學生觀察長方形白紙ABCD沿GH對折過程的視角更廣闊、更細致，原本抽象、復雜的問題情景變得形象、簡單。依托信息技術創設教學情景，能夠降低學生解題的難度，提升學生解題的效度。

2. 利用實物學具，創設圖形旋轉變換情景

為了讓學生理解抽象的圖形旋轉變換過程，教師也可以組織學生利用一些實物學具，自主創設圖形旋轉變換情景。如此，在動手操作、親身體驗的過程中，圖形旋轉變換情景就會變得可視、可觸。

仍然以“某學生將一張長方形的白紙ABCD沿GH對折”的問題情景為例，教師可指導學生拿出一張白紙，并根據題目要求動手折疊。在此過程中，一張貌似微不足道的白紙，就成為學生的實物學具。聚焦真實、有趣的折紙活動，學生能夠直觀、清晰地觀察、了解題目中長方形白紙的旋轉變換過程。而這，也有助于學生找準解決問題的切入點，提升學生解決問題的實效性。

此外，在實際教學中，教師可組織學生根據圖形旋轉變換的問題情景，利用廢舊紙盒、雪糕棒、棉簽棒等低成本物品，制作一些簡易學具。之后，指導學生利用這些實物學具，模擬演示問題情景中圖形旋轉變換的過程，將抽象的問題形象化、復雜的問題簡單化。

（二）聯系生活，豐富學生的生活經驗

豐富的生活經驗是學生解決圖形旋轉變換問題的重要支撐。既然學生關于圖形旋轉變換的生活經驗不足，那么，教師就應該聯系多姿多彩的現實生活，以學習任務、課后作業為媒介，有的放矢地豐富學生的生活經驗。

1. 以學習任務為媒介，聯系現實生活

主題鮮明、內容豐富、形式多元的課堂學習任務是教學目標的一種載體，也是聯系現實生活的一種媒介。通過組織學生完成與現實生活密切相關的學習任務，不僅有助于學生深度理解相關的數學知識，而且有助于豐富學生的生活經驗。

例如，為了讓學生深度理解圖形旋轉的概念、旋轉的三要素等數學知識，教師在課堂中設計了一些有趣的學習任務，包括讓學生利用白紙、彩筆、圖釘、小木棍等制作簡易風車，讓學生利用五顏六色的紙張折疊、制作千紙鶴、小青蛙、小衣服、小褲子等。不僅如此，教師還要求學生根據自己制作簡易風車、折疊各種小物件的過程，梳理、歸納、總結圖形旋轉的概念，以及圖形旋轉的三要素。

在上面的案例中，學習任務成為學生聯系現實生活的一種媒介，成為學生理解抽象數學概念的一扇窗口。在樂此不疲、積極主動地完成上述學習任務的過程中，學生會積累豐富的生活經驗。

2. 以課后作業為媒介，聯系現實生活

課后作業是課堂的延伸、補充，是促進學生核心素養發展的一種推手，也是豐富學生生活經驗的一種渠道。教師應以課后作業為媒介，聯系現實生活，讓學生以完成課后作業為契機，豐富自己的生活經驗。

例如，為了讓學生動態觀察、細致了解三角形的旋轉變換過程，教師設計了一項課后作業，即讓學生自選一些低成本材料，自主制作一些三角形學具，并利用這些學具自己探究相關的圖形旋轉變換的問題情景。學生甲利用吸管制作了幾個大小、邊長等均不同的三角形學具，之后，利用這些三角形學具自主探究了相關的問題情景。學生乙則利用一些細鐵絲制作了幾個大小各異、邊長不等的三角形學具，并利用這些學具自主探究相關的問題情景……

教師以課后作業為媒介，將圖形變換問題情景與多姿多彩的現實生活聯系在一起，不僅能夠讓課后作業的形式變得更加有趣，而且能夠讓學生在完成課后作業的過程中積累豐富的生活經驗。

（三）變式訓練，拓展學生的解題思路

鑒于學生解題思路較窄的現實困境，教師可組織學生在課堂內外有的放矢地開展一些變式訓練，其是課堂教學中不可或缺的一個環節。通過組織學生積極主動、卓有成效地完成變式訓練，能夠更好地拓展學生的解題思路，引領學生更深、更細、更透地理解相關知識。

例如，在課堂中，教師可在引領學生解決三角形旋轉變換題目的基礎上，進一步解決一些正方形旋轉變換、長方形旋轉變換的題目。這些正方形、長方形旋轉變換題目，都是三角形旋轉變換題目的變式訓練。通過解答這些同類型的題目，學生能夠觸類旁通，更為熟練、準確地解答圖形旋轉變換題目。同時，學生的解題思路會更加開闊，解題能力也會穩步提升。

此外，教師在設計課后作業時，也可以設計一些變式訓練題目，要求學生根據圖形旋轉變換的問題情景，自主創編、自主解答一些變式訓練題目。在此基礎上，梳理、歸納解題思路。

四、結論

總而言之，為了提升學生解答圖形旋轉變換問題的能力，發展學生的數學核心素養，教師應深度探究影響圖形旋轉變換問題教學效益的因素，并以此為切入點，采取創設情景、聯系生活和變式訓練等策略，提升圖形旋轉變換問題的教學效益。如此，學生就能夠游刃有余地解答初中數學競賽中的圖形旋轉變換題目。

參考文獻：

［1］莊凌婕.初中數學中圖形變換的相關教學［J］.試題與研究，2020（5）：6-7.

［2］田佩佩.剖析初中數學圖形旋轉問題的幾種方法［J］.數學之友，2022，36（14）：68-70.

［3］吳艷華.關于圖形旋轉變換專題的解題方法探究［J］.數理化解題研究，2021（29）：48，60.

［4］曹華慶.有效情境·實踐操作·人文拓展——與初中數學《圖形的旋轉》遙遙“對話”［J］.數學學習與研究，2021（3）：29-30.