核心素養立意下的函數與導數命題
周建鋒
? 華南師范大學附屬中學
1 命題
原創題已知函數f(x)=ex-1-lnx(其中e=2.718 28……是自然對數的底數),過點(a,b)(a≠0)可作曲線f(x)的兩條切線.
(1)請給出a,b應滿足的充要條件;
考查目標:重點考查學生綜合運用函數和導數解決實際問題的能力,以及對新情境問題分析理解的能力.
設計思路:近幾年全國及各地高考數學卷對極值點偏移問題考查得比較多,廣大師生對這類題的研究比較深入,難以考查出學生的實際能力.2022年全國Ⅰ卷別出心裁,考查交點問題并證明三個交點橫坐標成等差數列,體現出推陳出新的導向.
本題融入切線問題,考查學生對切線問題的分析能力.f(x)是一個下凸函數,過某些平面區域的點可作兩條切線,過某些平面區域的點可作一條切線,過某些平面區域的點沒有切線,這需要學生進行深入分析,并作出嚴謹的論述.得到a,b應滿足的充要條件后,第(2)問設計了一個不等式,需要利用第(1)問的結論,將不等式進行優化,而且優化后直接證明也有難度,需要用放縮或分析隱零點等手段進一步證明.
2 命題過程
原始題已知函數f(x)=ex-1-lnx(其中e=2.718 28……是自然對數的底數).
(1)求f(x)的最小值;
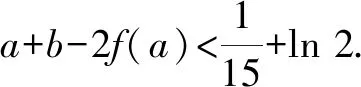
(參考數據:ln 2≈0.693 1,ln 3≈1.098 6,ln 5≈1.609 4.)
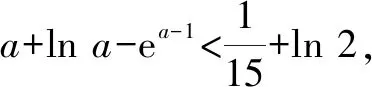
修改1已知函數f(x)=ex-1-lnx(其中e=2.718 28……是自然對數的底數).
(1)求f(x)的最小值;
(2)若過點(a,b)(a≠0)可作曲線f(x)的兩條切線,求證:b<2f(a)-a2+2a-1.
(參考數據:ln 2≈0.693 1,ln 3≈1.098 6,ln 5≈1.609 4.)
說明:通過這次修改,第(2)問需要證明一個復雜的不等式ex-1-lnx-x2+2x-1>0,但可以通過第(1)問的結論,放縮為-x2+2x>0在0
修改2已知函數f(x)=ex-1-lnx(其中e=2.718 28……是自然對數的底數).
(1)求f(x)的最小值;
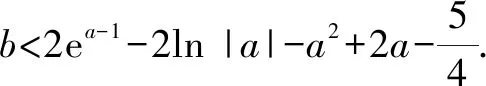
(參考數據:ln 2≈0.693 1,ln 3≈1.098 6,ln 5≈1.609 4.)
說明:解決了修改2的兩個問題后,題目已經比較完善了,但又覺得第(1)問與第(2)問沒有關聯性,顯得別扭(僅僅為了給學生送幾分而已),故修改為刪去第(1)問,把第(2)問分割成兩個問題.
修改3已知函數f(x)=ex-1-lnx(其中e=2.718 28……是自然對數的底數),過點(a,b)(a≠0)可作曲線f(x)的兩條切線.
(1)請給出a,b應滿足的充要條件;
(參考數據:ln 2≈0.693 1,ln 3≈1.098 6,ln 5≈1.609 4.)
說明:到第四稿,還是覺得第(2)問的結構不是很完美,證明過程中過多地用到一些特殊數據,所以再次修改,得到最終稿,即本文開頭的原創題.
3 試題分析
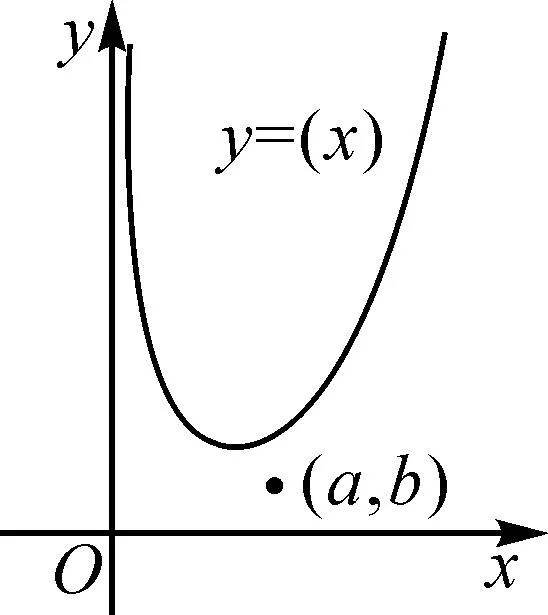
圖1
解答第(1)(2)問的思維導圖如圖 2、圖3所示.

圖2 第(1)問思維導圖

圖3 第(2)問思維導圖
4 實測結果
本題為2023屆某市四校聯考壓軸題,滿分12分.我校本題平均分3.07,難度0.26,區分度0.21.由于整套試卷題目偏難,導致能做到本題的學生比較少.學生出現的問題主要有如下幾個方面:
(1)運算能力不過關
②忽略了定義域(0,+∞)對函數性質的影響.
(2)論證不嚴謹
使用“易得a>0,b (3)轉化能力不足 在第(2)問中,少數學生沒有考慮用第(1)問的條件進行放縮,而是用切線方程將b替換成以兩個切點x1,x2為元的不等式,難以證明. 通過幾次修改,筆者對題目的構思角度、結構設計、考查素養等方面頗為滿意.首先,對函數曲線切線的分析是一個比較新穎的角度,通過對切線條數的分析,將問題轉化為方程解的個數問題,也即函數交點問題,與導數完美結合.其次,利用a,b滿足的條件證明一個雙變量不等式,通過第(1)問的條件進行放縮,消去b,轉化為關于a的不等式的證明.要證明指對數混合的不等式,需要扎實的化歸轉化基礎,對學生的應變能力是一個很大的考驗.Z5 體會

