穩態性能下T型槽柱面氣膜密封結構參數非線性回歸分析*

熊忠汾 劉美紅 韋邱發 李 鑫

(昆明理工大學機電工程學院 云南昆明 650504)

氣膜密封技術能夠利用氣體介質的動壓效應，在密封界面間形成微米級的氣膜，從而使得密封界面保持非接觸的密封方式。氣膜密封能夠在降低泄漏量的同時，減少動、浮環密封界面磨損，提高密封系統在高速透平機械中的可靠性與長周期壽命，因而在高速流體機械中，氣膜密封是一種非常有效的密封方式，并成為密封研究中的熱點[1-3]。

在氣膜密封中，端面密封技術被研究人員廣泛研究并得以應用。但在航空發動機轉子系統中，由于工作環境影響而產生的位移形變以及轉子存在著較大的徑向跳動[4]，使得端面密封技術受到限制。而柱面氣膜密封由于具有較大的柔性，能夠適應轉子的徑向位移[5-7]，成為一種重要的密封形式。T型槽柱面氣膜密封因其結構特性，能夠適應轉子雙向旋轉，并且有著優異的密封性能，成為研究人員的重點研究對象之一。

胡文績、李濤子等[8-9]使用Fluent進行仿真試驗，研究了T型槽干氣密封的穩態性能，同時也驗證了使用數值模擬方法的可行性。王衍等人[10]針對改良T型槽槽型結構參數，使用數值模擬的方法研究了開啟力的變化規律。彭旭東、蘇澤輝等[11-13]在不同工況條件下分析了T型槽穩態性能的變化情況，發現槽長壩長比等結構參數對氣膜剛度和泄漏率有著較大的影響。然而，目前關于各因素對T型槽穩態性能影響程度的分析判斷的文獻還很少見。因此，本文作者研究了結構參數的變化及其關聯特征對T型槽柱面氣膜密封穩態性能的影響，比較了各結構參數的影響程度，為實際工程應用提供參考。

1 數值計算模型

1.1 T型槽柱面氣膜密封系統工作參數

表1給出了密封氣膜系統完整的結構參數。根據表1給出的結構參數，使用Creo三維輔助設計軟件完成對柱面氣膜密封系統的建模。T型槽柱面氣膜密封結構簡圖如圖1(a)所示，圖1(b)示出了單個槽型的平面幾何尺寸。其中l為氣膜軸向長度，w1和wq分別是T型槽窄槽寬度和寬槽寬度，wr為非槽區平臺寬度，βr和βg分別是寬槽長度和窄槽長度。

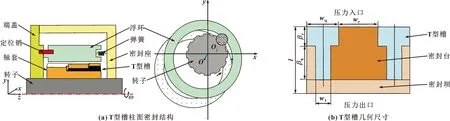
圖1 T型槽柱面密封結構及幾何尺寸

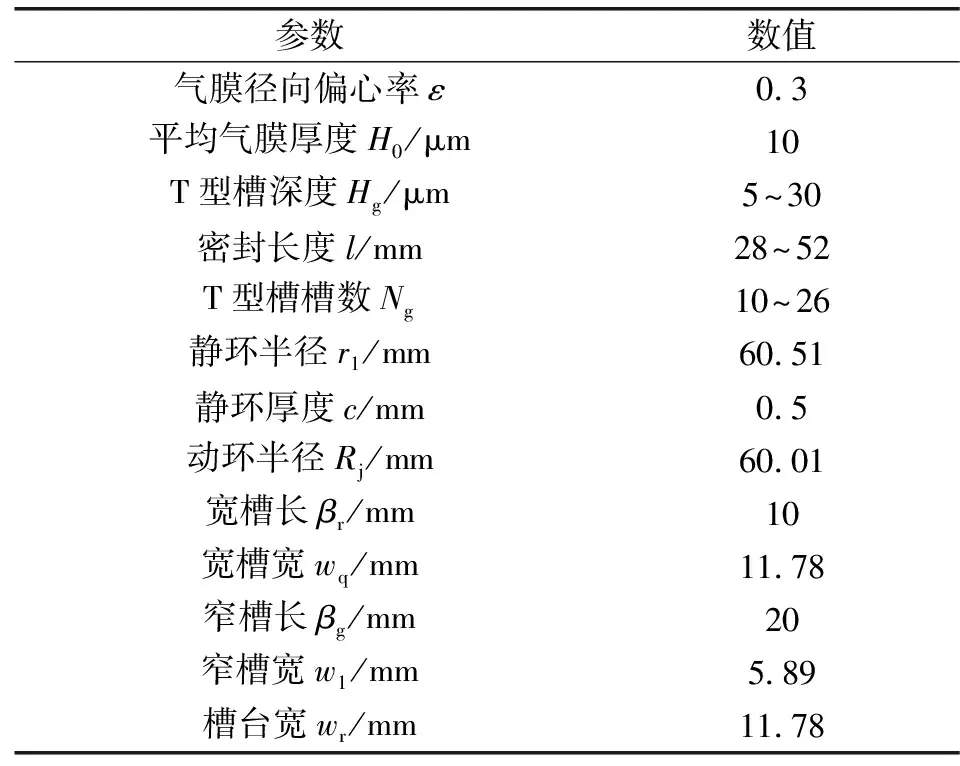
表1 T型槽柱面氣膜密封系統結構參數

1.2 材料屬性

參考文獻[14]的研究成果，選擇密封環的材料和對應屬性如表2所示。

表2 動靜環材料屬性

進行數值模擬求解時設置密封流體為空氣，其密度為1.29 kg/m3，動力黏度為1.48×10-5Pa·s。

1.3 網格劃分

由于氣膜厚度是微米級，文中利用有限元前處理軟件ANSA強大的網格劃分功能，在徑向方向上將氣膜共分成6層，并生成六面體結構性網格，隨后進行網格獨立性檢驗。為提升計算效率，確定網格數量為126萬個結構性體網格。圖2所示分別為網格整體和氣膜厚度分層放大圖。

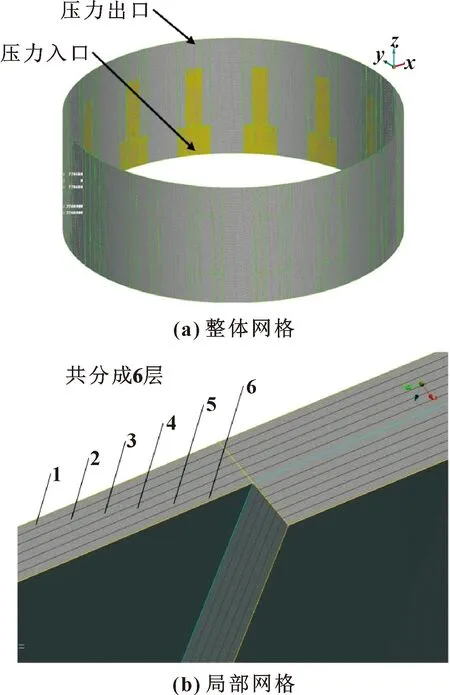
圖2 氣膜網格劃分示意

1.4 邊界條件設置

如圖2(a)所示，文中選擇T型槽寬槽處為壓力入口，氣膜壩區徑向截面設置為壓力出口，并設定出口壓力為一個標準大氣壓，進出口壓力差大小為0.1 MPa；無槽浮環設置為無滑移速度邊界，有槽動環設置為旋轉動態壁面，其轉速大小為43.5 m/s。

1.5 流體運動狀態判定

計算模擬引入如下假設：

(1)不考慮系統內流體的體積力和慣性力的作用。

(2)假定密封系統內與壁面接觸的流體能保持壁面相同的速度，即不存在相對滑移速度。

(3)柱面氣膜密封系統內氣體介質符合牛頓黏性定律。

(4)不考慮動浮環所產生的微小形變。

密封系統內軸向方向流體的流動方式為Poiseuille流，周向方向的流體為Couette剪切流，其雷諾數的計算方法分別如公式(1)、(2)所示。

Poiseuille流動的雷諾數：

(1)

Couette剪切流動雷諾數：

(2)

式中：ρ為工作流體密度；h為特征尺寸，文中選擇其為氣膜膜厚；μ為流體動力黏度；vc和vz分別為周向和軸向速度。

其中軸向速度大小的計算公式使用王學良等[15]推導出的公式(3)。

(3)

由于實際工作中密封內流體在轉速和壓力的共同影響下，流體流動方式較為復雜，為判斷流體流動方式，使用BRUNETIRE等[16]提出的判斷方法：

(4)

當流動因子a>1時，則認為系統內流體流動狀態為紊流；當α<0.562 5時，則認為系統內流體流動狀態為層流。

使用前文所給出的相關參數，計算得到文中Rep和Rec分別為4.05和31.3。根據式(4)計算得α=0.020 07<0.562 5，因此文中流體運動狀態為層流。

2 氣膜流場數值分析與討論

2.1 穩態性能計算方法

(1)平均氣膜厚度

H0=(hmax+hmin)/2

(5)

式中：hmax指氣膜厚度最大處的值；hmin指氣膜厚度最小處的值。

(2)泄漏率

(6)

式中：Q代表泄漏率；Rj表示動環半徑；p指氣膜工作壓力；θ是最大膜厚處的角向坐標。

(3)浮升力

(7)

式中：Ft為氣膜周向切線方向分力；Fr為浮環徑向分力；Fg為浮升力合力。

(4)氣膜剛度

(8)

式中：F表示浮升力。

2.2 計算模型驗證

為驗證所建立的數值計算模型的準確性，在與文獻[17]相同的參數設置下，研究氣膜密封系統泄漏率隨轉速改變的情況，并與文獻結果進行了對比，如圖3所示。可以看出，文中模型的計算結果與文獻得到的泄漏率變化情況一致，并且符合程度較高，驗證了文中模型的正確性。

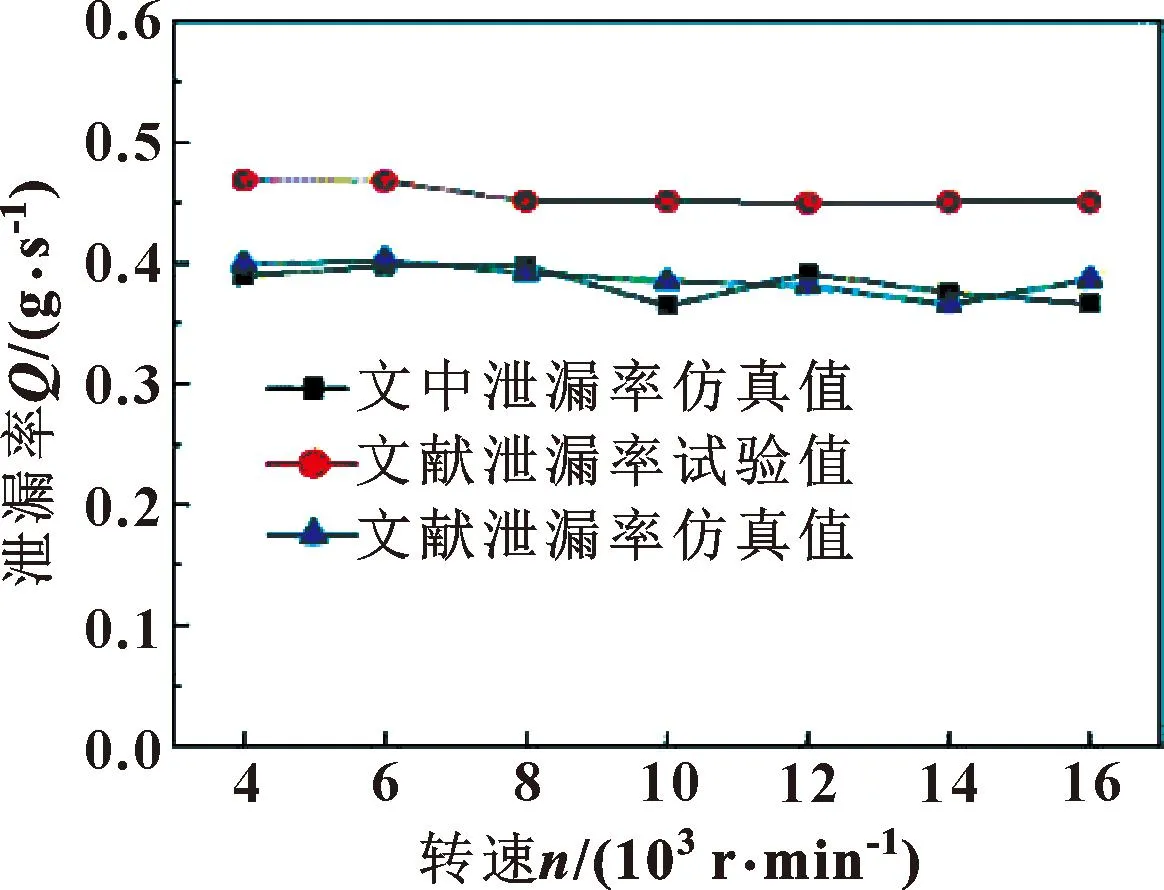
圖3 不同轉速下泄漏率比較

2.3 結構參數對泄漏率的影響

圖4所示是轉速8 000 r/min下，分別改變密封長度、T型槽槽數和槽深等結構參數，系統泄漏率的變化情況。可知，隨著3種結構參數的增大，系統泄漏率整體變化并不明顯。從圖4(a)可看出，增大密封長度系統泄漏率呈現逐漸降低的趨勢，但下降梯度非常緩慢，密封長度從28 mm到52 mm增大24 mm，而泄漏率下降值僅為7.5 mg/s。泄漏率下降是由于密封長度的增加會使得通道內流體行程增加，從而損失更多的能量。但相較于流體本身具有的動能，通道增長損失的能量很少，因此泄漏率下降的趨勢并不明顯。從圖4(b)、(c)可知，增大T型槽槽數和槽深，系統泄漏率呈現上升趨勢。在圖4(b)中，T型槽槽數由10個增加至26個，泄漏率增加6 mg/s；在圖4(c)中槽深度從5 μm到30 μm增大6倍，而泄漏率增加值為8 mg/s。這是由于柱面密封主泄漏存在于T型槽和浮環之間的區域，增加槽數和槽深會使得通道面積和數量增大，泄漏率隨之提升。

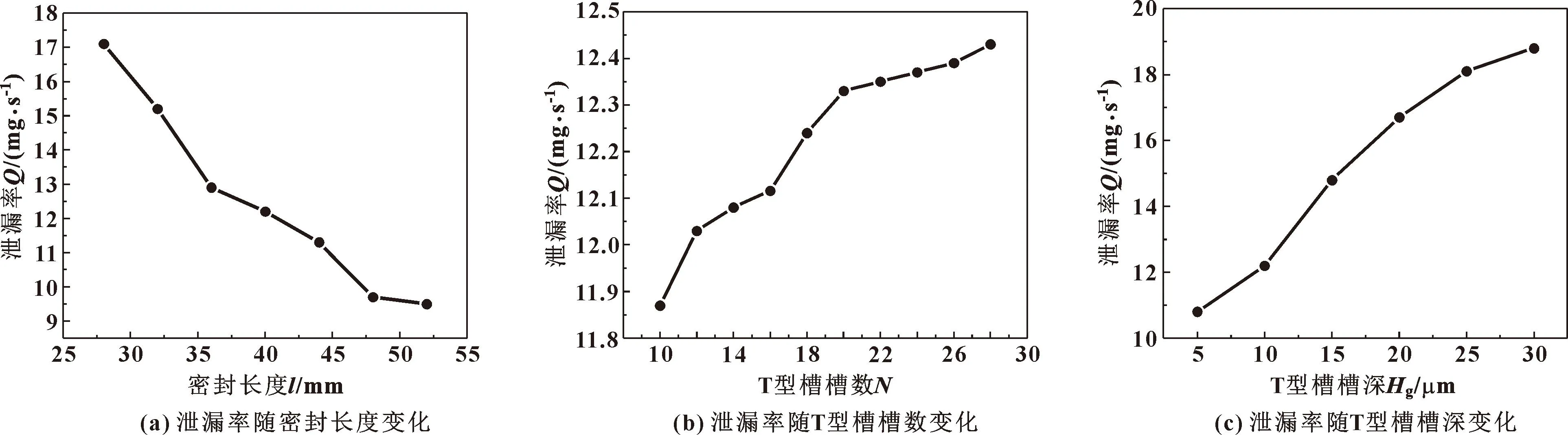
圖4 結構參數對系統泄漏率的影響

2.4 結構參數對浮升力的影響

圖5所示是轉速8 000 r/min下，分別改變密封長度、T型槽槽數和槽深等結構參數，系統浮升力的變化情況。從圖5(a)可以看出，系統浮升力大小隨密封長度變化明顯，密封長度從28 mm到52 mm增大24 mm，浮升力增加值為1 450 N，這是由于增加密封長度會增大通道面積，使得流體動壓效應加強，從而導致浮升力上升。從圖5(b)可知，隨著T型槽槽數的增大浮升力逐漸上升，但趨勢緩慢，T型槽槽數從10到26增加16個，系統浮升力增加值為13 N，說明T型槽槽數對系統浮升力的影響并不顯著。這是因為T型槽槽數增加會使通道流體內壓力加強，浮升力隨之增大，但壓力的增加較少，因此浮升力增大數值也不明顯。從圖5(c)可知，T型槽槽深從5 μm到30 μm增大6倍，系統浮升力增加值為290 N，可見槽深對系統浮升力有較大影響。這是因為T型槽槽深的增加會使得通道內流體動力潤滑效應加強，使得槽型流體泵送能力加強，壓力增大的同時浮升力隨之增加。

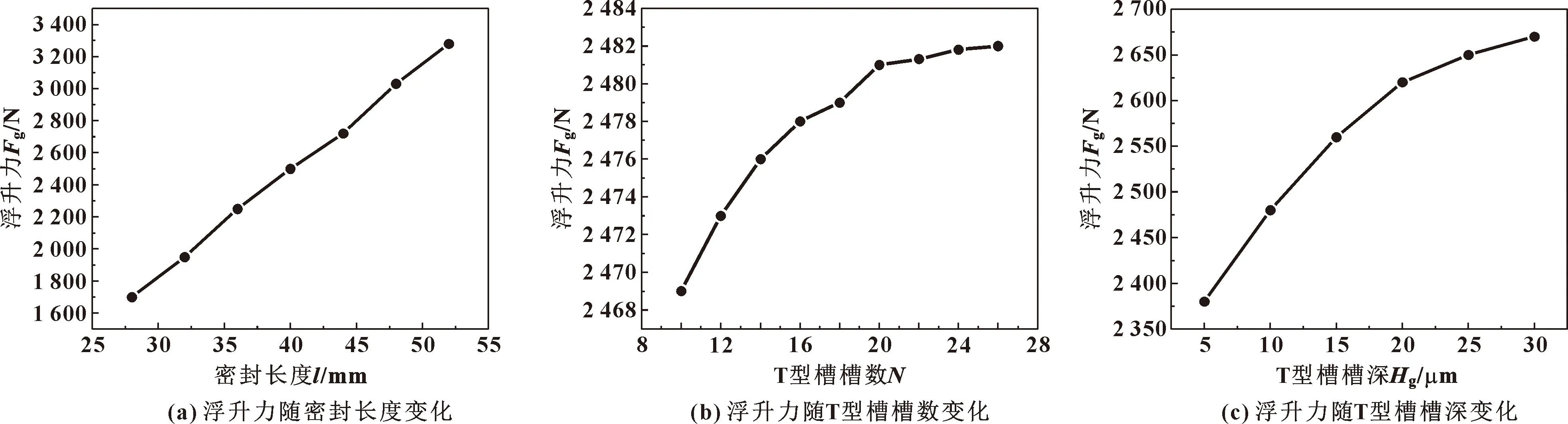
圖5 結構參數對浮升力的影響

2.5 結構參數對氣膜剛度的影響

圖5所示是轉速8 000 r/min下，分別改變密封長度、T型槽槽數和T型槽槽深等結構參數，氣膜剛度的變化情況。從圖6(a)可知，隨著密封長度的增加，氣膜剛度會隨之緩慢增大，這是由于密封長度增加，密封流體動壓潤滑區域面積增大，氣膜剛度得到提升。從圖6(b)可知，T型槽數量從10到26增加16個，氣膜剛度增大1.7×105N/m，這是由于槽數的增加，氣膜動壓效應增強使得氣膜剛度增大。從圖6(c)可以看出，隨著T型槽深度的增加氣膜剛度呈線性增長，T型槽深度從5 μm到30 μm增大6倍，氣膜剛度增值為5.5×105N/m，可見T型槽槽深對氣膜剛度有較大的影響。這是因為槽深的增加，槽內存在氣體更多，流體動壓效應加強，氣膜剛度得到加強。

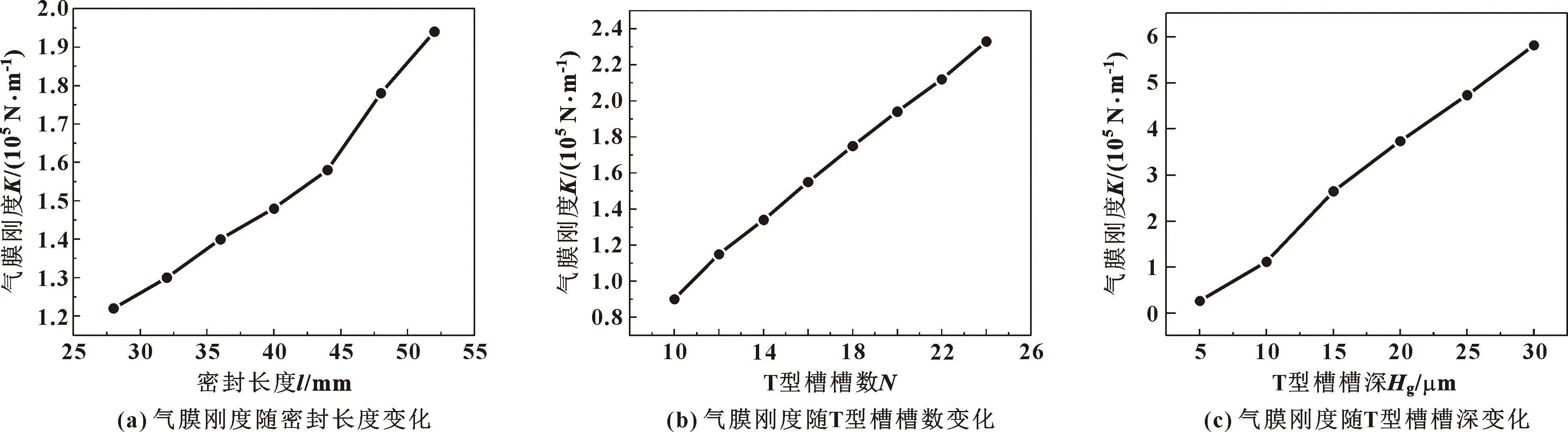
圖6 結構參數對氣膜剛度的影響

2.6 穩態性能多元非線性回歸分析

在定工況下改變單一結構參數，使用多元非線性回歸方程擬合結構參數與穩態性能之間的關系能夠更直觀地實現對穩態性能的預測。

2.6.1 公式擬合

根據數值計算結果，將穩態性能和結構參數表示成公式(9)所示的非線性組合形式：

(9)

式中：x1、x2、x3作為自變量分別代指T型槽槽深、T型槽槽數、密封長度；y為作為因變量的泄漏率、浮升力、氣膜剛度；c0～c3為可變常數。

擬合得到的泄漏率與結構參數的函數表達式為

(10)

擬合得到的浮升力與結構參數的函數表達式為

(11)

擬合得到的氣膜剛度與結構參數的函數表達式為

(12)

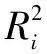
2.6.2 結構參數對密封性能影響程度判斷

為得到各結構參數對穩態性能影響程度的主次順序，采用計算偏回歸系數的方法來判斷，結構參數所對應的偏回歸系數越大表明其影響越大。

偏回歸系數Fj計算公式：

(13)

式中：Sj為偏回歸平方和；Se為均方差。

(14)

(15)

其中Sa為和方差。將式(14)和(15)代入式(13)中，可得

(16)

其中

(17)

為方便計算對公式(10)左右兩邊取對數，并令lny1=Y1，lnx1=X1，lnx2=X2，lnx3=X3得到：

Y1=-8.877 5+0.387 61X1+0.040 92X2-

0.931 77X3

(18)

同理對公式(11)、(12)進行計算，得到各影響因素的偏回歸系數Fj如表3所示。

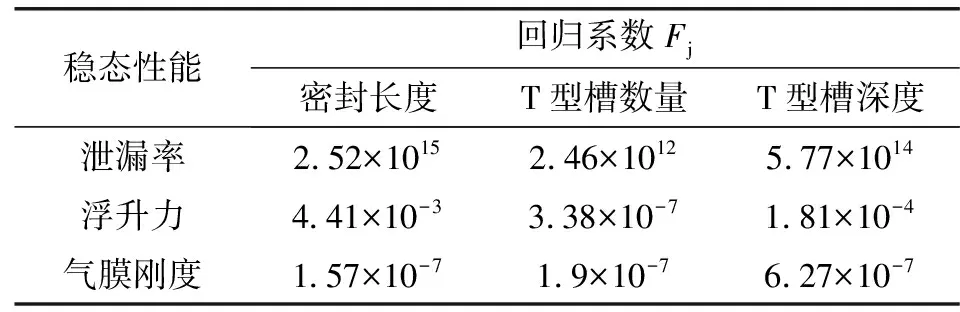
表3 各結構參數的偏回歸系數

根據表1可知，密封長度對泄漏率影響最大，其次是T型槽深度，T型槽數量的影響最弱，因此為了降低系統泄漏率應優先考慮降低密封長度；密封長度對浮升力影響最大，其次是T型槽深度，T型槽數量的影響最弱，與前文仿真試驗結果一致；T型槽深度對氣膜剛度影響最大，其次是T型槽數量，密封長度的影響最弱，與圖6所示的變化趨勢相符。

3 結論

使用數值模擬的方法，研究了轉速為8 000 r/min的工況條件下，結構參數對T型槽柱面氣膜密封穩態性能的影響，并使用多元非線性回歸分析擬合了穩態性能和結構參數之間的關系，判斷出各結構參數對穩態性能影響程度的大小。主要結論如下：

(1)系統泄漏率隨著密封長度增加而減小，T型槽數量和槽深的增加會使得泄漏率下降。影響系統泄漏率最大的因素為密封長度，其次是T型槽深度，T型槽數量影響最小。

(2)浮升力隨著密封長度、T型槽數量和槽深的增加均呈現逐漸上升的趨勢，其中影響最大的是密封長度，其次是T型槽深度，T型槽數量影響最小。

(3)氣膜剛度隨著密封長度、T型槽數量和槽深的增加均呈現逐漸上升的趨勢，其中影響最大的是T型槽深度，其次是T型槽數量，密封長度影響最小。