基于BEM與CFD數值模擬的風力機葉片氣動性能分析

史先路，趙 凡，趙 凱，，趙軍華，3

(1.江南大學 機械工程學院，江蘇 無錫 214122；2.中國空氣動力研究與發展中心，四川 綿陽 621000；3.江蘇省食品先進制造裝備技術重點實驗室，江蘇 無錫 214122）

0 引言

風力機常年運行在惡劣環境下，葉片表面易表現出流動分離、失速等非定常氣動特性，設計新一代高效、輕量化的風力渦輪機，需要更準確地預測氣動載荷。

作為風力機葉片設計及其氣動性能評估的常用方法，葉素動量理論(BEM）[1]由于其計算簡單，能快速預測葉片氣動性能而備受青睞。文獻[2]利用BEM理論分析了風力機葉片氣動載荷的分布規律以及風速大小對葉片氣動載荷特性的影響。作為一種常用的數值模擬方法，計算流體動力學(CFD）可用于解決所有常見的流動問題。文獻[3]，[4]利用CFD方法在均勻來流條件下對風力機葉片表面流動分離情況進行了研究，但未考慮大氣邊界層的影響。文獻[5]基于CFD計算方法研究了一種小型風力機的氣動特性，將計算結果與基于BEM計算方法得到的結果進行了對比，結果表明，兩種計算方法得到的氣動載荷特性相似。文獻[6]基于BEM與CFD計算方法研究了風力機的功率和載荷特性，采用Spalart-Allmaras湍流模型針對海上變速變槳風力機分析了不同雷諾數下兩種計算方法的結果差異，但未考慮失速狀態下葉片表面的流動分離對計算結果的影響。

研究人員利用BEM及CFD數值模擬方法對風力機葉片的氣動特性進行了較為深入的研究，但是，基于BEM與CFD兩種計算方法對風力機葉片氣動載荷的對比研究較少，且集中在兩葉片風力機或者功率較小的小型風力機。本文采用修正的BEM和不同來流條件下CFD數值模擬兩種方法研究大型風力機三維旋轉效應導致的葉尖損失、動態失速等現象，分析對比兩種風力機氣動性能計算方法，為風力機的設計、功率預測和氣動載荷的研究以及BEM的進一步修正提供理論支撐。

1 氣動性能計算方法

1.1 修正后的葉素動量理論

BEM通過對作用在葉片展向上每個微段上的力進行積分得到作用于風輪上的推力及轉矩。圖1為葉片剖面和氣流角受力關系圖。圖中：入流角φ為總速度W與風輪轉動平面的夾角，由局部攻角(α）和葉素槳距角(β）組成，變量V1為入流風速，Ω為風輪轉速，a為軸向誘導因子，b為周向誘導因子。根據作用在葉片截面上的升力(L）和阻力(D）的關系可以得到葉素上氣動合力的軸向分量和切向分量。

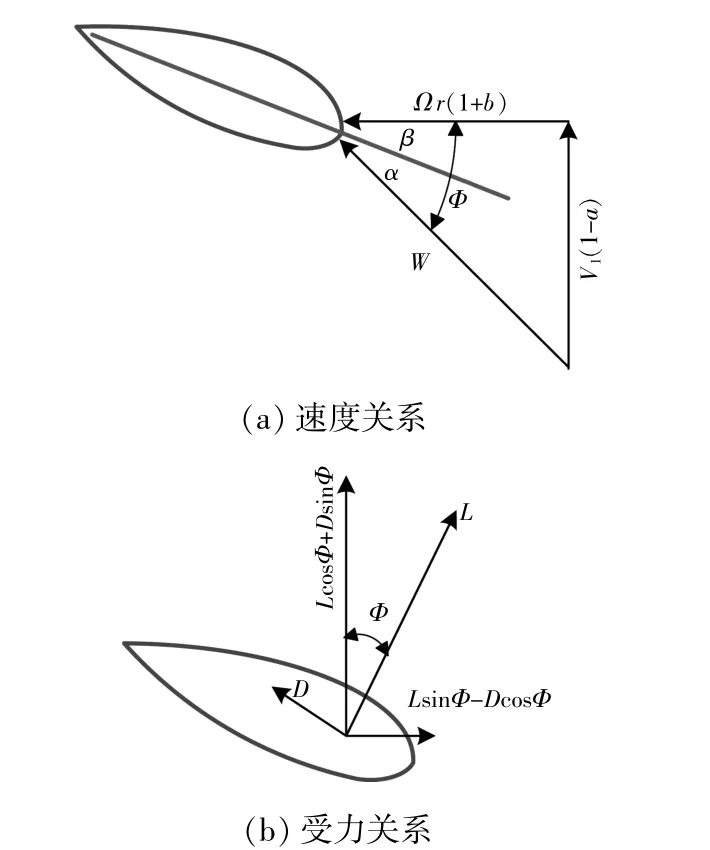
圖1 葉片剖面和氣流角受力關系Fig.1 Force relation diagram of blade profile and flow angle

作用在葉片單元上的法向力和轉矩可以通過升力系數(CL）和阻力系數(CD）的關系得到，假設葉片單元的弦長(c）已知，葉片數為N，則法向力dFA和轉矩dT可以表示為

由于模型中假設每個葉片截面與相鄰截面之間沒有相互作用，使得該模型無法捕捉葉片上發生的三維效應，尤其是在葉尖和葉根附近。此外，氣流繞風輪葉片剖面流動使得葉片表面氣流分離，進而導致梢部和根部翼型表面的環量減少，相應計算的轉矩也會減小。因此，利用BEM計算時需要考慮修正因子，通常使用文獻[7]的葉根、葉尖損失修正因子來校正剖面數據。

式中：rn為輪轂半徑；Ft為葉尖損失修正因子；Fr為葉根損失修正因子。

令葉尖葉根修正因子F=Ft?Fr，則修正后的法向力和轉矩可以表示為

文獻[8]在文獻[7]的修正因子的基礎上，引入一個新的修正項用于法向力系數Cn和切向力系數Ct，并將其代入經典的葉素理論中得到推力與轉矩。

同 理，令F′=Ft′?F′，其 中g=exp[-c1(Nλ-c2）]，c1=0.125，c2=21，則修正后的法向力和轉矩可以表示為

1.2 CFD數值模擬

1.2.1建立計算模型及網格無關性驗證

以某1.5 MW大型水平軸風力機為研究對象，選取風機葉片常用翼型S809，設計功率為1.5 MW，風 速V為12 m/s，風 輪 轉 速 為22.6 r/min，直徑D為71 m。設置內域為旋轉域，外域為靜止域，劃分非結構化四面體網格并對葉片附近以及內流域區域進行網格加密，當網格數量大于960萬時，功率誤差變化很小，因此最終確定數值計算的總網格數為960.4萬。網格無關性驗證見表1。

表1 網格無關性驗證Table 1 Validation of grid independence

將模型導入求解器中進行求解，定義湍流模型為SST k-ω，設置速度入口和壓力出口。壓力速度耦合采用SIMPLE算法，離散方式為二階迎風格式。將速度入口邊界條件以UDF的形式加載到求解器中分別進行均勻風場和非定常流動風場的風力機三維數值模擬，在葉尖和葉根處設置壓力監測點，監測葉片表面壓力隨時間的變化。壓力監測點位置如圖2所示。

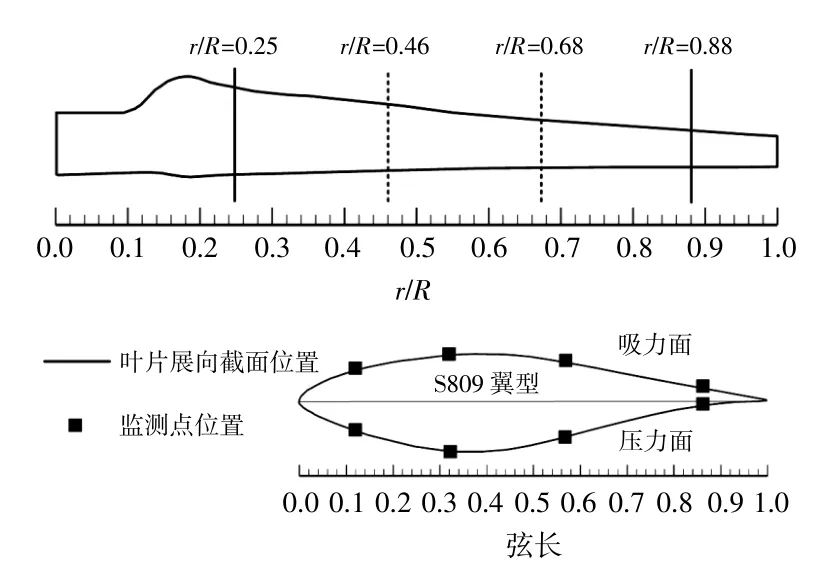
圖2 壓力監測點位置Fig.2 Location of the pressure monitoring point

1.2.2湍流風場的模擬方法

由于風力機葉片在旋轉過程中會發生流動分離、失速延遲等現象，而復雜的工作環境，例如大氣邊界層、湍流、風剪切、風速和風向的瞬變性以及偏航等會使翼型及葉片的氣動行為呈現強烈的非定常特性，目前大多數關于水平軸風力機的研究沒有考慮到這種不穩定性。

非定常流的模型復雜，模擬真實脈動風需要大量計算資源與時間，在理想情況下，可以將高頻湍流風視為均勻來流、剪切來流以及湍流，其中湍流風可以被理想化為隨時間變化的具有平均值、幅值和頻率的正弦曲線形式的風速序列。此外，文獻[9]的研究結果表明，正弦函數形式的脈動風速序列非常適合替代湍流來研究非定常流動行為，因此，本文使用式(11）表示某一局部時間點的瞬時風速。

式 中：vˉ(z）為 距 地 面 高 度z處 的 平 均 風 速；k為 湍流強度，為風速的標準差與平均風速之比；f為風的脈動頻率；t為流動時間。

為了突出脈動風的波動特征，對式(11）中的相應參數進行指定，來設置較高的頻率和振幅，其中f取1 Hz，k取0.1，z垂直于地面方向向上。

平均風速隨高度的變化可以用指數率分布來描述。

式 中：γ為 切 變 系 數 或 粗 糙 度 指 數，取0.27；vˉ(z0）為距地面高度z0=10 m處的平均風速，取6.4 m/s。

2 結果與討論

2.1 翼型氣動性能分析

在進行三維數值模擬前，先分析S809翼型的氣動性能，以驗證湍流模型的準確性，俄亥俄州立大學(OSU）對翼型S809進行了不同雷諾數條件下的風洞試驗[10]。本文為了改善失速狀態下數值模擬的準確性，在均勻來流條件下使用SST k-ω湍流模型，選取封閉常數 β*作為調整參數。β*會改變湍動能k和湍流耗散率ω，在翼型數值模擬中校正湍流模型的封閉常數并用于葉片的數值模擬。獲得不同攻角(α）下翼型的CL和CD，并將仿真結果與OSU的二維靜態測試數據和BEM計算結果進行對比(圖3）。

圖3 不同攻角下翼型升力系數對比Fig.3 Comparison of airfoil lift coefficients at different angles of attack

由圖3可知：在 α為0～8 °時，CL呈線性增長，在 α為8～16°時，CL趨于平緩，在 α超過16°后，CL急劇下降，調整封閉參數后的CFD模擬結果和實驗數據幾乎完全吻合；在α>8°時，BEM計算結果與CFD模擬結果和實驗結果差異較大，表明BEM不能很好地預測翼型在失速狀態下的氣動性能，需要進一步修正。

圖4為不同 α下的翼型流線圖。由圖4可知，隨著 α的增大，失速區域逐漸增大且分離點逐漸向前緣移動，可將3個階段稱為附著流動狀態(α為0～8°）、輕 失 速 狀 態(α為8～16°）和 深 度失 速 狀 態(α>16°）。

圖4 不同攻角下翼型流線圖Fig.4 Flow diagram of airfoil at different angles of attack

2.2 葉片表面極限流線圖

圖5為均勻來流條件下不同葉尖速比(TSR）下的極限流線。當風速分別為12，14，16.8 m/s和21 m/s時，對 應 的TSR分 別 為7，6，5和4。在 離 心力和葉片展向壓力梯度的作用下，氣流在葉根處發生分離并沿葉片展向流動，展向壓力梯度隨著攻角和葉尖速比的變化而變化。

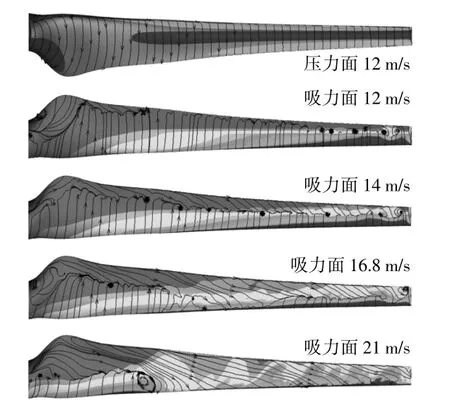
圖5 葉片表面極限流線Fig.5 Limiting streamline of blade surface

由圖5可知：當風速為12 m/s時，所有流線均從前緣指向后緣，葉片壓力面均為附著流動，沒有發生失速，除葉根小部分區域外，葉片吸力面基本未發生分離流動；隨著風速的增加，葉根部位分離點向前緣移動，葉片吸力面分離區域逐漸增大，葉片展向有明顯的流動分離線；當風速增大到21 m/s時，葉片處于深度失速狀態，吸力面流動完全分離，沿葉片展向有速度分量，在靠近葉根部位產生一個較大的氣流漩渦。

2.3 葉片表面壓力頻譜特性分析

為了進一步研究非定常來流對風力機葉片表面壓力波動的影響，對各葉尖和葉根部位截面監測點所測壓力進行FFT變換，得到壓力功率譜(圖6）。壓力功率譜總體上符合Kolmogorov-5/3功率定律，所有截面在頻率f=0.376 Hz時均出現明顯的峰值，而且該頻率與風輪的旋轉頻率相等，風輪的旋轉頻率fn=n/60(n為風輪轉速），說明壓力脈動的主頻為1倍風輪轉動頻率，即f=1fn。

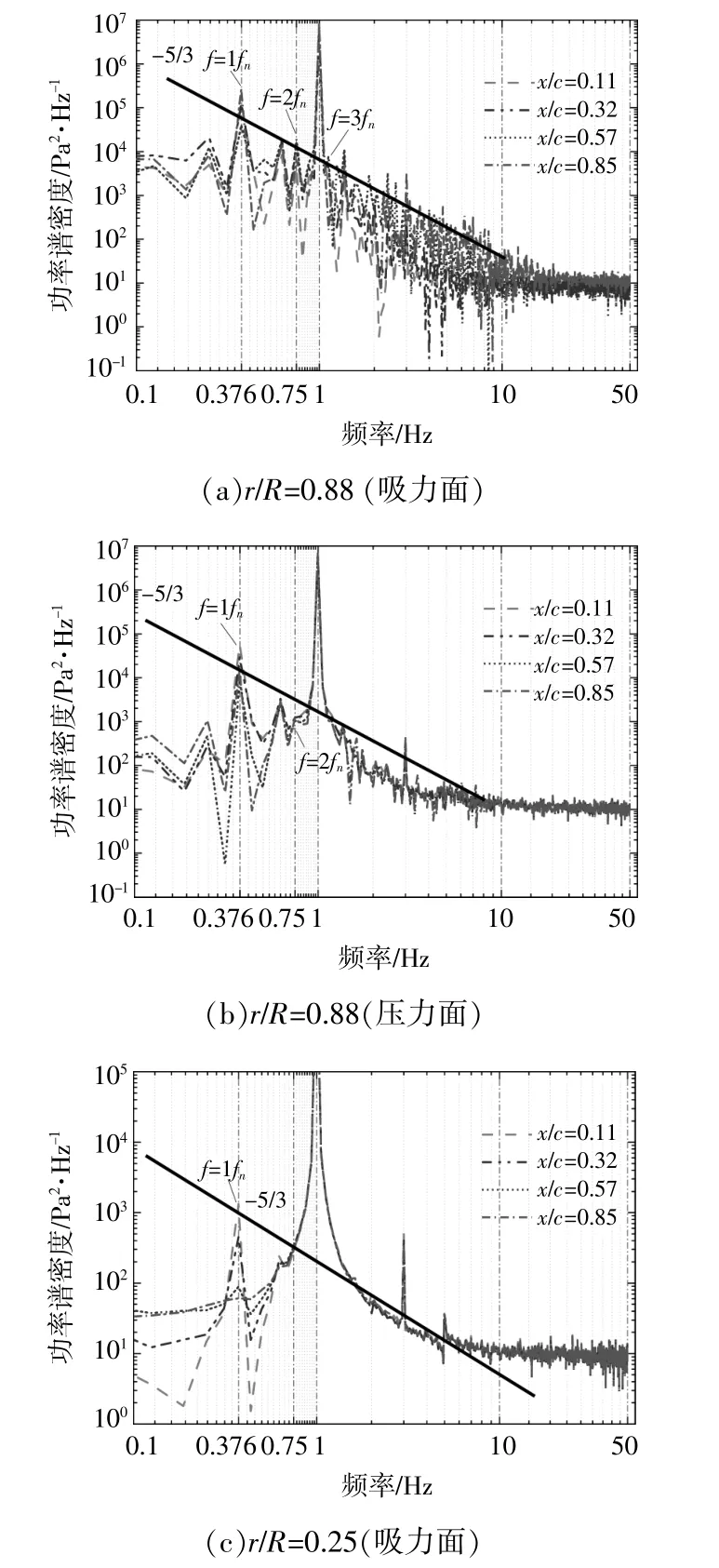
圖6 翼型壓力的功率譜特性Fig.6 Power spectrum characteristics of airfoil pressure

由圖6(a）可知：當f=1fn時，所有測點壓力功率譜均出現明顯的峰值，峰值從大到小依次是x/c等 于0.85，0.11，0.32和0.57，靠 近 后 緣 的x/c為0.85時的功率譜峰值最大，說明葉片后緣壓力含有的主頻能量最高；在高頻段，靠近尾緣的x/c=0.85呈現明顯的鋸齒狀分布特性，其余所有壓力功率譜均呈現紊亂狀態，表明葉尖部位翼型吸力面對失速旋渦的敏感程度較高，尤其是尾緣部位。

由圖6(b）可知：當f=1fn時，所有測點壓力功率譜均出現明顯的峰值，峰值從大到小依次是x/c等于0.11，0.32，0.85和0.57，最接近前緣的x/c等于0.11的功率譜峰值最大，表明前緣對來流最敏感，后緣次之而翼型中部最弱；在頻率f為2～11 Hz時，功率譜峰值點不明顯，表明葉尖部位翼型壓力面對失速旋渦的敏感程度較低。

由于葉根部位翼型受轉頻影響較小，使得葉根在2～5倍轉頻的功率譜峰值不明顯[圖6(c），(d）]，但總體上符合Kolmogorov-5/3功率定律。

總體而言，壓力功率譜在高頻段均呈現相對平緩的變化趨勢，而且壓力面壓力功率譜的平緩變化趨勢更明顯，翼型越接近葉根，平緩變化的功率譜所占頻段越寬；由于靠近葉根翼型的攻角較大，吸力面受到順壓梯度作用較強，流動分離嚴重，使得吸力面靠近葉根部位的功率譜的平緩變化區域較小。

2.4 BEM與CFD葉片載荷預測結果對比

本文使用QBlade進行BEM計算來預測葉片氣動載荷，考慮了失速延遲效應的影響，分別利用兩種修正方法對BEM進行修正并將修正后的結果與CFD計算結果進行對比。將葉片弦長、扭角等參數導入到QBlade中完成葉片模型的建立并進行氣動性能分析，然后與文獻[11]中的CFD模擬計算結果進行對比(圖7）。

圖7 葉片截面力對比Fig.7 Comparison of blade cross section force

由圖7可知：兩種不同風力機模型計算得到的氣動載荷趨勢一致，沿著展向葉片所受Fn逐漸增大，葉尖損失的存在使得在接近葉尖時Fn和Ft均有所減小，同時也從側面證明了本文葉片設計與計算結果的合理性；Fn和Ft在葉根處修正后的BEM與原始的BEM計算結果差別不大，而在葉尖處修正過后更加接近CFD模擬結果；相較于文獻[7]修正的BEM，文獻[8]修正的BEM對于Fn的預測更加準確，對于Ft，二者預測結果差別不大。整體而言，修正后的BEM能夠較好地預測出氣動載荷隨著葉片展向位置變化的趨勢，但是與CFD計算結果相比仍存在一定偏差。

3 結論

本文采用修正的BEM和三維CFD數值模擬兩種計算方法分析預測了1.5 MW風力機的氣動性能。考慮了葉尖損失、失速延遲效應以及均勻來流和非穩態來流兩種流動風場。研究正弦振蕩和剪切流場下由風力機三維旋轉效應產生的流動分離和動態失速效應，分析了脈動風條件下葉片表面壓力頻譜特性，最后利用QBlade軟件建立優化設計的風力機模型，將計算結果與CFD模擬結果進行對比，得出以下結論。

①標準狀況下，葉片表面基本為附著流動，在葉根和葉尖會產生分離渦。隨著風速的增加，在離心力和葉片展向壓力梯度的作用下，葉片吸力面開始發生流動分離，深失速區域逐漸增大，風速增大到21 m/s時，吸力面氣流完全分離。

②通過葉片展向上不同位置截面壓力功率譜可以看出，測點壓力在1倍風輪轉頻時出現峰值且前緣峰值最高，由于葉尖渦的影響，葉尖吸力面后緣峰值最高；葉尖部位翼型截面吸力面對失速旋渦的敏感程度較高，壓力面敏感程度較低，葉根部位翼型受轉頻影響較小。